Ma trận chuyển vị

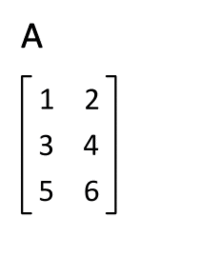
Trong đại số tuyến tính, ma trận chuyển vị (tiếng Anh: transpose) là ma trận mà các hàng được đổi thành các cột và ngược lại. Để tính toán ma trận chuyển vị, ta sử dụng toán tử chuyển vị theo đường chéo chính. Ký hiệu của ma trận chuyển vị của ma trận A là A.

Ma trận chuyển vị được nhà toán học người Anh Arthur Cayley giới thiệu vào năm 1858.

Chuyển vị của ma trận

Khái niệm

Chuyển vị của ma trận A, ký hiệu là A^T, có thể được xây dựng bằng các phương pháp sau đây:

1. Phản chiếu A qua đường chéo chính (chạy từ trên cùng bên trái sang dưới cùng bên phải) để có A^T;
2. Viết các hàng của A thành cột của A^T;
3. Viết các cột của A thành hàng của A^T.

Về mặt lý thuyết, phần tử ở hàng thứ i, cột thứ j của ma trận A sẽ trở thành phần tử ở hàng thứ j, cột thứ i của ma trận A^T:

${\left[A^{⊺}\right]}_{ij}={\left[A\right]}_{ji}.$

Nếu A là ma trận có kích thước m × n thì A^T là ma trận có kích thước n × m.

Trong trường hợp ma trận vuông, A^T biểu thị chuyển vị của ma trận A. Để tránh nhầm lẫn, nhiều tác giả sử dụng ký hiệu lũy thừa T bên trái, khi đó ký hiệu chuyển vị là A^T. Một lợi thế của ký hiệu này là không cần dấu ngoặc khi liên quan đến số mũ: ví dụ, (A^T)² không gây nhầm lẫn.

Trong bài viết này, để tránh nhầm lẫn, sẽ không sử dụng ký hiệu T dưới dạng tên biến.

Ma trận vuông có chuyển vị bằng chính nó được gọi là ma trận đối xứng; nghĩa là, A đối xứng nếu A = A^T.

$A^T=A.$

Ma trận vuông có chuyển vị bằng phần trừ của nó được gọi là ma trận phản đối xứng; nghĩa là, A phản đối xứng nếu

$A^T=-A.$

Ma trận vuông phức có chuyển vị bằng ma trận với mỗi phần tử được thay thế bằng liên hợp phức của nó được gọi là ma trận Hermitian (tương đương với ma trận bằng chuyển vị liên hợp); nghĩa là, A là Hermitian nếu

$A^T=\overline{A}.$

Ma trận vuông phức có chuyển vị là phủ định của liên hợp phức của nó được gọi là ma trận phản Hermitian; nghĩa là, A là phản Hermitian nếu

$A^T=-\overline{A}.$

Ma trận vuông có chuyển vị bằng nghịch đảo của nó được gọi là ma trận trực giao; nghĩa là, A là ma trận trực giao nếu

$A^T=A^{-1}.$

Một ma trận phức vuông có chuyển vị bằng nghịch đảo liên hợp của nó được gọi là ma trận unita; nghĩa là, A là ma trận unita nếu

$A^T=\overline{A^{-1}}.$

Ví dụ

Các tính chất

Cho A và B là hai ma trận và c là một số vô hướng.

Tính chất của ma trận chuyển vị

Nếu A là một ma trận kích thước m × n và A là chuyển vị của nó, thì tích của phép nhân ma trận giữa A và A sẽ tạo ra hai ma trận vuông: A A là ma trận kích thước m × m và A A là ma trận kích thước n × n. Hơn nữa, cả hai ma trận này đều là ma trận đối xứng. Đúng vậy, ma trận A A có các phần tử là tích trong của một hàng của A với một cột của A. Do các cột của A chính là các hàng của A, nên phần tử tương ứng với tích trong của hai hàng của A sẽ là đối xứng. Nếu phần tử p_{i j} được lấy từ hàng i và j của A, thì phần tử p_{j i} cũng lấy từ cùng hàng, do đó p_{i j} = p_{j i}, chứng tỏ rằng ma trận (p_{i j}) là đối xứng. Tương tự, ma trận A A cũng là một ma trận đối xứng.

Một cách nhanh chóng để chứng minh tính đối xứng của A A là dựa vào thực tế rằng nó chính là chuyển vị của chính nó:

${\left(A{A}^T\right)}^T={\left(A^T\right)}^T{A}^T=A{A}^T.$

Thực hiện chuyển vị ma trận trên máy tính

Trên máy tính, để tránh việc chuyển vị ma trận trong bộ nhớ, người ta thường chỉ cần truy cập dữ liệu theo một thứ tự khác. Ví dụ, các thư viện phần mềm đại số tuyến tính như BLAS thường cung cấp tùy chọn cho phép diễn giải một số ma trận theo thứ tự hoán vị, nhằm tránh việc di chuyển dữ liệu.

Tuy nhiên, có những tình huống cần hoặc muốn sắp xếp lại một ma trận vật lý trong bộ nhớ theo thứ tự hoán vị của nó. Ví dụ, khi ma trận được lưu theo hàng, các hàng của ma trận sẽ liền nhau trong bộ nhớ, trong khi các cột không liền nhau. Nếu các thao tác cần thực hiện liên tục trên các cột, như trong thuật toán biến đổi Fourier nhanh, việc hoán vị ma trận trong bộ nhớ (để các cột liền nhau) có thể cải thiện hiệu suất bằng cách giảm thời gian truy cập.

Lý tưởng nhất, chúng ta muốn thực hiện việc hoán vị ma trận với lượng bộ nhớ bổ sung tối thiểu. Điều này dẫn đến việc hoán vị một ma trận kích thước n × m với bộ nhớ bổ sung O(1) hoặc ít hơn nhiều so với mn. Khi n ≠ m, việc này đòi hỏi một hoán vị phức tạp của các phần tử dữ liệu, không dễ thực hiện tại chỗ. Vì vậy, việc hoán vị ma trận tại chỗ hiệu quả đã trở thành chủ đề nghiên cứu trong lĩnh vực khoa học máy tính từ cuối những năm 1950, và nhiều thuật toán đã được phát triển.

Hoán vị của ánh xạ tuyến tính và dạng song tuyến tính

Nhớ rằng ma trận có thể được ánh xạ 1-1 với các toán tử tuyến tính. Hoán vị của một toán tử tuyến tính có thể được xác định mà không cần phải biểu diễn ma trận. Điều này dẫn đến một định nghĩa tổng quát hơn về phép hoán vị có thể áp dụng cho các toán tử tuyến tính không thể biểu diễn bằng ma trận (như các không gian vectơ vô hạn chiều).

Hoán vị của ánh xạ tuyến tính

Xét X là không gian đối ngẫu đại số (algebraic dual space) của một mô-đun-R- X. Giả sử X và Y là các mô-đun-R. Nếu u : X → Y là một ánh xạ tuyến tính, thì phần phụ đại số (algebraic adjoint) hoặc đối ngẫu (dual) của nó là ánh xạ u : Y → X được xác định bởi f ↦ f ∘ u. Hàm kết quả u(f) được gọi là pullback của f qua u. Mối quan hệ sau đặc trưng cho phần phụ đại số của u

⟨u(f), x⟩ = ⟨f, u(x)⟩ với mọi f ∈ Y' và x ∈ X

trong đó ⟨•, •⟩ là một hệ đối ngẫu (dual system) (tức là được xác định bởi ⟨z, h⟩ := h(z)). Định nghĩa này cũng áp dụng cho mô-đun bên trái và không gian vectơ mà không thay đổi.

Định nghĩa của phép hoán vị có thể được coi là độc lập với bất kỳ dạng song tuyến nào trên các mô-đun, khác với phần phụ (dưới đây).

Không gian đối ngẫu liên tục của một không gian vectơ tôpô (TVS) X được ký hiệu là X'. Nếu X và Y là các không gian vectơ tôpô, thì một ánh xạ tuyến tính u : X → Y được gọi là liên tục yếu khi và chỉ khi u(Y') ⊆ X'. Trong trường hợp này, ánh xạ u : Y' → X' thể hiện sự hạn chế của u tới Y'. Ánh xạ u được gọi là chuyển vị của u.

Nếu ma trận A biểu diễn một ánh xạ tuyến tính đối với cơ sở của V và W, thì ma trận A cũng biểu diễn chuyển vị của ánh xạ tuyến tính đó đối với cơ sở đối ngẫu (dual base).

Chuyển vị của một dạng song tuyến tính

Mọi ánh xạ tuyến tính đến không gian đối ngẫu u : X → X định nghĩa một dạng song tuyến B : X × X → F, với mối quan hệ B(x, y) = u(x)(y). Nếu chuyển vị của dạng song tuyến này được xác định là dạng song tuyến B bởi chuyển vị của u : X → X, tức là B(y, x) = u(Ψ(y))(x), thì ta có B(x, y) = B(y, x). Ở đây, Ψ là phép đồng cấu tự nhiên X → X vào đôi liên hiệp.

Phần phụ

Khi không gian vectơ X và Y có các dạng song tuyến tính không suy biến lần lượt là B_X và B_Y, thì khái niệm phần phụ—liên quan mật thiết đến chuyển vị—có thể được định nghĩa như sau:

Nếu u : X → Y là một ánh xạ tuyến tính giữa các không gian vectơ X và Y, thì g được gọi là phần phụ của u nếu tồn tại ánh xạ g : Y → X sao cho:

với mọi x ∈ X và y ∈ Y.

Các dạng song tuyến tính này xác định đẳng cấu giữa X và X, cũng như giữa Y và Y, dẫn đến sự đẳng cấu giữa chuyển vị và phần phụ của u. Ma trận của phần phụ tương đương với ma trận chuyển vị khi cơ sở là trực chuẩn đối với dạng song tuyến. Trong ngữ cảnh này, thuật ngữ chuyển vị đôi khi được dùng để chỉ phần phụ theo định nghĩa này.

Phần phụ cho phép xác định liệu g : Y → X có tương đương với u : Y → X hay không. Điều này đặc biệt quan trọng vì nó cho phép xác định nhóm trực chuẩn trên không gian vectơ X với dạng bậc hai mà không cần dựa vào ma trận (hoặc các thành phần của nó), thông qua tập hợp tất cả các ánh xạ tuyến tính X → X mà phần phụ tương ứng là nghịch đảo.

Trong một không gian vectơ phức tạp, thường sử dụng dạng bán song tuyến (tuyến tính liên hợp trong một đối số) thay vì dạng song tuyến. Phần phụ Hermitian của ánh xạ giữa các không gian như vậy được xác định tương tự, và ma trận của phần phụ Hermitian là ma trận chuyển vị liên hiệp nếu các cơ sở là trực chuẩn.

• Ma trận phụ hợp, chuyển vị của định thức con
• Chuyển vị liên hiệp
• Giả nghịch đảo Moore–Penrose
• Phép chiếu (đại số tuyến tính)

Xem thêm

• Bản mẫuAlgebra I Chapters 1-3 Springer
• Halmos, Paul (1974), Finite dimensional vector spaces, Springer, ISBN 978-0-387-90093-3.
• Maruskin, Jared M. (2012). Essential Linear Algebra. San José: Solar Crest. tr. 122–132. ISBN 978-0-9850627-3-6.
• Bản mẫuWolff Topological Vector Spaces
• Bản mẫuèves François Topological vector spaces, distributions and kernels
• Schwartz, Jacob T. (2001). Introduction to Matrices and Vectors. Mineola: Dover. tr. 126–132. ISBN 0-486-42000-0.

Các liên kết bên ngoài

• Gilbert Strang (Mùa xuân 2010) Đại số tuyến tính từ MIT Open Courseware