Ma trận có thể được chéo hóa

Trong đại số tuyến tính, một ma trận vuông được gọi là chéo hóa được hoặc không khiếm khuyết nếu nó tương đương với một ma trận đường chéo. Cụ thể, tồn tại một ma trận khả nghịch và một ma trận đường chéo sao cho [ P^{-1}AP = D ] hoặc [ A = PDP^{-1} ]. Lưu ý rằng ma trận P và D không phải là duy nhất. Đối với một không gian vectơ hữu hạn chiều, một biến đổi tuyến tính được gọi là chéo hóa được nếu có thể tìm được một cơ sở của không gian với các vectơ riêng của biến đổi đó. Nếu ma trận của biến đổi tuyến tính được viết dưới dạng [ A = PDP^{-1} ], thì các vectơ cột của P là cơ sở của không gian các vectơ riêng và các phần tử trên đường chéo của ma trận D là các giá trị riêng của biến đổi tuyến tính.

Từ góc nhìn hình học, một ma trận chéo hóa được có thể coi là một phép giãn không đồng nhất (hay phép co giãn dị hướng), vì nó giãn các vectơ trong không gian theo cách giống như phép giãn đồng nhất, nhưng với hệ số khác nhau cho mỗi trục vectơ riêng, mà hệ số đó được xác định bởi giá trị riêng tương ứng.

Chéo hóa là quá trình xác định các ma trận P và D sao cho ma trận có thể được biểu diễn dưới dạng chéo. Sau khi tìm được các giá trị riêng và vectơ riêng, việc tính toán với ma trận chéo trở nên rất đơn giản. Ví dụ, việc nâng ma trận chéo D lên lũy thừa bất kỳ chỉ cần nâng từng phần tử trên đường chéo lên lũy thừa tương ứng, và định thức của ma trận chéo là tích của các phần tử trên đường chéo. Điều này cũng áp dụng cho ma trận A khi biểu diễn dưới dạng [ A = PDP^{-1} ].

Một ma trận vuông không chéo hóa được được gọi là khiếm khuyết. Có thể xảy ra tình huống một ma trận có các phần tử số thực không chéo hóa được trên trường số thực, tức là không tồn tại ma trận P khả nghịch và D chéo với các phần tử số thực sao cho [ A = PDP^{-1} ]. Tuy nhiên, trên trường số phức, ma trận có thể chéo hóa được. Ví dụ, ma trận của phép quay thường là một trường hợp như vậy.

Định nghĩa

Một ma trận vuông kích thước $A$ cỡ $n\times <!--\; \times \; -->n$ trên một trường $F$ được gọi là có thể chéo hóa hoặc không khiếm khuyết nếu có một ma trận khả nghịch $P$ sao cho $P^{-<!--\; -\; -->1}AP$ là ma trận đường chéo. Đây là một định nghĩa chính xác.

$A\in <!--\; \in \; -->F^{n\times <!--\; \times \; -->n}\text{ chéo hóa được}⟺<!--\; ⟺\; -->\mathrm{\exists <!--\; \exists \; -->}P,P^{-<!--\; -\; -->1}\in <!--\; \in \; -->F^{n\times <!--\; \times \; -->n}:P^{-<!--\; -\; -->1}AP\text{ là đường chéo}$

Đặc tính

Dưới đây là một số điểm cơ bản về ma trận và các biến đổi có thể được chéo hóa:

• Một ma trận $A$ kích thước $n\times <!--\; \times \; -->n$ trên trường $F$ có thể được chéo hóa khi và chỉ khi tổng số chiều của các không gian con riêng của nó bằng $n$, tức là khi và chỉ khi tồn tại một cơ sở của $F^n$ gồm các vectơ riêng của $A$. Nếu một cơ sở như vậy có thể được tìm thấy, ta có thể xây dựng ma trận $P$ với các vectơ cơ sở làm cột, và ma trận $P^{-<!--\; -\; -->1}AP$ sẽ trở thành ma trận đường chéo với các phần tử trên đường chéo là các giá trị riêng của $A$. Ma trận $P$ giúp chuyển cơ sở và được gọi là ma trận modal của $A$.
• Biến đổi tuyến tính $T:V\to <!--\; \to \; -->V$ có thể được chéo hóa khi và chỉ khi tổng số chiều của các không gian con riêng của nó bằng $\dim <!--\; \; -->\left(V\right)$, tức là khi và chỉ khi tồn tại một cơ sở của $V$ bao gồm các vectơ riêng của $T$. Với một cơ sở như vậy, $T$ sẽ được biểu diễn bởi ma trận đường chéo, trong đó các phần tử trên đường chéo là các giá trị riêng của $T$.

Một đặc điểm quan trọng nữa là: Một ma trận hoặc biến đổi tuyến tính có thể chéo hóa trên trường $F$ nếu và chỉ nếu đa thức tối tiểu của nó có thể phân tích thành tích của các nhân tử tuyến tính phân biệt trên $F$. (Nói cách khác, một ma trận có thể chéo hóa khi và chỉ khi tất cả các ước nguyên sơ của nó là các yếu tố tuyến tính.)

Một điều kiện đủ nhưng không cần thiết, rất hữu ích trong thực tế là:

Nếu ma trận $A$ trên trường $F$ có thể chéo hóa, thì mọi lũy thừa của ma trận đó cũng có thể được chéo hóa.

Nhiều kết quả về ma trận chéo hóa chỉ đúng trên các trường đại số đóng như trường số phức. Trong những trường hợp này, tập hợp các ma trận có thể chéo hóa là trù mật trong không gian ma trận, tức là mỗi ma trận không chéo hóa được có thể trở thành ma trận chéo hóa được với một biến đổi nhỏ. Định lý chuẩn tắc Jordan cho biết rằng mỗi ma trận có thể phân tích thành tổng duy nhất của một ma trận chéo hóa được và một ma trận lũy linh. Trên trường đại số đóng, các ma trận chéo hóa được đồng nhất với các ma trận nửa đơn.

Chéo hóa

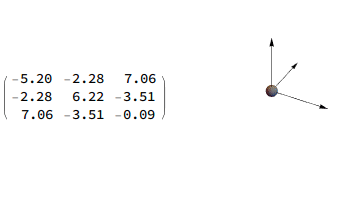
Nếu ma trận $A$ có thể chéo hóa, có nghĩa là

Vậy có:

Khi viết ma trận $P$ dưới dạng các khối gồm các vectơ cột của nó

Phương trình trên có thể được diễn đạt dưới một dạng khác

$A{\stackrel{\to <!--\; \to \; -->}{\mathrm{\alpha <!--\; \alpha \; -->}}}_i={\mathrm{\lambda <!--\; \lambda \; -->}}_i{\stackrel{\to <!--\; \to \; -->}{\mathrm{\alpha <!--\; \alpha \; -->}}}_i(i=1,2,\cdots <!--\; \cdots \; -->,n).$

Vì vậy, các vectơ cột của $P$ là các vectơ riêng bên phải của $A$ (trong khi các vectơ hàng của $P^{-<!--\; -\; -->1}$ là các vectơ riêng bên trái). Các giá trị trên đường chéo của $P$ tương ứng với các giá trị riêng của chúng. Vì $P$ có thể đảo ngược, các vectơ riêng là độc lập tuyến tính và tạo thành một cơ sở của

$F^n$. Đây là điều kiện cần và đủ để thực hiện phép chéo hóa và là cách chính để thực hiện việc chéo hóa: tức là ta biểu diễn $A$ theo cơ sở riêng của nó.

Khi một ma trận phức $A\in <!--\; \in \; -->C^{n\times <!--\; \times \; -->n}$ là ma trận Hermite (hoặc tổng quát hơn, ma trận chuẩn tắc), thì các vectơ riêng của $A$ có thể được chọn sao cho tạo thành một cơ sở trực chuẩn của $C^n$. Khi đó, $P$ có thể chọn là ma trận đơn vị. Nếu $A\in <!--\; \in \; -->R^{n\times <!--\; \times \; -->n}$ là ma trận đối xứng thực, thì các vectơ riêng của nó có thể được chọn để tạo thành một cơ sở trực chuẩn của $R^n$ và $P$ có thể chọn là ma trận trực giao.

Để thực hiện việc chéo hóa ma trận trong thực tiễn, thường sử dụng phần mềm máy tính. Nhiều thuật toán đã được phát triển để hỗ trợ quy trình này.

Chéo hóa đồng thời

Một tập hợp các ma trận được coi là chéo hóa đồng thời nếu có một ma trận khả nghịch duy nhất $P$ sao cho $P^{-<!--\; -\; -->1}AP$ là ma trận chéo cho mọi ma trận $A$ trong tập. Định lý sau đây chỉ ra rằng một tập hợp các ma trận có thể chéo hóa đồng thời khi và chỉ khi chúng giao hoán với nhau.

Các ma trận $n\times <!--\; \times \; -->n$ trên $C$ với $n>1$ không luôn có thể chéo hóa đồng thời. Ví dụ, hai ma trận

đều có thể được chéo hóa riêng lẻ nhưng không thể chéo hóa đồng thời vì chúng không giao hoán.

Một tập hợp các ma trận chuẩn tắc sẽ giao hoán với nhau khi và chỉ khi chúng có thể được chéo hóa đồng thời bằng một ma trận unita; cụ thể, tồn tại một ma trận unita $U$ sao cho $U^{\ast <!--\; \ast \; -->}AU$ là ma trận chéo đối với mọi ma trận $A$ trong tập hợp.

Ví dụ

Ma trận có thể chéo hóa

Ma trận không thể chéo hóa

Ma trận quay thường không thể chéo hóa trên tập hợp các số thực nhưng có thể thực hiện việc chéo hóa trên tập hợp các số phức.

Một số ma trận không thể chéo hóa trên bất kỳ trường số nào, đặc biệt là các ma trận lũy linh khác không. Hiện tượng này thường xảy ra khi số bội đại số không bằng số bội hình học của một giá trị riêng.

Dù một ma trận không thể chéo hóa, ta vẫn có thể tìm dạng chuẩn tắc Jordan của nó.

Có những ma trận thực không thể chéo hóa trên trường số thực. Ví dụ là ma trận đối xứng chéo dưới đây

Ma trận $B$ không có giá trị riêng thực, do đó không thể tìm ma trận khả nghịch thực $Q$ sao cho $Q^{-<!--\; -\; -->1}BQ$ là ma trận chéo. Tuy nhiên, nếu cho phép sử dụng số phức, ta có thể thực hiện việc chéo hóa ma trận $B$.

Vậy $Q^{-<!--\; -\; -->1}BQ$ trở thành ma trận chéo. Ta thấy rằng B đại diện cho phép quay ngược chiều kim đồng hồ một góc $\mathrm{\theta <!--\; \theta \; -->}=\frac{3\mathrm{\pi <!--\; \pi \; -->}}{2}$.

Phương pháp chéo hóa một ma trận

Quá trình chéo hóa ma trận tương tự như việc xác định các giá trị riêng và vectơ riêng của nó, nếu các vectơ riêng tạo thành một cơ sở. Ví dụ, xem xét ma trận

Các nghiệm của đa thức đặc trưng $p\left(\mathrm{\lambda <!--\; \lambda \; -->}\right)=det(\mathrm{\lambda <!--\; \lambda \; -->}I-<!--\; -\; -->A)$ chính là các giá trị riêng ${\mathrm{\lambda <!--\; \lambda \; -->}}_1=1,{\mathrm{\lambda <!--\; \lambda \; -->}}_2=1,{\mathrm{\lambda <!--\; \lambda \; -->}}_3=2$. Giải hệ phương trình tuyến tính $(I-<!--\; -\; -->A)\left(v\right)=0$ cho ta các vectơ riêng $v_1=(1,1,0)$ và $v_2=(0,2,1)$, trong khi hệ phương trình $(2I-<!--\; -\; -->A)\left(v\right)=0$ cho $v_3=(1,0,-<!--\; -\; -->1)$; tức là $A\left(v_i\right)={\mathrm{\lambda <!--\; \lambda \; -->}}_i{v}_i$ với $i=1,2,3$. Những vectơ này tạo thành một cơ sở của $V=R^3$, vì vậy ta có thể sắp xếp chúng thành các cột của một ma trận chuyển cơ sở $P$ để có:

Phương trình này có thể được hiểu là: $P$ chuyển đổi từ cơ sở chuẩn tắc sang cơ sở riêng: $P\left(e_i\right)=v_i$, do đó ta có:

$P^{-<!--\; -\; -->1}AP\left(e_i\right)=P^{-<!--\; -\; -->1}A\left(v_i\right)=P^{-<!--\; -\; -->1}\left({\mathrm{\lambda <!--\; \lambda \; -->}}_i{v}_i\right)={\mathrm{\lambda <!--\; \lambda \; -->}}_i{e}_i,$

Khi ma trận $P^{-<!--\; -\; -->1}AP$ có các vectơ cơ sở chuẩn tắc là vectơ riêng của nó, đây là đặc điểm định nghĩa của ma trận $D$.

Lưu ý rằng không có yêu cầu về thứ tự của các cột vectơ riêng trong $P$; việc đổi chỗ các vectơ riêng trong $P$ chỉ làm thay đổi thứ tự của các giá trị riêng trong dạng chéo của $A$.

Ứng dụng trong hàm ma trận

Chéo hóa có thể được sử dụng để tính toán nhanh lũy thừa của một ma trận $A=PD{P}^{-<!--\; -\; -->1}$:

Cách này rất thuận tiện vì chỉ yêu cầu tính lũy thừa của ma trận chéo. Ví dụ, với ma trận $A$ có các giá trị riêng là $\mathrm{\lambda <!--\; \lambda \; -->}=1,1,2$, ta có thể tính toán như sau:

Cách tiếp cận này có thể được mở rộng cho hàm mũ ma trận và các hàm ma trận khác có thể được định nghĩa thông qua chuỗi lũy thừa. Chẳng hạn, định nghĩa hàm $\exp <!--\; \; -->\left(A\right)=I+A+\frac{1}{2!}{A}^2+\frac{1}{3!}{A}^3+\cdots <!--\; \cdots \; -->$, có thể được viết lại như sau:

Việc này rất quan trọng để xác định các biểu thức đóng rõ ràng cho các số hạng trong dãy số đệ quy tuyến tính, chẳng hạn như dãy Fibonacci.

Ứng dụng cụ thể

Xem xét ma trận sau đây:

Tính các lũy thừa của $M$ cho thấy một quy luật thú vị:

Hiện tượng này có thể được lý giải thông qua việc chéo hóa $M$. Để thực hiện điều này, cần một cơ sở của $R^2$ bao gồm các vectơ riêng của $M$. Một cơ sở như vậy được cho bởi

trong đó e_i biểu thị cơ sở chuẩn của R. Ma trận chuyển cơ sở nghịch đảo được cho bởi

$e_1=u,e_2=v-<!--\; -\; -->u.$

Kết quả tính toán trực tiếp cho thấy

$Mu=au,Mv=bv.$

Do đó, a và b chính là các giá trị riêng ứng với u và v. Theo tính chất của phép nhân ma trận, ta có

$M^{n}u=a^{n}u,M^{n}v=b^{n}v.$

Khi quay lại cơ sở chuẩn tắc, chúng ta có

Các mối liên hệ trên có thể được biểu diễn dưới dạng ma trận như sau

Như vậy, chúng ta đã giải thích được hiện tượng này.

Chéo hóa trong cơ học lượng tử

Trong cơ học lượng tử và hóa lượng tử, việc chéo hóa ma trận là một kỹ thuật tính toán phổ biến. Điều này xuất phát từ việc phương trình Schrödinger không phụ thuộc thời gian là một bài toán giá trị riêng, mặc dù không gian mà nó hoạt động là không gian Hilbert vô hạn chiều trong nhiều trường hợp vật lý.

Một phương pháp xấp xỉ phổ biến là giảm không gian Hilbert xuống số chiều hữu hạn, sau đó phương trình Schrödinger có thể được giải quyết như một bài toán giá trị riêng đối với ma trận thực đối xứng hoặc ma trận phức Hermite. Xấp xỉ này được thiết lập thông qua nguyên lý biến phân, phù hợp với các Hamiltonian bị chặn.

Lý thuyết nhiễu loạn bậc một cũng dẫn đến bài toán giá trị riêng ma trận cho các trạng thái bị suy biến.

• Ma trận khiếm khuyết
• Ma trận tam giác
• Dạng chuẩn tắc Jordan
• Định lý phổ
• Phân tích riêng của ma trận

Ghi chú