Mê cung kề

Trong lĩnh vực Toán học và Khoa học máy tính, ma trận kề (tiếng Anh: adjacency matrix) cho một đồ thị hữu hạn G có n đỉnh là một ma trận kích thước n × n. Trong đó, các phần tử không nằm trên đường chéo chính a_ij thể hiện số cạnh nối giữa hai đỉnh i và j, còn các phần tử trên đường chéo chính a_ii là gấp đôi số khuyên tại đỉnh i, hoặc chỉ đơn giản là số khuyên tại đỉnh đó (bài viết này sử dụng cách thứ nhất, trong khi các đồ thị có hướng thường theo cách thứ hai). Mỗi đồ thị chỉ có một ma trận kề duy nhất, và các đồ thị khác nhau sẽ có các ma trận kề khác nhau. Trong trường hợp đặc biệt của đồ thị đơn giản hữu hạn, ma trận kề sẽ là ma trận (0,1) với các giá trị 0 nằm trên đường chéo chính. Nếu đồ thị là vô hướng, ma trận kề sẽ là ma trận đối xứng.

Đối với những đồ thị thưa, tức là những đồ thị có ít cạnh, thường thì người ta ưu tiên sử dụng danh sách kề vì nó tiêu tốn ít bộ nhớ hơn. Ma trận liên thuộc cũng là một dạng biểu diễn ma trận khác cho đồ thị.

Mối quan hệ giữa một đồ thị và ma trận kề của nó được nghiên cứu trong lý thuyết phổ đồ thị (spectral graph theory).

Định nghĩa

• Xem xét đồ thị G=(X, U) (có thể có hướng hoặc không)
• Giả sử tập X gồm n đỉnh và được sắp xếp theo thứ tự X={$x_{\text{1}},x_{\text{2}},...,x_{\text{n}}$}, tập U gồm n cạnh và được sắp xếp theo thứ tự U={$u_{\text{1}},u_{\text{2}},...,u_{\text{n}}$}

Quy tắc

Ma trận kề của đồ thị G, được ký hiệu là B(G), là một ma trận nhị phân kích thước n x n được định nghĩa như sau: B=($B_{\text{ij}}$) với:

• B=($B_{\text{ij}}$ = 1 nếu có cạnh nối $x_{\text{i}}$ tới $x_{\text{j}}$
• B=($B_{\text{ij}}$ = 0 nếu không có cạnh nối $x_{\text{i}}$ tới $x_{\text{j}}$

Nếu G là đồ thị vô hướng, ma trận liên thuộc của nó, ký hiệu A(G), là ma trận nhị phân kích thước nxm được định nghĩa như sau: A=($A_{\text{ij}}$)

• A=($A_{\text{ij}}$) = 1 nếu tồn tại cạnh nối $x_{\text{i}}$ đến $x_{\text{j}}$
• A=($A_{\text{ij}}$) = 0 nếu không có cạnh nối $x_{\text{i}}$ tới $x_{\text{j}}$

Hình thức thể hiện

Đồ thị không có hướng

Đối với đồ thị G không có hướng (gồm 7 đỉnh):

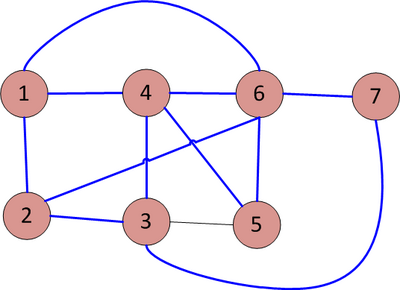
• Gọi A là ma trận kề biểu diễn đồ thị G.
• Từ đồ thị G, ta thấy:
  • 1 và 2 có cạnh nối => $A_{\text{12}}=A_{\text{21}}=1$
  • 1 và 4 có cạnh nối => $A_{\text{14}}=\; <div\; class="min-w-[250px]\; max-w-[94vw]\; md:max-w-[770px]">\; <ins\; class="adsbygoogle"\; style="display:block;\; text-align:center;"\; data-ad-layout="in-article"\; data-ad-format="fluid"\; data-ad-client="ca-pub-9247024304160346"\; data-ad-slot="4115752014"></ins>\; </div>A_{\text{41}}=1$
  • 1 và 6 có cạnh nối => $A_{\text{16}}=A_{\text{61}}=1$
  • 2 và 3 có cạnh nối => $A_{\text{23}}=A_{\text{32}}=1$
  • 2 và 6 có cạnh nối => $A_{\text{26}}=A_{\text{62}}=1$
  • 3 và 4 có cạnh nối => $A_{\text{34}}=A_{\text{43}}=1$
  • 3 và 5 có cạnh nối => $A_{\text{35}}=A_{\text{53}}=1$
  • 3 và 7 có cạnh nối => $A_{\text{37}}=A_{\text{73}}=1$
  • 4 và 6 có cạnh nối => $A_{\text{46}}=A_{\text{64}}=1$
  • 4 và 5 có cạnh nối => $A_{\text{45}}=A_{\text{54}}=1$
  • 5 và 6 có cạnh nối => $A_{\text{56}}=A_{\text{65}}=1$
  • 6 và 7 có cạnh nối => $A_{\text{67}}=A_{\text{76}}=1$
  • Còn lại các cặp đỉnh không có cạnh nối với nhau => $A_{\text{ij}}$ = $A_{\text{ji}}$ = 0
• Kết quả sau khi biểu diễn đồ thị G sang ma trận kề:

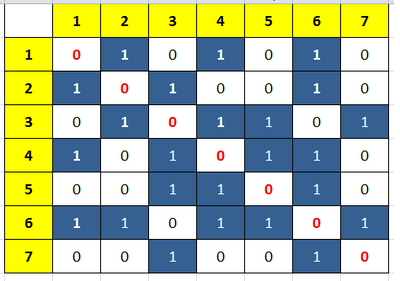
• Trong đó dòng và cột màu vàng là danh sách các đỉnh của đồ thị vô hướng G.

Biểu diễn đồ thị có hướng

Cho đồ thị G có hướng (4 đỉnh):

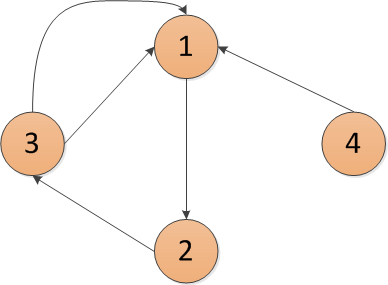
• Đặt A là ma trận kề biểu diễn đồ thị G.
• Từ đồ thị G, ta thấy:
  • 1 và 2 có 1 cạnh nối và 1 đi vào 2 => $A_{\text{12}}=1$
  • 2 và 3 có 1 cạnh nối và 2 đi vào 3 => $A_{\text{23}}=1$
  • 3 và 1 có 2 cạnh nối và 3 đi vào 1 => $A_{\text{31}}=2$
  • 4 và 1 có 1 cạnh nối và 4 đi vào 1 => $A_{\text{41}}=1$
  • Các cặp đỉnh không nối còn lại thì $A_{\text{ij}}=0$
• Kết quả khi biểu diễn đồ thị G sang ma trận kề:

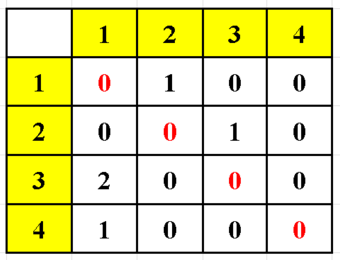
Đặc điểm

• Ma trận kề của đồ thị vô hướng là ma trận đối xứng, nghĩa là:

$a[i,j]=a[j,i],i,j=1,2,...,n.$

Ngược lại, mỗi (0,1)-ma trận đối xứng cấp n sẽ tương ứng, đúng theo cách đánh số đỉnh (hay nói cách khác: chính xác theo đẳng cấu), với một đơn đồ thị vô hướng có n đỉnh.

• Ma trận kề của đồ thị có hướng không phải là ma trận đối xứng.
• Đối với đồ thị vô hướng, tổng các phần tử trên dòng i (cột j) của ma trận kề chính là bậc của đỉnh i (đỉnh j).
• Đối với đồ thị có hướng, tổng các phần tử trên dòng i (cột i) sẽ thể hiện bán bậc ra (bán bậc vào) của đỉnh i trong đồ thị.

Ghi chú

• Với cách biểu diễn ma trận này, ma trận sẽ không thể diễn tả được:
  • Đồ thị có cạnh song song
• Ưu điểm lớn nhất của phương pháp biểu diễn đồ thị bằng ma trận kề là để trả lời câu hỏi: Hai đỉnh u,v có kề nhau trong đồ thị hay không, chúng ta chỉ cần thực hiện một phép so sánh.
• Nhược điểm lớn nhất của phương pháp này là: không phụ thuộc vào số lượng cạnh của đồ thị, ta luôn phải sử dụng n^2 đơn vị bộ nhớ để lưu trữ ma trận kề của nó.

Các đặc điểm

Ma trận kề của một đồ thị vô hướng có tính chất đối xứng, và do đó tồn tại một tập hợp đầy đủ các giá trị riêng (eigenvalue) cùng với cơ sở vectơ riêng (eigenvector) trực giao. Tập hợp các giá trị riêng của đồ thị được gọi là phổ đồ thị.

Giả sử có hai đồ thị, có thể là có hướng hoặc vô hướng, được ký hiệu là G₁ và G₂, với các ma trận kề tương ứng là A₁ và A₂. Hai đồ thị G₁ và G₂ được gọi là đẳng cấu (isomorphic) nếu và chỉ nếu tồn tại một ma trận hoán vị (permutation matrix) P thỏa mãn điều kiện

PA₁P = A_2.

Cụ thể, A₁ và A₂ là các ma trận đồng dạng và do đó chúng có cùng đa thức cực tiểu (minimal polynomial), đa thức đặc trưng (characteristic polynomial), các giá trị riêng, định thức (determinant) và vết ma trận (trace). Vì vậy, chúng có thể được coi là những bất biến đẳng cấu của đồ thị. Khi có hai ma trận kề, có thể tái tạo ma trận hoán vị đã được sử dụng: xem chi tiết tại Ma trận hoán vị.

Tuy nhiên, cần lưu ý rằng điều ngược lại không phải lúc nào cũng đúng: hai đồ thị có thể sở hữu bộ giá trị riêng giống nhau nhưng vẫn không đẳng cấu. Phép nhân với ma trận hoán vị có thể được hiểu như là việc gán nhãn mới cho các cạnh.

Nếu A là ma trận kề của một đồ thị có hướng hoặc vô hướng G, thì ma trận A (được nhân với chính nó n lần) mang một ý nghĩa đặc biệt: ô tại hàng i và cột j cho biết số lượng đường đi (có hướng hoặc vô hướng) có độ dài n từ đỉnh i đến đỉnh j.

Ma trận I − A (trong đó I là ma trận đơn vị kích thước n×n) sẽ khả nghịch khi và chỉ khi đồ thị G không có chu trình có hướng. Khi đó, ma trận nghịch đảo (I − A) cho ta ý nghĩa rằng ô tại hàng i và cột j biểu thị số đường đi có hướng từ đỉnh i tới đỉnh j (giá trị này luôn hữu hạn nếu đồ thị không có chu trình có hướng). Điều này có thể được hiểu thông qua cấp số nhân (geometric series) của các ma trận:

(I − A) = I + A + A + A +...

Điều này tương ứng với việc số đường đi từ i đến j là tổng của số đường đi độ dài 0, cộng với số đường đi độ dài 1, cộng với số đường đi độ dài 2, v.v... Đường chéo chính của mọi ma trận kề tương ứng của đồ thị không có khuyên đều chứa các ô có giá trị bằng 0.

Ma trận kề của đồ thị phân đôi

Một ma trận kề A của một đồ thị phân đôi có r và s đỉnh có cấu trúc như sau:

Trong đó B là ma trận kích thước r × s và O là ma trận toàn số 0. Hiển nhiên, ma trận B là đại diện duy nhất cho đồ thị phân đôi. Ta có G = (U, V, E) là một đồ thị phân đôi với các tập $U=u_1,...,u_r$ và $V=v_1,...,v_s$. Ma trận phân đôi là ma trận B kích thước r × s chỉ chứa các số 0 hoặc 1, trong đó $b_{i,j}=1$ khi và chỉ khi $(u_i,v_j)\in <!--\; \in \; -->E$.

Nếu G là một đa đồ thị phân đôi hoặc đồ thị trọng số phân đôi, thì các phần tử $b_{i,j}$ chứa giá trị tương ứng là bậc của các đỉnh hoặc trọng số của cạnh $(u_i,v_j),$.

Các biến thể

Ma trận kề (0,−1,1) của một đồ thị đơn có a_ii = 0 và a_ij = −1 khi ij là cạnh, còn lại sẽ là 1 nếu không phải. Ma trận này thường được áp dụng trong nghiên cứu đồ thị chính quy mạnh (strongly regular graph) và các đồ thị đôi (two-graph).

Các thỏa hiệp trong vai trò cấu trúc dữ liệu

Khi được sử dụng như một cấu trúc dữ liệu, đối thủ chính của ma trận kề là danh sách kề. Mỗi ô trong ma trận kề chỉ cần một bit, cho phép biểu diễn rất gọn gàng, chỉ tốn n/8 byte bộ nhớ liên tục, với n là số đỉnh. Không chỉ tiết kiệm bộ nhớ, cách lưu trữ này còn thúc đẩy locality of reference (tính địa phương của truy cập bộ nhớ).

Ngược lại, khi áp dụng cho đồ thị thưa, danh sách kề lại tỏ ra ưu việt vì không lưu trữ các cạnh không tồn tại. Sử dụng cài đặt danh sách liên kết đơn giản trên máy tính 32-bit, một danh sách kề cho đồ thị vô hướng cần khoảng 16e byte, với e là số cạnh của đồ thị.

Cần lưu ý rằng một đồ thị có thể có tối đa n cạnh (bao gồm cả các khuyên). Đặt d = e/n là ký hiệu cho mật độ của đồ thị. Ta có: 16e > n/8, nghĩa là danh sách kề sẽ chiếm nhiều không gian hơn khi d > 1/128. Do đó, chỉ nên sử dụng danh sách kề cho đồ thị thưa.

Ngoài việc tiết kiệm bộ nhớ, các cấu trúc dữ liệu khác nhau còn hỗ trợ các thao tác xử lý dữ liệu khác nhau. Với danh sách kề, việc tìm tất cả các đỉnh kề với một đỉnh nhất định trở nên dễ dàng; chỉ cần tra cứu danh sách kề của đỉnh đó. Trong khi với ma trận kề, ta phải quét toàn bộ một hàng, mất thời gian O(n). Nếu muốn kiểm tra xem hai đỉnh cụ thể có nối với nhau hay không, ma trận kề cho phép xác định ngay lập tức, trong khi danh sách kề cần thời gian tỷ lệ thuận với bậc của các đỉnh trong đồ thị.