Mối quan hệ giữa đường thẳng và đường tròn là gì? Toán lớp 9

Bài viết này sẽ giúp bạn hiểu rõ về các mối quan hệ giữa đường thẳng và đường tròn trong chương trình Toán lớp 9. Mời bạn đọc cùng tìm hiểu chi tiết.

1. Các mối quan hệ giữa đường thẳng và đường tròn

1.1. Đường thẳng và đường tròn cắt nhau

- Khi đường thẳng a và đường tròn (O) có hai điểm giao nhau A và B, chúng ta nói rằng đường thẳng và đường tròn (O) cắt nhau.

- Đường thẳng a được gọi là tiếp tuyến của đường tròn (O)

- OH < R

1.2. Khi đường thẳng và đường tròn tiếp xúc nhau

- Nếu đường thẳng a và đường tròn (O) có duy nhất một điểm chung C, thì đường thẳng a và đường tròn (O) được gọi là tiếp xúc nhau

- Đường thẳng a trở thành tiếp tuyến của đường tròn (O) và điểm C là điểm tiếp xúc

- H trùng với C, OC vuông góc với a và OH = R

* Định lý: Một đường thẳng là tiếp tuyến của đường tròn khi nó vuông góc với bán kính đi qua điểm tiếp xúc.

1.3. Đường thẳng và đường tròn không cắt nhau

- Khi đường thẳng a và đường tròn (O) không có điểm chung, chúng ta nói rằng đường thẳng a và đường tròn (O) không cắt nhau

- OH > R

2. Các công thức liên quan đến khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn

  Đường thẳng và đường tròn cắt nhau tại hai điểm Đường thẳng và đường tròn tiếp xúc tại một điểm Đường thẳng và đường tròn không có điểm chungSố điểm giao nhau 2 1 0Quan hệ giữa khoảng cách d và bán kính R d < R d = R d > R

3. Câu hỏi ôn tập về đường thẳng và đường tròn

Câu 1. Cho một đường thẳng a và một điểm O cách đường thẳng 3cm. Vẽ một đường tròn có tâm O và bán kính 5cm.

a. Đường thẳng a có mối quan hệ gì với đường tròn (O)? Giải thích lý do.

b. Gọi B và C là các điểm giao nhau của đường thẳng a và đường tròn (O). Tính khoảng cách giữa B và C.

Câu 2. Cho điểm A nằm trên đường tròn (O; 3m). Tại điểm A, vẽ một tiếp tuyến của đường tròn (O) và chọn điểm B sao cho AB = 4cm. Tính độ dài đoạn OB.

Hướng dẫn giải chi tiết

Vì AB là tiếp tuyến của đường tròn (O; 3cm)

Do đó, AB vuông góc với OA, từ đó suy ra góc BOA = 90 độ

Áp dụng định lý Pythagoras trong tam giác vuông AOB

Câu 3. Cho một đường tròn (O; 15 cm) với dây AB dài 24 cm. Một tiếp tuyến của đường tròn song song với AB cắt đường tròn tại các điểm E và F theo thứ tự. Tính độ dài đoạn EF?

Hướng dẫn giải chi tiết

Rõ ràng rằng tam giác OAB đồng dạng với tam giác OEF, từ đó suy ra tam giác OEF là tam giác cân tại điểm O

Gọi I là điểm tiếp xúc và M là trung điểm của AB

Do OM vuông góc với AB, suy ra OI cũng vuông góc với EF

Xem xét trong tam giác vuông OMB, ta có:

OM = 9 cm

Vì MB song song với IF, áp dụng định lý Thales, ta có:

OM / OI = AB / EF, từ đó EF = 40 cm

Câu 4. Cho tam giác cân ABC (AB = AC) nội tiếp đường tròn (O). Chứng minh rằng: đoạn BC song song với tiếp tuyến tại A của đường tròn (O).

Hướng dẫn giải chi tiết

Gọi d là tiếp tuyến tại điểm A của đường tròn tâm O, vì vậy: d vuông góc với OA (1)

Vì AB = AC, suy ra điểm A nằm trên trung trực của đoạn BC

Ngoài ra, OB = OC, do đó O nằm trên trung trực của đoạn BC

Do đó, OA chính là trung trực của đoạn BC, dẫn đến OA vuông góc với BC (2)

Từ (1) và (2) suy ra rằng, d song song với BC

Câu 5. Cho tam giác ABC vuông tại A (AB < AC), với đường cao AH. E là điểm đối xứng của B qua H. Vẽ đường tròn có đường kính EC cắt AC tại K. Xác định mối quan hệ giữa HK và đường tròn có đường kính EC.

Hướng dẫn giải chi tiết

Gọi I là trung tâm của đường tròn có đường kính EC, I cũng là trung điểm của EC

Vì EC là đường kính của (I) và K nằm trên (I) nên EK vuông góc với KC

Vì K nằm trên AC nên AC vuông góc với EK

Ngoài ra, trong tam giác ABC vuông tại A, ta có AB vuông góc với AC, từ đó suy ra AB // KE

Do đó, tứ giác ABEK là một hình thang (theo định nghĩa hình thang)

Gọi M là trung điểm của AK. Vì E đối xứng với B qua H

Do đó, H là trung điểm của BE, suy ra HM là đường trung bình của hình thang ABEK, nên HM song song với EK, trong khi EK vuông góc với AC, dẫn đến HM vuông góc với AC và cũng vuông góc với AK

HM vừa là đường cao, vừa là đường trung tuyến trong tam giác AHK

=> Tam giác AHK là tam giác cân tại H, do đó góc HAK bằng góc AKH (1)

Vì AK vuông góc với EK và AH vuông góc với BE, nên góc HAK bằng góc KEI và góc EKI

Vì E và K đều nằm trên đường tròn (I) nên IK = IE, dẫn đến tam giác KEI là tam giác cân tại I, do đó góc KEI bằng góc EKI (2)

Từ (1) và (2) ta có: góc AKH = góc EKI, từ đó suy ra góc HKI = góc HKE + góc EKI = góc AKH + góc HKR = góc AKE = 90 độ

Suy ra HK vuông góc với IK, tức là HK là tiếp tuyến của đường tròn có đường kính EC

Câu 6. Trong tam giác ABC vuông tại A (với AB < AC), đường cao AH. E là điểm đối xứng của B qua H. Đường tròn với tâm O và đường kính EC cắt AC tại điểm K. Chứng minh rằng HK là tiếp tuyến của đường tròn (O).

Lời giải chi tiết

Vì trong tam giác EKC, EC là đường kính của đường tròn (O)

EKC bằng 90 độ

Kẻ HI vuông góc với AC, do đó BA song song với HI và EK

Suy ra AI = IK, từ đó tam giác AHK là tam giác cân tại H

Vậy góc K2 bằng góc B (do chúng là các góc phụ của hai góc bằng nhau là góc BAH và góc IHK)

Ngoài ra, góc K2 cũng bằng góc C3 (vì tam giác KOC cân tại O)

góc B cộng góc C3 bằng 90 độ

Do đó, góc K1 cộng góc K2 bằng 90 độ, dẫn đến góc HKO bằng 90 độ

Điều này cho thấy HK là tiếp tuyến của đường tròn (O)

Câu 7. Xét nửa đường tròn (O) với đường kính AB. Qua điểm C nằm trên nửa đường tròn, vẽ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc từ A và B hạ xuống d. Gọi H là chân đường vuông góc từ C hạ xuống AB. Chứng minh:

a. CE bằng CF

b. AC là đường phân giác của góc BAE

c. CH^2 bằng AE nhân BF

Giải chi tiết

a. Chúng ta có: AE vuông góc với d, BF vuông góc với d, vì vậy AE song song với BF

Kết luận, tứ giác AEFB là một hình thang

Hơn nữa, O là trung điểm của AB và OC song song với AE và BF (vì OC vuông góc với d)

Vì vậy, C là trung điểm của EF và do đó CE bằng CF

b. Ta có: AE song song với OC, dẫn đến góc CAE bằng góc ACO (hai góc so le trong) (1)

Ngoài ra, OC bằng OA, do đó tam giác AOC cân tại O, từ đó góc ACO bằng góc OAC (2)

Từ (1) và (2) suy ra góc CAE bằng góc CAO (2)

Kết luận rằng AC là tia phân giác của góc BAE

c. Vì C nằm trên nửa đường tròn với đường kính, nên OC bằng OA bằng OB bằng AB/2

Do đó, tam giác ABC là tam giác vuông tại C

Áp dụng định lý trong tam giác vuông ABC tại C với đường cao CH, ta có:

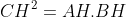
Xem xét tam giác ACE và tam giác ACH vuông, ta có:

Góc AEC bằng góc AHC và đều bằng 90 độ

Góc CAE bằng góc CAH

AC là cạnh chung

Vậy tam giác ACE đồng dạng với tam giác ACH (cạnh huyền - góc nhọn)

Theo phần b, ta có: tam giác ACE đồng dạng với tam giác ACH, nên AH bằng AE (4)

Tương tự, chứng minh và suy ra BH bằng BF (5)

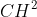
Câu 8. Cho hình vuông ABCD có cạnh bằng a. Gọi M và N lần lượt là hai điểm trên các cạnh AB và AD sao cho chu vi của tam giác AMN bằng 2a. Chứng minh rằng đường thẳng MN luôn tiếp xúc với một đường tròn cố định.

Câu 9. Xét hình thang vuông ABCD với góc A = góc B = 90 độ. O là trung điểm của AB và góc COD bằng 90 độ. Chứng minh rằng CD là tiếp tuyến của đường tròn ngoại tiếp.

Câu 10. Trong tam giác cân ABC tại A với đường cao BH. Trên nửa mặt phẳng chứa C bên bờ AB, vẽ đường vuông góc BX từ B, cắt đường tròn tâm B bán kính BH tại D. Chứng minh rằng CD là tiếp tuyến của đường tròn (B).