Một Câu Hỏi Lớn Về Số Nguyên Tố Nhận Được Một Câu Trả Lời Một Phần

Vào ngày 7 tháng 9, hai nhà toán học đã đăng một bằng chứng của một phiên bản của một trong những vấn đề mở nổi tiếng nhất trong toán học. Kết quả mở ra một mặt trận mới trong nghiên cứu về “định lý số nguyên tố sinh đôi,” làm đau đầu những nhà toán học hơn một thế kỷ và có những ảnh hưởng đối với những đặc điểm sâu sắc nhất của số học.

“Chúng ta đã bế tắc và đang cạn ý tưởng về vấn đề này trong một khoảng thời gian dài, vì vậy khi có ai đó đưa ra những cái nhìn mới là điều tự nhiên hứng thú,” James Maynard, một nhà toán học tại Đại học Oxford, chia sẻ.

Định lý về số nguyên tố sinh đôi liên quan đến các cặp số nguyên tố có hiệu là 2. Ví dụ như 5 và 7 là số nguyên tố sinh đôi. Cũng như 17 và 19. Định lý dự đoán rằng có vô số những cặp như vậy trong dãy số đếm, hoặc số nguyên. Các nhà toán học đã có những tiến bộ đáng kể trong vấn đề này trong thập kỷ qua, tuy nhiên họ vẫn chưa giải quyết được hoàn toàn.

Bằng chứng mới, do Will Sawin của Đại học Columbia và Mark Shusterman của Đại học Wisconsin, Madison, đã giải quyết định lý về số nguyên tố sinh đôi trong một thế giới toán học nhỏ hơn nhưng vẫn quan trọng. Họ chứng minh rằng định lý là đúng trong bối cảnh của các hệ thống số hữu hạn, trong đó bạn chỉ có một số lượng nhỏ các số để làm việc.

Các hệ thống số này được gọi là “các trường số hữu hạn.” Mặc dù kích thước nhỏ, chúng vẫn giữ lại nhiều thuộc tính toán học được tìm thấy trong dãy số nguyên vô tận. Các nhà toán học cố gắng giải các vấn đề số học trên các trường số hữu hạn, sau đó hy vọng dịch kết quả sang dãy số nguyên.

“Ước mơ cuối cùng, một chút ngây thơ có lẽ, là nếu bạn hiểu đủ về thế giới số hữu hạn, điều này có thể làm sáng tỏ thêm về thế giới số nguyên,” James Maynard nói.

Ngoài việc chứng minh định lý về số nguyên tố sinh đôi, Sawin và Shusterman đã tìm ra một kết quả còn mạnh mẽ hơn về hành vi của số nguyên tố trong các hệ thống số nhỏ. Họ chứng minh chính xác cách nào số nguyên tố sinh đôi xuất hiện với tần suất cao trong các khoảng thời gian ngắn — một kết quả thiết lập sự kiểm soát cực kỳ chính xác đối với hiện tượng số nguyên tố sinh đôi. Các nhà toán học mơ về việc đạt được các kết quả tương tự cho các số thông thường; họ sẽ tìm kiếm trong bằng chứng mới để có những hiểu biết có thể áp dụng vào số nguyên tố trên trục số.

Một Loại Số Nguyên Tố Mới

Dự đoán nổi tiếng nhất của định lý về số nguyên tố sinh đôi là có vô số cặp số nguyên tố với hiệu là 2. Nhưng tuyên bố đó rộng lớn hơn. Nó dự đoán rằng có vô số cặp số nguyên tố với hiệu là 4 (ví dụ như 3 và 7) hoặc 14 (293 và 307), hoặc với bất kỳ khoảng cách 2 hoặc lớn hơn mà bạn có thể muốn.

Alphonse de Polignac đặt ra định lý như hiện tại vào năm 1849. Các nhà toán học ít tiến triển trong vấn đề này trong 160 năm tiếp theo. Nhưng vào năm 2013, Yitang Zhang chứng minh rằng có vô số cặp số nguyên tố với khoảng cách không quá 70 triệu. Trong năm tiếp theo, các nhà toán học khác, bao gồm Maynard và Terry Tao, đã giảm khoảng cách số nguyên tố đáng kể. Hiện trạng nghệ thuật hiện nay là một bằng chứng rằng có vô số cặp số nguyên tố với hiệu là tối đa 246.

Nhưng tiến triển về định lý về số nguyên tố sinh đôi đã bị đình trệ. Nhà toán học nhận ra họ sẽ cần một ý tưởng hoàn toàn mới để giải quyết vấn đề hoàn toàn. Hệ thống số hữu hạn là nơi tốt để tìm kiếm một ý tưởng mới.

Để xây dựng một trường số hữu hạn, hãy bắt đầu bằng cách trích xuất một tập hợp số hữu hạn từ các số đếm. Bạn có thể lấy ví dụ như năm số đầu tiên (hoặc bất kỳ giá trị số nguyên tố nào). Thay vì tưởng tượng các số dọc theo một dòng số như chúng ta thường làm, hãy tưởng tượng hệ thống số mới này xung quanh mặt đồng hồ.

Sau đó, phép toán tiếp tục, như bạn có thể hiểu nó, bằng cách quấn quanh mặt đồng hồ. 4 cộng 3 trong hệ thống số hữu hạn với năm phần tử sẽ ra sao? Bắt đầu từ 4, đếm ba ô quanh mặt đồng hồ, bạn sẽ đến 2. Phép trừ, nhân và chia làm việc tương tự.

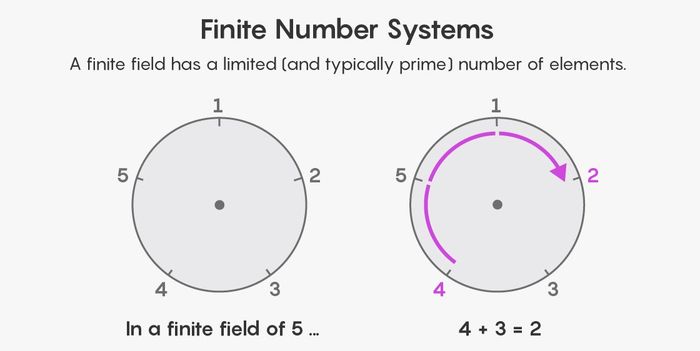
Chỉ có một điều phải lưu ý. Khái niệm thông thường về số nguyên tố không có ý nghĩa đối với các trường số hữu hạn. Trong một trường số hữu hạn, mọi chơi xổ sốu chia hết cho mọi số khác. Ví dụ, 7 thông thường không chia hết cho 3. Nhưng trong một trường số hữu hạn với năm phần tử, nó lại chia hết cho 3. Điều này bởi vì trong trường số hữu hạn này, 7 và 12 đều tương đương với số 2 trên mặt đồng hồ. Do đó, 7 chia cho 3 cũng giống như 12 chia cho 3, và 12 chia cho 3 là 4.

Vì vậy, định lý về số nguyên tố sinh đôi cho các trường số hữu hạn liên quan đến đa thức số nguyên tố — biểu thức toán học như x² + 1.

Ví dụ, giả sử trường số hữu hạn của bạn chứa các số 1, 2 và 3. Một đa thức trong trường số hữu hạn này sẽ có các số đó làm hệ số, và một đa thức “số nguyên tố” sẽ là một đa thức không thể phân tích thành các đa thức nhỏ hơn. Vì vậy x² + x + 2 là số nguyên tố vì nó không thể phân tích, nhưng x² − 1 không phải là số nguyên tố: Đó là tích của (x + 1) và (x − 1).

Khi bạn đã có khái niệm về đa thức số nguyên tố, việc hỏi về đa thức số nguyên tố sinh đôi là hoàn toàn tự nhiên — một cặp đa thức đều là số nguyên tố và chúng khác nhau một khoảng cố định. Ví dụ, đa thức x² + x + 2 là số nguyên tố, cũng như x² + 2x + 2. Hai đa thức này khác nhau bởi đa thức x (cộng x vào đầu tiên để được cái thứ hai).

Định lý về số nguyên tố sinh đôi cho các trường số hữu hạn dự đoán rằng có vô số cặp đa thức số nguyên tố sinh đôi khác nhau không chỉ bởi x, mà bởi bất kỳ khoảng cách nào bạn muốn.

Các Cắt Sạch

Trường số hữu hạn và đa thức số nguyên tố có vẻ như là được bắt chước, ít hữu ích trong việc học về số nói chung. Nhưng chúng giống như một bộ mô phỏng siêu bão — một vũ trụ tự chứa mang lại những hiểu biết về hiện tượng trong thế giới rộng lớn.

“Có một sự tương đồng cổ điển giữa số nguyên và đa thức, cho phép bạn chuyển đổi vấn đề về số nguyên, có thể rất khó khăn, thành vấn đề về đa thức, cũng có thể khó khăn, nhưng có thể dễ giải quyết hơn,” Shusterman nói.

Trường số hữu hạn trở nên nổi bật vào những năm 1940, khi André Weil đề xuất một cách chính xác để chuyển đổi phép toán trong các hệ thống số nhỏ thành phép toán trong số nguyên. Weil sử dụng kết nối này một cách đặc biệt. Ông chứng minh có lẽ là vấn đề quan trọng nhất trong toán học — giả thuyết Riemann — được hiểu theo bối cảnh của các đường cong trên trường số hữu hạn (một vấn đề được biết đến là giả thuyết Riemann hình học). Bằng chứng này, cùng với một loạt các giả thuyết bổ sung mà Weil đưa ra — giả thuyết Weil — đã xác định trường số hữu hạn như một cảnh đẹp phong phú cho khám phá toán học.

Sáng kiến quan trọng của Weil là trong bối cảnh của các trường số hữu hạn, các kỹ thuật từ hình học có thể được sử dụng với sức mạnh thực sự để giải câu hỏi về số. “Điều này là một phần của điều đặc biệt cho các trường số hữu hạn. Nhiều vấn đề bạn muốn giải, bạn có thể diễn đạt lại chúng theo cách hình học,” Shusterman nói.

Để thấy làm thế nào hình học nảy sinh trong một bối cảnh như vậy, hãy tưởng tượng mỗi đa thức như một điểm trong không gian. Các hệ số của đa thức làm nhiệm vụ như các tọa độ xác định vị trí của đa thức. Quay lại trường số hữu hạn của chúng ta với các số 1, 2 và 3, đa thức 2x + 3 sẽ nằm ở điểm (2, 3) trong không gian hai chiều.

Nhưng thậm chí trường số hữu hạn đơn giản nhất cũng có vô số đa thức. Bạn có thể xây dựng đa thức phức tạp hơn bằng cách tăng kích thước của số mũ lớn nhất, hoặc bậc, của biểu thức. Trong trường hợp của chúng ta, đa thức x² − 3x − 1 sẽ được đại diện bởi một điểm trong không gian ba chiều. Đa thức 3x⁷ + 2x⁶ + 2x⁵ − 2x⁴ − 3x³ + x² − 2x + 3 sẽ được đại diện bởi một điểm trong không gian tám chiều.

Trong công việc mới, không gian hình học này đại diện cho tất cả các đa thức của một bậc cố định cho một trường số hữu hạn cụ thể. Câu hỏi đặt ra là: Có cách nào để cô lập tất cả các điểm đại diện cho đa thức số nguyên tố không?

Chiến lược của Sawin và Shusterman là chia không gian thành hai phần. Một phần sẽ chứa tất cả các điểm tương ứng với đa thức có một số lượng yếu tố chẵn. Phần còn lại sẽ chứa tất cả các điểm tương ứng với đa thức có một số lượng yếu tố lẻ.

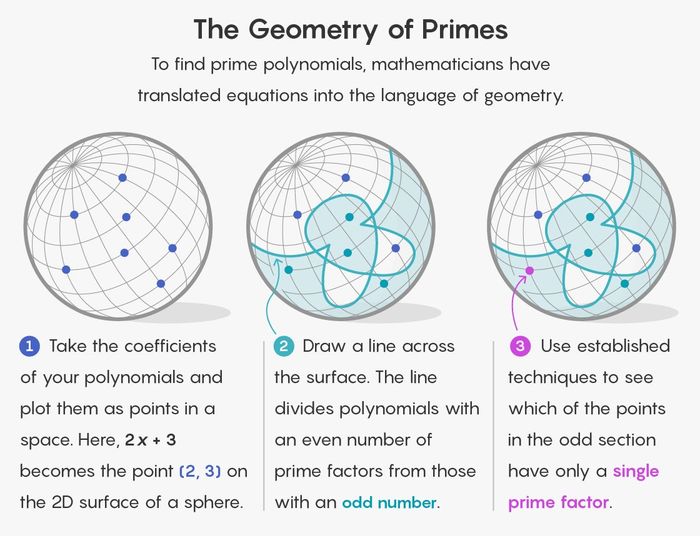
Ngay từ đây, vấn đề đã trở nên đơn giản hơn. Định lý về số nguyên tố sinh đôi cho các trường số hữu hạn liên quan đến đa thức chỉ có một yếu tố (giống như một số nguyên tố chỉ có một yếu tố — chính nó). Và vì 1 là số lẻ, bạn có thể loại bỏ hoàn toàn phần của không gian có yếu tố chẵn.

Mẹo nằm ở việc chia. Trong trường hợp của một đối tượng hai chiều, chẳng hạn như bề mặt của một quả cầu, thứ cắt nó thành hai là một đường cong một chiều, giống như xích đạo cắt bề mặt Trái Đất làm đôi. Một không gian có chiều cao hơn luôn có thể được chia bằng một đối tượng có số chiều ít hơn một.

Tuy nhiên, những hình dạng có số chiều thấp hơn chia không gian của các đa thức không tới mức lịch sự như xích đạo. Chúng được vẽ bằng một công thức toán học gọi là hàm Möbius, nhận một đa thức làm đầu vào và đưa ra 1 nếu đa thức có một số lượng yếu tố nguyên tố chẵn, −1 nếu nó có một số lượng yếu tố nguyên tố lẻ, và 0 nếu nó chỉ có một yếu tố lặp lại (cách 16 có thể được phân thành 2 × 2 × 2 × 2).

Những đường cong được vẽ bởi hàm Möbius xoắn và quay điên cuồng, gặp nhau ở nhiều nơi. Những nơi mà chúng gặp nhau — gọi là điểm đặc biệt — đặc biệt khó phân tích (và chúng tương ứng với đa thức có một yếu tố nguyên tố lặp lại).
Sáng tạo chính của Sawin và Shusterman là tìm ra một cách chính xác để chia những vòng lặp có số chiều thấp hơn thành các đoạn ngắn hơn. Các đoạn này dễ nghiên cứu hơn so với những vòng lặp hoàn chỉnh.

Sau khi liệt kê đa thức có một số lượng yếu tố nguyên tố lẻ — bước khó khăn nhất — Sawin và Shusterman phải xác định đâu là số nguyên tố, và đâu là số nguyên tố sinh đôi. Để làm điều này, họ áp dụng một số công thức mà những nhà toán học sử dụng để nghiên cứu về số nguyên tố trong các số bình thường.

Sawin và Shusterman sử dụng kỹ thuật của họ để chứng minh hai kết quả quan trọng về đa thức số nguyên tố trong một số trường số hữu hạn nhất định.
Đầu tiên, định lý về số nguyên tố sinh đôi cho các trường số hữu hạn là đúng: Có vô số cặp đa thức số nguyên tố sinh đôi, tách biệt bởi bất kỳ khoảng cách nào bạn chọn.

Thứ hai, và quan trọng hơn nhiều, công việc cung cấp một đếm chính xác về số đa thức số nguyên tố sinh đôi mà bạn có thể mong đợi tìm thấy trong số đa thức của một bậc cố định. Nó tương đương với việc biết có bao nhiêu đa thức số nguyên tố sinh đôi trong bất kỳ đoạn đủ dài nào trên dải số — một kết quả mơ ước đối với những nhà toán học.

“Đây là công việc đầu tiên mang lại một phương pháp định lượng cho điều được kỳ vọng là đúng trên các số nguyên, và điều này thực sự nổi bật,” nói Zeev Rudnick của Đại học Tel Aviv. “Cho đến nay, chưa có điều gì giống như thế này.”

Bằng chứng của Sawin và Shusterman cho thấy gần 80 năm sau khi André Weil chứng minh Giả thuyết Riemann trong các đường cong trên trường số hữu hạn, những nhà toán học vẫn đang nỗ lực theo đuổi dấu vết của ông. Những nhà toán học nghiên cứu định lý về số nguyên tố sinh đôi sẽ bây giờ nghía qua công việc của Sawin và Shusterman và hy vọng rằng nó, cũng sẽ cung cấp một nguồn cảm hứng sâu sắc.

Bài viết gốc được tái bản với sự cho phép từ Quanta Magazine, một tờ báo độc lập biên tập thuộc sở hữu của Quỹ Simons, nhiệm vụ của nó là nâng cao sự hiểu biết của công chúng về khoa học bằng cách đưa tin về các phát triển nghiên cứu và xu hướng trong toán học và các ngành khoa học tự nhiên và cuộc sống.

Những bài viết tuyệt vời khác từ MYTOUR

• TikTok—vâng, TikTok—là cửa sổ mới nhất vào chế độ cảnh sát của Trung Quốc
• Một vụ án mạng dã man, một nhân chứng có thể đeo được, và một nghi phạm không tưởng
• Chủ nghĩa tư bản tạo ra tình hình hỗn loạn này, và tình hình hỗn loạn này sẽ làm hủy hoại chủ nghĩa tư bản
• Những con tàu làm sạch có thể làm tăng giá những kỳ nghỉ đắt đỏ hơn
• Sự đối xứng và hỗn loạn của các thành phố siêu lớn trên thế giới
• 👁 Máy móc làm thế nào để học? Ngoài ra, đọc tin tức mới nhất về trí tuệ nhân tạo
• ✨ Tối ưu hóa cuộc sống gia đình của bạn với những lựa chọn tốt nhất của đội ngũ Gear chúng tôi, từ robot hút bụi đến nệm giá rẻ đến loa thông minh.