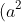Những bài tập Toán nâng cao lớp 9 với đáp án được chọn lọc gần đây

Buzz

Nội dung bài viết

1. Những kiến thức cần lưu ý

2. Loại bài tập toán lớp 9

3. Một số bài tập toán nâng cao lớp 9 có đáp án chọn lọc cho năm học 2023 - 2024

Xem thêm

1. Những kiến thức cần lưu ý

Các điều kiện cơ bản để căn thức có giá trị

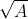
Hàm số y = ax + b (với a khác 0)

- Tính chất: Hàm số đồng biến trên R khi a > 0 và nghịch biến trên R khi a < 0. - Đồ thị: Đồ thị là một đường thẳng đi qua các điểm A(0;b) và B(-b/a;0). 4. Hàm số y = ax² (a ≠ 0)

- Tính chất: Nếu a > 0, hàm số nghịch biến khi x < 0 và đồng biến khi x > 0. Nếu a < 0, hàm số đồng biến khi x < 0 và nghịch biến khi x > 0

- Đồ thị: Đồ thị là một parabol đi qua gốc tọa độ O(0;0). Nếu a > 0, đồ thị nằm trên trục hoành, còn nếu a < 0, đồ thị nằm dưới trục hoành.

Vị trí tương quan của hai đường thẳng

Xem xét hai đường thẳng y = ax + b (d) và y = a'x + b' (d'). Hai đường thẳng (d) và (d') có thể cắt nhau.

⇔ a # a' (d) // (d') ⇔ a = a' ; b # b' (d) trùng (d') ⇔ a = a' và b = b'

Vị trí tương đối giữa đường thẳng và đường cong.

Xem xét đường thẳng y = ax + b (d) và y = ax² (P) (d). Hai đường này giao nhau tại hai điểm (d), tiếp xúc với (P) tại một điểm (d) và (P) không có điểm chung.

Phương trình bậc hai

Xem xét phương trình bậc hai ax² + bx + c = 0 (a # 0)

+ Nếu a + b + c = 0 thì phương trình có hai nghiệm: x1 = 1 và x2 = c/a

+ Nếu a - b + c = 0 thì phương trình có hai nghiệm: x1 = -1 và x2 = -c/a

Giải bài toán bằng cách thiết lập phương trình hoặc hệ phương trình

- Bước 1: Xây dựng phương trình hoặc hệ phương trình

- Bước 2: Giải phương trình hoặc hệ phương trình

- Bước 3: Xác minh các nghiệm của phương trình hoặc hệ phương trình để chọn nghiệm phù hợp với bài toán và đưa ra kết luận

2. Loại bài tập toán lớp 9

Dạng 1: Phân tích theo phương trình ax2 + bx + c = 0 (với a, b, c phụ thuộc vào tham số m).

Xem xét hệ số a: Có hai trường hợp. Nếu a = 0 với một số giá trị của m, giả sử a = 0 ⇔ m = m0, phương trình sẽ trở thành bậc nhất ax + c = 0

+ Nếu b ≠ 0 với m = m0: Phương trình này có một nghiệm x = -c/b

+ Nếu b = 0 và c = 0 với m = m0 thì: () không xác định ⇔ (*) không xác định

+ Nếu b = 0 và c ≠ 0 với m = m0 thì: () không có nghiệm ⇔ (*) không có nghiệm

Dạng 2: Bài toán tính toán

Bài toán 1: Tính giá trị của biểu thức A. Tính A mà không có điều kiện kèm theo tương đương với bài toán

Rút gọn biểu thức A

Bài toán 2: Tính giá trị của biểu thức A(x) với x = a

Cách giải:

- Đơn giản hóa biểu thức A(x).

- Thay x = a vào biểu thức đã đơn giản hóa.

Dạng 3: Chứng minh đẳng thức

Bài toán: Chứng minh rằng A = B

Dạng 3: Các phương pháp chứng minh:

- Phương pháp 1: Dựa vào định nghĩa A = B

⇔ A - B = 0

- Phương pháp 2: Thực hiện các bước biến đổi trực tiếp. A = A1 = A2 = ... = B

- Phương pháp 3: So sánh các giá trị. A = A1 = A2 = ... = C

→ A = B và B = B1 = B2 = ... = C

- Phương pháp 4: Sử dụng quy tắc tương đương. A = B ⇔ A' = B' ⇔ A'' = B''

⇔ ....⇔ () () đã được chứng minh nên A = B

- Phương pháp 5: Áp dụng các giả thiết trong bài toán

- Phương pháp 6: Kỹ thuật quy nạp

- Phương pháp 7: Sử dụng biểu thức phụ

Dạng 4: Chứng minh bất đẳng thức

Bài toán: Chứng minh rằng A lớn hơn B

Dạng 4: Một số bất đẳng thức quan trọng

- Bất đẳng thức Cosi, dấu ' = ' xuất hiện khi và chỉ khi: a1 = a2 = a3 = ... = an Một số phương pháp chứng minh:

- Phương pháp 1: Dựa vào định nghĩa A lớn hơn B ⇔ A - B lớn hơn 0

- Phương pháp 2: Biến đổi trực tiếp A = A1 = A2 = A3 = ... = B + M2 lớn hơn B nếu M không bằng 0

- Phương pháp 3: Sử dụng tương đương A lớn hơn B ⇔ A' lớn hơn B' ⇔ A'' lớn hơn B'' ⇔ .....⇔ (*)

- Phương pháp 4: Áp dụng tính chất bắc cầu A lớn hơn C và C lớn hơn B → A lớn hơn B

- Phương pháp 5: Kỹ thuật phản chứng

Để chứng minh A lớn hơn B, ta giả sử ngược lại là B lớn hơn A và thực hiện các phép biến đổi tương đương cho đến khi dẫn đến mâu thuẫn, từ đó kết luận A lớn hơn B.

- Phương pháp 6: Sử dụng các giả thiết trong bài toán

- Phương pháp 7: Áp dụng quy nạp

- Phương pháp 8: Sử dụng biểu thức phụ để chứng minh

Dạng 5: Giải phương trình bằng cách sử dụng ẩn số phụ

Bài toán 1: Giải phương trình bậc bốn ax4 + bx2 + c = 0

Đặt t = x2 (với t ≥ 0), ta chuyển phương trình thành at2 + bt + c = 0

Giải phương trình bậc hai theo ẩn t, sau đó thay giá trị t vào để tìm ẩn x

Dưới đây là bảng tóm tắt kết quả:

at2 + bt + c = 0	ax4 + bx2 + c = 0
vô nghiệm	vô nghiệm
2 nghiệm âm	vô nghiệm
nghiệm kép âm	vô nghiệm
1 nghiệm dương	2 nghiệm đối nhau
2 nghiệm dương	4 nghiệm 2 cặp nghiệm đối nhau

Bài toán 2: Giải các phương trình bậc cao

Sử dụng các biến đổi để đưa phương trình bậc cao về dạng:

- Phương trình dạng tích

- Phương trình bậc hai

Dạng 6: Giải hệ các phương trình

Giải hệ phương trình: ax + by = c; a'x + b'y = c'

Các phương pháp giải hệ phương trình bao gồm:

- Phương pháp đồ thị

- Phương pháp cộng

- Phương pháp thế

- Phương pháp sử dụng ẩn phụ

Dạng 7: Các bài toán liên quan đến hàm số

Điểm thuộc đường thẳng - đường thẳng đi qua một điểm cụ thể

Bài toán: Cho (C) là đồ thị của hàm số y = f(x) và một điểm A(xA; yA). Hãy xác định xem (C) có đi qua A không?

Đồ thị (C) đi qua A(xA; yA) nếu và chỉ nếu tọa độ của A thỏa mãn phương trình của (C). A thuộc (C) ⇔ yA = f(xA).

Do đó, tính giá trị f(xA)

Nếu f(xA) = yA thì đồ thị (C) đi qua điểm A.

Nếu f(xA) ≠ yA thì đồ thị (C) không đi qua điểm A. Xem xét sự giao nhau của hai đồ thị.

3. Một số bài tập toán nâng cao lớp 9 có đáp án chọn lọc cho năm học 2023 - 2024

Câu hỏi 1: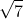 $\sqrt{7}$

Hướng dẫn giải

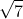
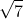
$\sqrt{7}$ $\sqrt{7}$

Đẳng thức này cho thấy m² chia hết cho 7, và vì 7 là số nguyên tố, nên m cũng chia hết cho 7. Đặt m = 7k (với k thuộc Z), ta có m² = 49k² (2).

Từ (1) và (2) ta có 7n² = 49k², suy ra n² = 7k² (3).

Từ (3), n² chia hết cho 7, do đó n cũng chia hết cho 7 vì 7 là số nguyên tố. Vì m và n đều chia hết cho 7, phân số m/n không thể tối giản, điều này mâu thuẫn với giả thiết. Vậy 7 không phải là số hữu tỉ; do đó, 7 là số vô tỉ.

Câu 2: Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x² + y²

Hướng dẫn giải

Cách 1: Với x + y = 2, ta có y = 2 - x. Do đó: S = x² + (2 - x)² = 2(x - 1)² + 2

Vậy giá trị nhỏ nhất của S là 2, xảy ra khi và chỉ khi x = y = 1

Cách 2: Áp dụng bất đẳng thức Bunhiacopxki với a = x, b = y, d = 1, ta có:

(x + y)² ≤ (x² + y²)(1 + 1) ⇒ 4 ≤ 2(x² + y²) = 2S

Do đó, S ≥ 2 ⇒ giá trị nhỏ nhất của S là 2 khi x = y = 1

Câu 3:

a. Cho a, b, c > 0. Chứng minh rằng: bc/a + ca/b + ab/c ≥ a + b + c

b. Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab

Hướng dẫn giải

a. Áp dụng bất đẳng thức Cauchy cho các cặp số dương bc/a và ca/b; bc/a và ab/c; ca/b và ab/c, ta có:

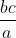
$\frac{bc}{a} + \frac{ca}{b} \geq 2\sqrt{\frac{bc}{a} \cdot \frac{ca}{b}} = 2c; \frac{bc}{a} + \frac{ab}{c} \geq 2\sqrt{\frac{bc}{a} \cdot \frac{ab}{c}} = 2b; \frac{ca}{b} + \frac{ab}{c} \geq 2\sqrt{\frac{ca}{b} \cdot \frac{ab}{c}} = 2a$

Cộng tất cả các vế, ta có bất đẳng thức cần chứng minh. Dấu '=' xuất hiện khi a = b = c

$\frac{3a + 5b}{2} \geq \sqrt{3a \cdot 5b}$

⇒ (3a + 5b)² ≥ 4 cdot 15P (vì P = a cdot b) ⇒ 12² ≥ 60P ⇒ P ≤ 12/5 ⇒ giá trị lớn nhất của P là 12/5

Dấu '=' xảy ra khi 3a = 5b = 12 / 2 ⇒ a = 2; b = 6/5

Câu 4: Cho a³ + b³ = 2. Tìm giá trị lớn nhất của biểu thức N = a + b

Hướng dẫn giải

Đặt a = 1 + x, ta có b³ = 2 – a³ = 2 – (1 + x)³ = 1 – 3x – 3x² – x³ ≤ 1 – 3x + 3x² – x³ = (1 – x)³. Do đó: b ≤ 1 – x.

Vì a = 1 + x, nên: a + b ≤ 1 + x + 1 – x = 2. Với a = 1 và b = 1, ta có a³ + b³ = 2 và a + b = 2.

Vậy giá trị lớn nhất của N là 2 khi a = b = 1

Câu 5: Xác định các giá trị của x sao cho:

a. |2x - 3| = |1 - x| b. x² - 4x ≤ 5 c. 2x(2x - 1) ≤ 2x - 1

Hướng dẫn giải

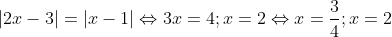
|2x - 3| = |x - 1| ⟺ 2x - 3 = x - 1 hoặc 2x - 3 = -(x - 1). Giải, ta có x = 2 hoặc x = 3/4.

b. x² - 4x ≤ 5 ⟹ (x - 2)² ≤ 9

⟹ |x - 2| ≤ 3, tương đương -3 ≤ x - 2 ≤ 3 ⟹ -1 ≤ x ≤ 5

c. 2x (2x - 1) ≤ 2x - 1 tương đương với (2x - 1)² ≤ 0. Nhưng (2x - 1)² luôn lớn hơn hoặc bằng 0, vì vậy chỉ có thể xảy ra khi 2x - 1 = 0. Do đó, x = 1/2

Câu 6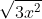

√(3x² + 6x + 7) + √(5x² + 10x + 21) = 5 - 2x - x²

Hướng dẫn giải

Chuyển phương trình về dạng:

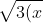
√(3(x+1)² + 4) + √(5(x+1)² + 16) = 6 - (x+1)²

Vế trái của phương trình luôn lớn hơn hoặc bằng 6, trong khi vế phải luôn nhỏ hơn hoặc bằng 6. Do đó, phương trình chỉ đúng khi cả hai vế đều bằng 6, từ đó suy ra x = -1

Câu 7: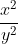

Hướng dẫn giải

Đặt x/y + y/x = a thì x²/y² + y²/x² + 2 = a². Dễ dàng chứng minh rằng x²/y² + y²/x² ≥ 2, nên a² ≥ 4, từ đó |a| ≥ 2 (1). Bất đẳng thức cần chứng minh tương đương với: a² - 2 + 4 ≥ 3a, tức là a² - 3a + 2 ≥ 0, hay (a - 1)(a - 2) ≥ 0 (2)

Từ (1) ta có a ≥ 2 hoặc a ≤ -2. Nếu a ≥ 2, thì (2) là đúng. Nếu a ≤ -2, thì (2) cũng đúng. Bài toán đã được chứng minh.

Câu 8: Cho x, y, z là các số dương. Chứng minh rằng:

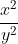
(x²/y²) + (y²/z²) + (z²/x²) ≥ (x/y) + (y/z) + (z/x)

Hướng dẫn giải

$\frac{x^{4}z^{2} + y^{4}x^{2} + z^{4}x^{2} - (x^{2}z + y^{2}x + z^{2}y)xyz}{x^{2}y^{2}z^{2}} \geq 0$

Cần chứng minh tử số không âm, tức là: x³z²(x – y) + y³x²(y – z) + z³y²(z – x) ≥ 0. (1)

Biểu thức không thay đổi khi hoán vị vòng x → y → z → x, do đó có thể giả sử x là số lớn nhất. Xét hai trường hợp:

a) x ≥ y ≥ z > 0. Tách z – x ở (1) thành – (x – y + y – z), (1) tương đương với: x³z²(x – y) + y³x²(y – z) – z³y²(x – y) – z³y²(y – z) ≥ 0 → z²(x – y)(x³ – y²z) + y²(y – z)(yx² – z³) ≥ 0

Dễ dàng thấy x – y ≥ 0, x³ – y²z ≥ 0, y – z ≥ 0, yx² – z³ ≥ 0 nên bất đẳng thức trên là đúng.

b) x ≥ z ≥ y > 0. Tách x – y ở (1) thành x – z + z – y, (1) trở thành: x³z²(x – z) + x³z²(z – y) – y³x²(z – y) – z³y²(x – z) ≥ 0 → z²(x – z)(x³ – zy²) + x²(xz² – y³)(z – y) ≥ 0

Dễ dàng thấy bất đẳng thức trên là đúng.

Một cách khác: Biến đổi bất đẳng thức phải chứng minh tương đương với

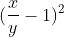$(\frac{x}{y} - 1)^{2} + (\frac{y}{z} - 1)^{2} + (\frac{z}{x} - 1)^{2} + (\frac{x}{y} + \frac{y}{z} + \frac{z}{x}) \geq 3$ Câu 9: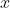 $x + y + z = \sqrt{xy} + \sqrt{yz} + \sqrt{xz}$

Bài giải

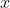
$x + y + z = \sqrt{xy} + \sqrt{yz} + \sqrt{xz} \Rightarrow (\sqrt{x} - \sqrt{y})^{2} + (\sqrt{y} - \sqrt{z})^{2} + (\sqrt{z} - \sqrt{x})^{2} = 0$

Do đó, x = y = z

Câu 10: Chứng minh rằng:

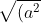
$\sqrt{(a^{2}+c^{2})(b^{2}+c^{2})} + \sqrt{(a^{2}+d^{2})(b^{2}+d^{2})} \geq (a+b)(c+d)$

với a, b, c, d > 0

Giải bài toán

Xem xét tứ giác ABCD với AC vuông góc với BD, và O là điểm giao nhau của hai đường chéo

OA = a; OC = b; OB = c; OD = d với a, b, c, d > 0. Ta có

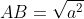
$AB = sqrt{a^{2}+ c^{2}} , BC = sqrt{b^{2}+ c^{2}} , AD= sqrt{a^{2}+ d^{2}} , CD = sqrt{b^{2}+ d^{2}}$

AC = a + b, BD = c + d. Ta cần chứng minh: AB.BC + AD.CD >= AC.BD

Rõ ràng: AB.BC >= 2SABC = AC.BD

Như vậy, ta đã chứng minh điều cần chứng minh.

Lưu ý: Sử dụng bất đẳng thức Bunhiacôpxki với (m2 + n2)(x2 + y2) >= (mx + ny)2 với m = a, n = c, x = c, y = b, ta có

$(a^{2}+c^{2})(c^{2}+b^{2}) geq (ac + bd)^{2} Rightarrow sqrt{(a^{2}+c^{2})(c^{2}+b^{2})}geq ac + cb$

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]