Những công thức cơ bản về phương trình đường thẳng lớp 10 được tổng hợp đầy đủ nhất

Buzz

Nội dung bài viết

1. Vectơ pháp tuyến của đường thẳng

2. Mối quan hệ giữa hai đường thẳng

3. Phương trình chuẩn của đường thẳng

4. Mối liên hệ giữa vectơ chỉ phương và vectơ pháp tuyến

5. Tính khoảng cách từ một điểm đến đường thẳng.

6. Mối quan hệ của hai điểm đối với một đường thẳng.

7. Góc tạo bởi hai đường thẳng.

8. Bài tập áp dụng liên quan

Xem thêm

Bài viết sau đây từ Mytour sẽ cung cấp cho bạn nội dung về 'Những công thức cơ bản về phương trình đường thẳng lớp 10 được tổng hợp đầy đủ nhất'. Hy vọng rằng thông tin trong bài viết sẽ hữu ích cho bạn đọc.

1. Vectơ pháp tuyến của đường thẳng

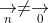
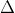
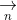
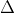
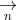
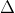
$\underset{n}{\rightarrow} \neq \underset{0}{\rightarrow}$ $\Delta$ $\underset{n}{\rightarrow}$ $\Delta$ $\underset{n}{\rightarrow}$ $\Delta$

+ Trong mặt phẳng tọa độ, mọi đường thẳng đều có thể được biểu diễn bằng phương trình tổng quát như sau:

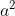
- Đường thẳng có dạng by + c = 0 sẽ song song với hoặc trùng với trục Ox.

- Đường thẳng có dạng ax + c = 0 sẽ song song với hoặc trùng với trục Oy.

- Đường thẳng có dạng ax + by = 0 đi qua gốc tọa độ.

$\frac{x}{a} + \frac{y}{b} = 1 (với a\neq 0 và b\neq 0)$

Phương trình trên được gọi là phương trình đường thẳng dạng đoạn chắn.

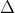
$\Delta$

Nếu b ≠ 0, phương trình này có thể được chuyển đổi thành dạng: y = kx + m (*)

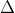
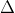
$\Delta$ $\Delta$

2. Mối quan hệ giữa hai đường thẳng

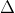
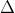
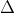
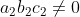
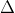
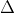
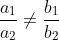
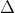
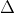
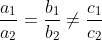
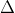
$\Delta$ $\Delta$ $\Delta$ $\Delta$ $\left\{\begin{matrix} a_{1}x + b_{1}y + c_{1} = 0\\ a_{2}x + b_{2}y + c_{2} = 0 \end{matrix}\right.$ $a_{2}b_{2}c_{2} \neq 0$ $\Delta$ $\Delta$ $\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}$ $\Delta$ $\Delta$ $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$ $\Delta$ $\Delta$ $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$

3. Phương trình chuẩn của đường thẳng

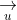
$\Delta$ $\underset{u}{\rightarrow}$ $\frac{x - x_{o}}{a} = \frac{y - y_{o}}{b}$

Phương trình (2) được biết đến là phương trình chuẩn của đường thẳng.

Nếu a = 0 hoặc b = 0, đường thẳng sẽ không có phương trình chuẩn.

4. Mối liên hệ giữa vectơ chỉ phương và vectơ pháp tuyến

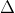
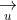
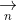
$\Delta$ $\underset{u}{\rightarrow}$ $\underset{n}{\rightarrow}$ $\Delta$

5. Tính khoảng cách từ một điểm đến đường thẳng.

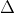
$\Delta$ ax + by + c = 0 được tính bằng công thức:D(M; $\Delta$ $\frac{|ax + by + c|}{\sqrt{a^{2} + b^{2}}}$

6. Mối quan hệ của hai điểm đối với một đường thẳng.

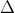
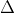
$\Delta$ ax + by + c = 0 $\Delta$ $\Delta$

( axM + byM + c) \cdot (axN + byN + c) > 0.

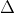
$\Delta$

( axM + byM + c) \cdot (axN + byN + c) < 0.

7. Góc tạo bởi hai đường thẳng.

+ Định nghĩa: Khi hai đường thẳng a và b giao nhau, chúng tạo thành bốn góc. Góc nhỏ nhất trong số đó được gọi là góc giữa hai đường thẳng a và b.

Nếu a song song hoặc trùng với b, chúng ta coi góc giữa chúng là 0 độ.

Ký hiệu: (a; b)

+ Góc giữa hai đường thẳng không vượt quá 90 độ, vì vậy ta có:

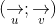
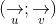
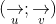
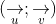
$(\underset{u}{\rightarrow}; \underset{v}{\rightarrow})$ $(\underset{u}{\rightarrow}; \underset{v}{\rightarrow})$ $(\underset{u}{\rightarrow}; \underset{v}{\rightarrow})$ $(\underset{u}{\rightarrow}; \underset{v}{\rightarrow})$

Trong đó, u và v lần lượt là vector pháp tuyến của a và b.

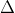
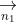
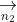
$\Delta$ $\Delta$ $\underset{n_{1}}{\rightarrow}$ $\underset{n_{2}}{\rightarrow}$

$→_{n_{1}}$ $→_{n_{2}}$

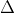
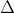
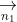
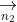
8. Bài tập áp dụng liên quan

Bài 1: Cho đường thẳng d cắt trục Ox tại điểm A(0; 5) và trục Oy tại điểm B(6; 0). Xác định phương trình tổng quát và phương trình đoạn chắn của đường thẳng d.

Giải:

Vì A(0; 5) và B(6; 0) nằm trên đường thẳng d, do đó phương trình đường thẳng có thể xác định dựa vào vectơ chỉ phương của d.

Phương trình đường thẳng và cách giải bài tập chi tiết là (6-0; 0-5) = (6; -5)

Vectơ pháp tuyến của d là (5; 6)

Chọn điểm A(0; 5) nằm trên đường thẳng d, ta có phương trình tổng quát của d là:

5.(x – 0) + 6.(y – 5) = 0

Phương trình đường thẳng là 5x + 6y – 30 = 0

$\frac{x}{6} + \frac{y}{5} = 1$

Bài 2: Cho đường thẳng d đi qua hai điểm M(5; 8) và N(3; 1). Xác định phương trình tham số và phương trình chính tắc của đường thẳng d.

Giải:

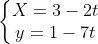
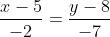
$→_{MN}$ $→_{MN}$ $\left\{\begin{matrix} x = 3 - 2t\\ y = 1 - 7t \end{matrix}\right.$ $\frac{x-5}{-2} = \frac{y-8}{-7}$

Bài 3: Xem xét mối quan hệ giữa các cặp đường thẳng sau:

a) d1: 4x - 10y + 1 = 0 và d2: x + y + 2 = 0.

b) d3: 12x - 6y + 10 = 0 và d4: 2x - y + 5 = 0.

c) d5: 8x + 10y - 12 = 0 và d6: 4x + 5y - 6 = 0.

Giải:

a) Xem xét hai đường thẳng d1: 4x - 10y + 1 = 0 và d2: x + y + 2 = 0. Vì hệ số x của d1 và d2 khác nhau (4 và 1), do đó d1 và d2 cắt nhau.

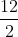
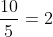
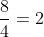$\frac{12}{2}$ $\frac{10}{5} = 2$ $\frac{8}{4} = 2$ Bài 4: $\left\{\begin{matrix} x = 4 - 3t\\ y = 7 + 2t \end{matrix}\right.$

Giải chi tiết:

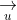
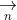
$\left\{\begin{matrix} x = 4 - 3t\\ y = 7 + 2t \end{matrix}\right.$ $\underset{u}{\rightarrow}$ $\underset{n}{\rightarrow}$

Chọn điểm M (4; 7) nằm trên đường thẳng d, ta có phương trình tổng quát của d là:

2.(x – 4) + 3.(y – 7) = 0

Phương trình đường thẳng là 2x – 8 + 3y – 21 = 0

Phương trình đường thẳng là 2x + 3y – 29 = 0

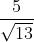$\frac{5}{\sqrt{13}}$ Bài 5:

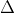: 5x + 12y - 10 = 0.

Giải chi tiết:

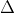: 5x + 12y - 10 = 0.

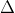Chúng ta có:R = d(C,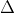

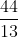
$\frac{44}{13}$

Bài 6: Xét tam giác ABC với các phương trình đường thẳng: (AB): 2x - 3y - 1 = 0, (BC): x + 3y + 7 = 0, và (AC): 5x - 2y + 1 = 0. Tìm phương trình của đường thẳng BH.

A. 6x + 5y + 37 = 0

B. 6x - 5y + 37 = 0

C. 6x + 5y - 37 = 0

D. 2x + 5y + 37 = 0

Đáp án: A. Phương trình của đường thẳng BH là: 6x + 5y + 37 = 0

Bài 7: Hình vuông ABCD có điểm A(−1; 2). Đường chéo (BD) có phương trình x + y − 1 = 0. Tìm phương trình của 4 cạnh của hình vuông.

A. x + 1 = 0; y = 0; x − 3 = 0; y − 2 = 0

B. x + 1 = 0; y = 0; x + 3 = 0; y + 2 = 0

C. x + 1 = 0; y = 0; x + 3 = 0; y − 2 = 0

D. x - 1 = 0; y = 0; x - 3 = 0; y - 2 = 0

Đáp án: C. x + 1 = 0; y = 0; x + 3 = 0; y − 2 = 0

Bài 8: Cho hai điểm A(1; 1) và B(2; 3). Tìm phương trình của đường thẳng (d) sao cho khoảng cách từ A đến (d) là 2 và khoảng cách từ B đến (d) là 4.

A. y + 1 = 0 và 4x − 3y + 3 = 0.

B. y + 1 = 0 và 4x + 3y − 3 = 0.

C. y + 1 = 0 và 2x + 3y + 3 = 0.

D. y + 1 = 0 và 4x + 3y + 3 = 0.

Đáp án: D. y + 1 = 0 và 4x + 3y + 3 = 0.

Đây là bài viết của Mytour, hy vọng nó đã cung cấp kiến thức hữu ích để bạn có thể nắm vững lý thuyết và giải quyết các bài tập liên quan. Mytour xin chân thành cảm ơn bạn đã dành thời gian đọc bài viết này!

Nội dung từ Mytour nhằm chăm sóc khách hàng và khuyến khích du lịch, chúng tôi không chịu trách nhiệm và không áp dụng cho mục đích khác.

Nếu bài viết sai sót hoặc không phù hợp, vui lòng liên hệ qua email: [email protected]