Phạm vi của hàm số

Một phần của loạt bài về
Vi tích phân
Định lý cơ bản Quy tắc tích phân Leibniz Giới hạn của hàm số Tính liên tục Định lý giá trị trung bình Định lý Rolle
Vi phân[hiện] Định nghĩa Đạo hàm (Tổng quát) Vi phân vô cùng bé hàm số toàn phần Khái niệm Ký hiệu vi phân Đạo hàm bậc hai Vi phân ẩn Định lý Taylor Quy tắc và đẳng thức Cộng Nhân Dây chuyền Lũy thừa Chia Quy tắc l'Hôpital Hàm ngược Leibniz tổng quát Công thức Faà di Bruno
Tích phân[hiện] Danh sách tích phân Biến đổi tích phân Định nghĩa Nguyên hàm Tích phân (suy rộng) Tích phân Riemann Tích phân Lebesgue Tích phân theo chu tuyến Tích phân của hàm ngược Kỹ thuật Từng phần Đĩa Vỏ Thế (lượng giác, Weierstrass, Euler) Công thức Euler Đổi trật tự Công thức truy hồi Lấy đạo hàm dưới dấu tích phân
Chuỗi[hiện] Hình học (số học-hình học) Điều hòa Đan dấu Lũy thừa Nhị thức Taylor Tiêu chuẩn hội tụ Số hạng d'Alembert Cauchy Tích phân So sánh So sánh giới hạn Chuỗi đan dấu Cô đọng Cauchy Dirichlet Abel
Vectơ[hiện] Gradien Div Rot Laplace Đạo hàm có hướng Đẳng thức Định lý Gauss Gradient Green Kelvin–Stokes Stokes
Nhiều biến[hiện] Chủ đề Ma trận Tenxơ Đạo hàm ngoài Hình học Định nghĩa Đạo hàm riêng Tích phân bội Tích phân đường Tích phân mặt Tích phân thể tích Ma trận Jacobi Ma trận Hesse
Chuyên ngành[hiện] Malliavin Ngẫu nhiên Phép tính biến phân
Thuật ngữ[hiện] Thuật ngữ giải tích

Trong toán học, phạm vi của hàm số (Tiếng Anh: functional limit) là một khái niệm cơ bản trong vi tích phân và giải tích liên quan đến hành vi của hàm số đó gần một giá trị nhất định.

Định nghĩa chính thức, bắt nguồn từ đầu thế kỷ thứ 19, được trình bày ở dưới. Phi chính thức, một hàm số f gán một giá trị đầu ra f(x) cho mỗi giá trị đầu vào x. Ta nói hàm số có giới hạn L tại giá trị a: nghĩa là f(x) tiến càng ngày càng gần L khi x tiến càng gần a. Cụ thể hơn, với bất kỳ giá trị đầu vào nào đủ gần với a, kết quả nhận được phải gần tùy ý đến L. Ngược lại, ta nói giới hạn không tồn tại.

Khái niệm về phạm vi có nhiều ứng dụng trong giải tích hiện đại. Cụ thể, nhiều định nghĩa của tính liên tục sử dụng giới hạn: một hàm số gọi là liên tục nếu tất cả giới hạn của nó bằng với giá trị của nó. Giới hạn cũng xuất hiện trong định nghĩa của đạo hàm: trong giải tích một biến, đạo hàm là giá trị giới hàm của độ dốc của đường cát tuyến với đồ thị của một hàm số.

Lịch sử

Trong quá trình phát triển giải tích vào thế kỷ 17 và 18, khái niệm về giới hạn của hàm số bắt nguồn từ Bolzano, người đã giới thiệu kỹ thuật epsilon-delta để định nghĩa hàm số liên tục vào năm 1817. Công trình của ông không được biết đến cho đến khi ông qua đời (Felscher 2000). Trong quyển sách Cours d'analyse năm 1821, Cauchy thảo luận về biến số, giới hạn và tính liên tục của hàm số y = f(x) bằng cách mô tả rằng một biến đổi rất nhỏ trong x dẫn đến một biến đổi rất nhỏ trong y, đồng thời (Grabiner 1983) cho rằng ông chỉ có thể giải thích bằng từ ngữ. Weierstrass là người đầu tiên sử dụng định nghĩa epsilon-delta cho giới hạn, một định nghĩa vẫn được sử dụng rộng rãi ngày nay. Ông cũng sử dụng các ký hiệu như $lim$ và $\underset{x\to <!--\; \to \; -->x_0}{lim}$ (Burton 1997).

Ký hiệu hiện đại

Giả sử có một người đang đi trên đồ thị của hàm số y = f(x). Hoành độ của người đó là giá trị của biến x, còn tung độ là giá trị của y. Người đó đi lại gần với vị trí có hoành độ là a. Khi người đó tiến đến gần vị trí đó, cô ta nhận ra rằng độ cao của cô tiếp xúc là L. Nếu được hỏi về độ cao tại điểm x = a, cô ấy sẽ trả lời là L.

Ký hiệu mũi tên dưới ký hiệu giới hạn xuất phát từ Hardy trong cuốn sách A Course of Pure Mathematics xuất bản năm 1908 (Miller 2004).

Vậy, nói đến việc cô ấy tiến đến gần L, có nghĩa là độ cao của cô ấy sẽ gần với L với sai số có thể làm nhỏ xuống. Ví dụ, nếu chúng ta đặt sai số bé hơn mười mét, cô ấy nói rằng cô ấy có thể làm được điều đó bằng cách tiến gần hơn đến vị trí a, ví dụ như trong khoảng cách năm mươi mét (theo chiều ngang). Tức là, miễn là cô ấy đứng không quá năm mươi mét từ a, độ cao của cô sẽ cách L không quá mười mét.

Tương tự, không cần phải là mười mét, nếu yêu cầu sai số giảm xuống một mét, cô ấy vẫn có thể đạt được độ cao mong muốn bằng cách tiến gần hơn đến a. Tóm lại, nói rằng cô ấy tiến gần đến vị trí a là nói rằng với mọi sai số tối đa, dù nhỏ tới đâu, vẫn tồn tại một khu vực xung quanh a mà trong đó độ cao của cô ấy nằm trong sai số yêu cầu đó.

Lời giải thích trên có thể được sử dụng như sau:

Giới hạn của hàm số f(x) khi x tiến tới p là một số L thỏa mãn tính chất: với bất kỳ khoảng cách nào từ L, tồn tại một vùng xung quanh p sao cho giá trị của f(x) nằm trong khoảng đã cho.

Phát biểu trên gần với định nghĩa hoàn chỉnh của giới hạn của một hàm số trong không gian Hausdorff. Định nghĩa này, thường được gọi là định nghĩa (ε, δ), được chấp nhận rộng rãi trong nhiều hoàn cảnh khác nhau.

Một hàm số một biến

Cho hàm f: R → R được định nghĩa trên tập số thực và a, L ∈ R. Nếu khi x tiến tới a, ta nói giới hạn của f là L và viết

$\underset{x\to <!--\; \to \; -->a}{lim}f\left(x\right)=L,$

Với mọi số thực ε > 0, tồn tại một số thực δ > 0 sao cho với mọi x thỏa mãn 0 < |x − a| < δ thì |f(x) − L| < ε.

Có thể thấy giới hạn của hàm số không phụ thuộc vào cách hàm số f được định nghĩa tại a, và cũng không phụ thuộc vào giá trị của hàm số f tại a, tức f(a).

Các ký hiệu ε và δ có thể hiểu là 'sai số' và 'khoảng cách', và thực tế là Cauchy đã sử dụng ε để viết tắt cho 'sai số' trong một số tác phẩm của ông (Grabiner 1983), mặc dù trong định nghĩa về tính liên tục, ông sử dụng α rất nhỏ thay vì ε hoặc δ (xem Cours d'Analyse).

Giới hạn một phía

Thay vì tiếp cận từ cả hai phía, x có thể tiến tới a từ bên phải hoặc bên trái, khi đó giới hạn được gọi là giới hạn bên phải (bên trái) của f tại a, ký hiệu là

$\underset{x\to <!--\; \to \; -->a^{+}}{lim}f\left(x\right)=L$

cho giới hạn từ phía phải, và

$\underset{x\to <!--\; \to \; -->a^{-<!--\; -\; -->}}{lim}f\left(x\right)=L$

cho giới hạn từ phía trái. Nếu cả hai giới hạn này tồn tại và bằng nhau, thì giới hạn của f tại a cũng tồn tại và bằng giá trị của hai giới hạn từ một phía. Nếu các giới hạn này tồn tại nhưng không bằng nhau thì giới hạn của f tại a không tồn tại. Nếu một trong hai giới hạn từ một phía này không tồn tại thì giới hạn tại a cũng không tồn tại.

Một định nghĩa chi tiết như sau:

• Giới hạn của f(x) khi x tiến tới a từ phía phải (hay từ phía trên) là L nếu, với mọi ε > 0, tồn tại một số δ > 0 sao cho nếu 0 < x − a < δ thì |f(x) − L| < ε.
• Giới hạn của f(x) khi x tiến tới a từ phía trái (hay từ phía dưới) là L nếu, với mọi ε > 0, tồn tại một số δ > 0 sao cho nếu 0 < a − x < δ thì |f(x) − L| < ε.

Lưu ý rằng nếu cả hai điều kiện 0 < x − a < δ và 0 < a − x < δ đều đúng thì tương đương với 0 < |x − a| < δ

Ví dụ minh họa

Giới hạn một phía không tồn tại

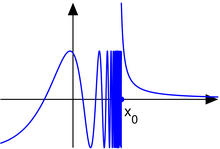
Hàm số

không có giới hạn tại x₀ = 1: giới hạn từ bên trái không tồn tại do tính dao động của hàm sin, giới hạn từ bên phải không tồn tại do hàm nghịch đảo tiệm cận về vô cùng. Tuy nhiên, hàm số này có giới hạn tại mọi điểm khác ngoài 1 trên trục số thực.

Hàm Dirichlet, được định nghĩa là f(x) = 1 nếu x là số hữu tỉ và f(x) = 0 nếu x là số vô tỉ, không có giới hạn tại bất kì điểm nào trong tập số thực.

Giới hạn từ một phía không bằng nhau

Hàm số

có giới hạn tại mọi điểm x khác 0 (giới hạn là 1 với x âm và 2 với x dương). Giới hạn tại x = 0 không tồn tại, do giới hạn từ bên trái (là 1) và giới hạn từ bên phải (là 2) là khác nhau.

Giới hạn tại một điểm

Hàm số f: R → R, được định nghĩa là f(x) = x nếu x là số hữu tỉ và f(x) = 0 nếu x là số vô tỉ, có giới hạn tại x = 0 và giới hạn đó bằng 0.

Giới hạn tại vô số điểm đếm được

Hàm số f, được định nghĩa f(x) = sin x với x vô tỉ và f(x) = 1 với x hữu tỉ, có giới hạn tại mọi điểm có dạng π/2 + 2nπ, trong đó n là một số nguyên bất kỳ.

Hàm số trên không gian mêtric

Giả sử M và N lần lượt là tập con của không gian metric A và B, và ánh xạ f: M → N, với x ∈ M và a là một điểm giới hạn của M và L ∈ N. Ta nói giới hạn của f khi x tiến tới a là L và viết

$\underset{x\to <!--\; \to \; -->a}{lim}f\left(x\right)=L$

nếu tính chất sau thỏa: với mọi

ε > 0, tồn tại một δ > 0 sao cho nếu 0 < d_A(x, a) < δ thì d_B(f(x), L) < ε.

Cũng như trên, để ý rằng a không nhất thiết nằm trong tập xác định của f, cũng như L không nhất thiết nằm trong tập giá trị của f, và ngay cả khi f(a) có nghĩa, nó cũng không nhất thiết bằng L.

Một định nghĩa khác sử dụng khái niệm lân cận. Ta viết

$\underset{x\to <!--\; \to \; -->p}{lim}f\left(x\right)=L$

nếu với mọi lân cận V của L trong B, tồn tại một lân cận U của a trong A sao cho f(U ∩ M − {a}) ⊆ V.

Hàm số trên không gian tôpô

Giả sử X, Y là các không gian tôpô với Y là một không gian Hausdorff. Gọi p là một điểm giới hạn của Ω ⊆ X, và L ∈ Y. Với hàm số f: Ω → Y, ta nói giới hạn của f khi x tiến tới p là L (tức là, f(x) → L khi x → p) và viết:

$\underset{x\to <!--\; \to \; -->p}{lim}f\left(x\right)=L$

nếu điều kiện sau đây được thỏa mãn: với mọi lân cận mở V của L, tồn tại một lân cận mở U của p sao cho f(U ∩ Ω − {p}) ⊆ V.

Để ý rằng tập xác định của f không nhất thiết phải chứa p, và nếu có thì giá trị của f tại p không ảnh hưởng đến định nghĩa của giới hạn. Cụ thể, nếu tập xác định của f là X {p} (hoặc toàn bộ X), thì giới hạn của f khi x → p tồn tại và bằng L nếu, với mọi tập con Ω của X có điểm giới hạn p, giới hạn của f trên Ω tồn tại và bằng L. Đôi khi điều kiện này được dùng để thiết lập sự không tồn tại của giới hạn hai bên của một hàm số trên R bằng cách chỉ ra các giới hạn một bên không tồn tại hoặc không bằng nhau.

Ngoài ra, điều kiện Y là một không gian Hausdorff có thể được nói lỏng thành một không gian tôpô nói chung, nhưng khi ấy giới hạn của hàm số có thể không còn là duy nhất. Cụ thể, ta nói một giới hạn hoặc tập các giới hạn của hàm số tại mộ điểm.

Một hàm số liên tục tại điểm giới hạn p nằm trong tập xác định của nó khi và chỉ khi f(p) là (một) giới hạn của f(x) khi x tiến tới p.

Giới hạn có vô cùng

Giới hạn tại vô cùng

Với hàm số thực f(x), ta nói giới hạn của f khi x tiến tới (dương) vô cùng là L, viết là

$\underset{x\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}f\left(x\right)=L,$

nghĩa là với mọi ε > 0, tồn tại một số c sao cho nếu x > c thì |f(x) - L| < ε. Viết bằng ký hiệu là:

.

Tương tự, ta nói giới hạn của f khi x tiến tới âm vô cùng là L, viết là

$\underset{x\to <!--\; \to \; -->-<!--\; -\; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}f\left(x\right)=L,$

nghĩa là với mọi ε > 0, tồn tại một số c sao cho nếu x < c thì |f(x) - L| < ε. Viết bằng ký hiệu là:

.

Ví dụ: $\underset{x\to <!--\; \to \; -->-<!--\; -\; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}{e}^x=0.$

Giới hạn vô cùng

Với hàm số có giá trị tăng đến vô cùng, nó phân kỳ và giới hạn thông thường không tồn tại. Tuy nhiên, trong trường hợp này ta có thể định nghĩa giới hạn với giá trị vô cùng. Ví dụ, phát biểu giới han của f khi x tiến tới a là vô hạn, viết là

$\underset{x\to <!--\; \to \; -->a}{lim}f\left(x\right)=\mathrm{\infty <!--\; \infty \; -->},$

nghĩa là với mọi N > 0, tồn tại một số δ > 0 sao cho nếu 0 < |x - a| < δ thì f(x) > N.

Những định nghĩa này có thể được kết hợp với nhau một cách tự nhiên để cho ta những loại giới hạn tương tự như

$\underset{x\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}f\left(x\right)=\mathrm{\infty <!--\; \infty \; -->},\underset{x\to <!--\; \to \; -->a^{+}}{lim}f\left(x\right)=-<!--\; -\; -->\mathrm{\infty <!--\; \infty \; -->}.$

Ví dụ,

$\underset{x\to <!--\; \to \; -->0^{+}}{lim}\ln <!--\; \; -->x=-<!--\; -\; -->\mathrm{\infty <!--\; \infty \; -->}.$

Những giới hạn vô hạn có liên quan đến khái niệm tiệm cận.

Những định nghĩa trên có cách tiếp cận sử dụng không gian mêtric. Thực tế, chúng tương thích với định nghĩa không gian tôpô của giới hạn nếu

• một lân cận của −∞ được định nghĩa để chứa một đoạn [−∞, c) với c ∈ R, và
• một lân cận của ∞ được định nghĩa để chứa một đoạn (c; ∞) với c ∈ R, và
• một lân cận của a ∈ R được định nghĩa như trong không gian mêtric R.

Trong trường hợp đó, R là một không gian tôpô và định nghĩa không gian tôpô cho giới hạn áp dụng cho bất kì hàm số f: X → Y với X, Y ⊆ R, khi ấy giới hạn vô cùng có thể được định nghĩa dễ dàng.

Giới hạn tại vô hạn của hàm phân thức

Có ba quy tắc cơ bản để tính giới hạn tại dương vô cùng của một hàm phân thức f(x) = P(x)/Q(x) (trong đó P và Q là các đa thức):

• Nếu bậc của P lớn hơn bậc của Q, thì giới hạn là dương hoặc âm vô cùng, tùy thuộc vào dấu của hệ số bậc cao nhất của hai đa thức (cùng dấu là dương, ngược dấu là âm);
• Nếu bậc của P và Q bằng nhau, giới hạn bằng hệ số bậc cao nhất của P chia cho hệ số bậc cao nhất của Q;
• Nếu bậc của P nhỏ hơn bậc của Q, giới hạn là 0.

Nếu giới hạn (hữu hạn) tại vô cùng của f tồn tại, nó tượng trưng cho tiệm cận ngang tại y = L. Đa thức không có tiệm cận ngang, tuy nhiên các hàm phân thức có thể có.

Hàm số nhiều biến

Để ý rằng |x − a| tượng trưng cho khoảng cách trên trục số, định nghĩa của giới hạn có thể được mở rộng cho hàm số của nhiều hơn một biến. Trong trường hợp hai biến, với hàm số f: R → R, ta viết

$\underset{(x,y)\to <!--\; \to \; -->(a,b)}{lim}f(x,y)=L$

nếu

với mọi ε > 0, tồn tại một δ > 0 sao cho với mọi (x,y) thỏa mãn 0 < ||(x,y) − (a,b)|| < δ, thì |f(x,y) − L| < ε

trong đó ||(x,y) − (a,b)|| là khoảng cách Euclid. Định nghĩa này có thể được mở rộng cho số biến bất kỳ.

Hoàn cảnh khác

Dãy số

Với hàm số trên trục số thực, một cách để định nghĩa giới hạn của một hàm số là bằng giới hạn của dãy số. (định nghĩa này thường được cho là của Eduard Heine). Trong hoàn cảnh này:

$\underset{x\to <!--\; \to \; -->a}{lim}f\left(x\right)=L$

nếu và chỉ nếu với mọi dãy số x_n (x_n khác a với mọi n) hội tụ về a, dãy f(x_n) hội tụ về L. Năm 1916, Sierpiński chứng minh sự tương đương của định nghĩa này và định nghĩa ở trên, sử dụng một dạng yếu hơn của tiên đề chọn. Chú ý rằng để định nghĩa một dãy x_n hội tụ về a vẫn cần định nghĩa (ε, δ) của giới hạn.

Tương tự với định nghĩa của Weierstrass, một định nghĩa Heine tổng quát hơn áp dụng cho hàm số định nghĩa trên tập con của tập số thực. Gọi f là một hàm số giá trị thực với tập xác định D, a là giới hạn của một dãy các phần tử thuộc D {a}. Khi ấy giới hạn của f là L khi x tiến tới a nếu

với mọi dãy x_n ∈ D {a} mà hội tụ về a thì dãy f(x_n) hội tụ về L.

Giải tích không chính quy

Trong giải tích không chính quy, giới hạn của hàm số được định nghĩa là:

$\underset{x\to <!--\; \to \; -->a}{lim}f\left(x\right)=L$

khi và chỉ khi với mọi x ∈ R, nếu x - a vô cùng nhỏ thì f(x) - L là vô cùng nhỏ.

Ở đây R là tập số siêu thực và f là mở rộng tự nhiên của f cho tập số thực không chính quy. Keisler chứng minh rằng định nghĩa giới hạn sử dụng số siêu thực giúp đơn giản hóa đi hai biến. Mặt khác, Karel Hrbacek viết rằng để những định nghĩa như thế hợp lệ cho mọi số siêu thực, chúng vẫn phải gián tiếp sử dụng phương pháp ε-δ, và cho rằng, từ góc nhìn sư phạm, việc giải tích không chính quy có thể được thực hiện mà không cần phương pháp ε-δ là khó khả thi. Piotr Błaszczyk và những người khác chỉ ra sự hữu dụng của liên tục vi mô trong việc xây dựng một định nghĩa rõ ràng cho tính liên tục đều, và đánh giá chỉ trích của Hrbacek là 'lời than vãn mơ hồ'.

Độ gần

Tại hội nghị toán học quốc tế 1908, nhà toán học Frigyes Riesz giới thiệu một cách khác để định nghĩa giới hạn và tính liên tục sử dụng một khái niệm gọi là 'độ gần'. Một điểm x được gọi là 'gần' một tập S ⊆ R nếu với mọi r > 0, tồn tại một a ∈ S sao cho |x - a| < r. Trong trường hợp này, ta có

$\underset{x\to <!--\; \to \; -->a}{lim}f\left(x\right)=L$

khi và chỉ khi với mọi tập A ⊆ R, nếu a gần A thì L gần f(A). Ở đây f(A) ký hiệu cho tập {f(x) | x ∈ A}. Định nghĩa này cũng có thể mở rộng cho không gian mêtric và không gian tôpô.

Tính liên tục

Khái niệm giới hạn của hàm số liên quan chặt chẽ đến khái niệm tính liên tục. Một hàm số f được gọi là liên tục tại c nếu nó có nghĩa tại c và giá trị của nó tại c bằng giới hạn của f khi x tiến tới c:

$\underset{x\to <!--\; \to \; -->c}{lim}f\left(x\right)=f\left(c\right).$

(Ở đây ta giả sử c là một điểm giới hạn trong miền xác định của f.)

Tính chất

Phép tính đại số

Cho hàm số f: M → N giữa hai không gian mêtric M và N. Nếu N là một không gian định chuẩn thì toán tử giới hạn là tuyến tính theo nghĩa sau:

• Nếu giới hạn của f(x) và g(x) khi x tiến tới a lần lượt là L và K thì giới hạn của f(x) + g(x) khi x tiến tới a là L + K
• Nếu α là một scalar từ trường của N thì giới hạn của αf(x) khi x tiến tới a là αL.

Nếu f là một hàm số thực (hoặc phức) thì việc lấy giới hạn vẫn bảo toàn các phép toán đại số thông thường, với điều kiện rằng các giới hạn bên phải tồn tại (phương trình cuối chỉ đúng khi mẫu số bên trái khác không).

Trong từng trường hợp nêu trên, ngay cả khi giới hạn ở vế phải không tồn tại hoặc giới hạn của tử và mẫu trong đẳng thức cuối cùng đều bằng không (gọi là dạng bất định), thì giới hạn ở vế trái vẫn có thể tồn tại, tuỳ thuộc vào các hàm số f và g. Ví dụ, nếu f(x) = 1/x và g(x) = −1/x, khi đó:

Một ví dụ khác là hàm sinc f(x) = sin x/x, đã được giới thiệu ở trên. Cả sin x và x đều tiến về 0 khi x tiến về 0, tuy nhiên f(x) có giới hạn là 1 khi x tiến về 0.

Những quy tắc trên cũng áp dụng được với giới hạn một bên, giới hạn vô cùng và giới hạn âm vô cùng, theo những quy tắc sau:

• q + ∞ = ∞ với q ≠ −∞
• q × ∞ = ∞ với q > 0
• q × ∞ = −∞ với q < 0
• q / ∞ = 0 với q ≠ ± ∞

(xem trục số thực mở rộng)

Lưu ý rằng không có quy tắc tổng quát nào cho trường hợp q/0; tất cả phụ thuộc vào các hàm số đã cho. Các dạng bất định—ví dụ như 0/0, 0×∞, ∞−∞, và ∞/∞—cũng không thể áp dụng những quy tắc trên được, nhưng thường có thể được tính bằng quy tắc l'Hôpital hoặc định lý kẹp.

Giới hạn của hàm hợp

Nói chung, khi có

$\underset{y\to <!--\; \to \; -->b}{lim}f\left(y\right)=c$ và $\underset{x\to <!--\; \to \; -->a}{lim}g\left(x\right)=b$,

ta không suy ra được $\underset{x\to <!--\; \to \; -->a}{lim}f\left(g\right(x\left)\right)=c$. Tuy nhiên, quy tắc này là đúng nếu một trong hai điều kiện sau được thỏa mãn:

• f(b) = c (tức là f liên tục tại b), hoặc
• g không nhận giá trị b ở gần a (tức là, tồn tai một δ > 0 sao cho nếu 0 < |x - a| < δ thì g(x) ≠ b

Một ví dụ cụ thể, ta xét hai hàm không thỏa mãn cả hai điều kiện trên:

Dễ thấy rằng

$\underset{x\to <!--\; \to \; -->a}{lim}f\left(x\right)=0$ với mọi $a$.

Do đó, áp dụng quy tắc hợp mà không dùng điều kiện trên dẫn đến giới hạn của f(f(x)) là 0. Tuy nhiên, thực tế là

và do đó

$\underset{x\to <!--\; \to \; -->a}{lim}f\left(f\right(x\left)\right)=1$ với mọi $a$.

Giới hạn đặc biệt

Hàm phân thức

Với số nguyên không âm n và các hằng số a₁, a₂, a₃,..., a_n và b₁, b₂, b₃,..., b_n

• $\underset{x\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}\frac{a_1{x}^n+a_2{x}^{n-<!--\; -\; -->1}+a_3{x}^{n-<!--\; -\; -->2}+...+a_n}{b_1{x}^n+b_2{x}^{n-<!--\; -\; -->1}+b_3{x}^{n-<!--\; -\; -->2}+...+b_n}=\frac{a_1}{b_1}$

Điều này có thể chứng minh bằng cách chia cả tử và mẫu cho x. Nếu đa thức ở tử có bậc lớn hơn đa thức ở mẫu, giới hạn này không tồn tại (bằng vô cùng). Nếu đa thức ở tử có bậc nhỏ hơn thì giới hạn này bằng 0.

Hàm lượng giác

Giới hạn của sin(x)/x khi x tiến gần đến 0 là 1

Hàm mũ

Giới hạn của (1 + x)^(1/x) khi x tiến gần đến 0 là e

Giới hạn của (e^x - 1)/x khi x tiến gần đến 0 là 1

• $\underset{x\to <!--\; \to \; -->0}{lim}\frac{\ln <!--\; \; -->(1+x)}{x}=1$

$\underset{x\to <!--\; \to \; -->0}{lim}\frac{\ln <!--\; \; -->(1+ax)}{bx}=\frac{a}{b}$

$\underset{x\to <!--\; \to \; -->0}{lim}\frac{{\log }_c<!--\; \; -->(1+ax)}{bx}=\frac{a}{b\ln <!--\; \; -->c}$

Quy tắc l'Hôpital

Quy tắc này sử dụng đạo hàm để tìm giới hạn của dạng bất định như 0/0 hay ±∞/∞, và chỉ áp dụng được trong những trường hợp đó. Cho hai hàm số f(x) và g(x), được định nghĩa trên một khoảng mở I chứa điểm giới hạn c. Nếu cả bốn điều kiện sau đều được thỏa mãn:

$\underset{x\to <!--\; \to \; -->c}{lim}\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to <!--\; \to \; -->c}{lim}\frac{f^{\prime }\left(x\right)}{g^{\prime }\left(x\right)}$

Ví dụ: $\underset{x\to <!--\; \to \; -->0}{lim}\frac{\sin <!--\; \; -->\left(2x\right)}{\sin <!--\; \; -->\left(3x\right)}=\underset{x\to <!--\; \to \; -->0}{lim}\frac{2\cos <!--\; \; -->\left(2x\right)}{3\cos <!--\; \; -->\left(3x\right)}=\frac{2\cdot <!--\; \cdot \; -->1}{3\cdot <!--\; \cdot \; -->1}=\frac{2}{3}.$

Tổng và tích phân

Thay vì viết giới hạn ở vô cùng, ta thường đặt vô cùng lên các chặn của tổng hoặc tích phân.Ví dụ:

$\underset{n\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}\underset{i=s}{\overset{n}{\sum <!--\; \sum \; -->}}f\left(i\right)=\underset{i=s}{\overset{\mathrm{\infty <!--\; \infty \; -->}}{\sum <!--\; \sum \; -->}}f\left(i\right)$

$\underset{x\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}{\int <!--\; \int \; -->}_a^{x}f\left(t\right)dt=\underset{f}{{\int <!--\; \int \; -->}_a^{\mathrm{\infty <!--\; \infty \; -->}}}$