Phân Phối Chuẩn: Định Nghĩa, Công Dụng, và Công Thức

Định Nghĩa về Phân Phối Chuẩn

Phân phối chuẩn, còn được gọi là phân phối Gaussian, là một phân phối xác suất có đối xứng quanh giá trị trung bình, cho thấy rằng dữ liệu gần giá trị trung bình xảy ra thường xuyên hơn so với dữ liệu xa giá trị trung bình. Phân phối chuẩn xuất hiện dưới dạng 'đường cong chuông' khi được biểu diễn đồ thị.

Những Điều Quan Trọng Cần Biết

Các Đặc Điểm của Phân Phối Chuẩn

Phân phối chuẩn là loại phân phối phổ biến nhất được giả định trong phân tích kỹ thuật thị trường chứng khoán. Phân phối chuẩn tiêu chuẩn có hai tham số: trung bình và độ lệch chuẩn. Trong phân phối chuẩn, giá trị trung bình (trung bình), trung vị (điểm giữa), và mode (quan sát phổ biến nhất) bằng nhau. Những giá trị này đại diện cho đỉnh cao nhất hoặc điểm cao nhất. Sau đó, phân phối rơi vào đối xứng quanh giá trị trung bình, chiều rộng của nó được xác định bởi độ lệch chuẩn.

Mô hình phân phối chuẩn là chìa khóa của Định lý Giới hạn Trung tâm (CLT) mà nó khẳng định rằng các trung bình tính từ các biến ngẫu nhiên độc lập, cùng phân phối có phân phối gần như chuẩn, bất kể loại phân phối mà các biến này được lấy mẫu từ.

Phân phối chuẩn là một loại phân phối đối xứng. Các phân phối đối xứng xảy ra khi một đường chia tách tạo ra hai hình ảnh đối xứng. Không phải tất cả các phân phối đối xứng đều là phân phối chuẩn vì một số dữ liệu có thể xuất hiện như hai đỉnh hay một chuỗi đồi núi ngoài đường cong chuông chỉ ra phân phối chuẩn.

Quan sát

Quy tắc kinh nghiệm

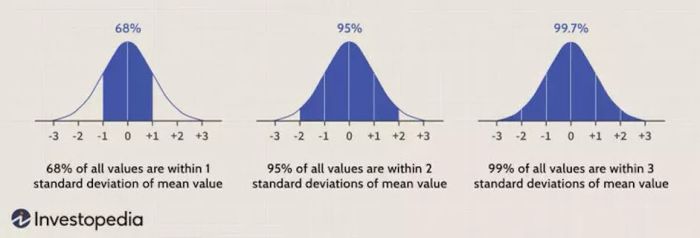
Đối với tất cả các phân phối chuẩn, 68.2% quan sát sẽ xuất hiện trong khoảng cách +/- một độ lệch chuẩn so với giá trị trung bình; 95.4% sẽ nằm trong khoảng +/- hai độ lệch chuẩn; và 99.7% nằm trong khoảng +/- ba độ lệch chuẩn.

Sự thật này đôi khi được gọi là 'quy tắc kinh nghiệm,' một hướng dẫn đơn giản mô tả nơi mà hầu hết dữ liệu trong phân phối chuẩn sẽ xuất hiện. Dữ liệu rơi vào bên ngoài ba độ lệch chuẩn ('3-sigma') sẽ chỉ ra các sự kiện hiếm hoi.

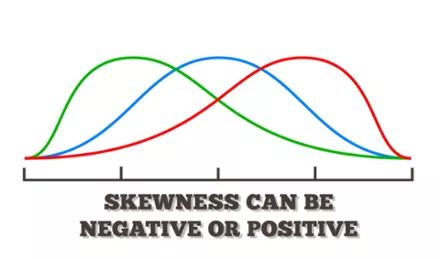
Độ Xiên

Độ xiên đo độ đối xứng của một phân phối. Phân phối chuẩn là đối xứng và có độ xiên bằng không. Nếu phân phối của một tập dữ liệu có độ xiên nhỏ hơn không, hoặc độ xiên âm (độ xiên bên trái), thì đuôi bên trái của phân phối dài hơn đuôi bên phải; độ xiên dương (độ xiên bên phải) ngụ ý rằng đuôi bên phải của phân phối dài hơn đuôi bên trái.

Độ nhọn đỉnh

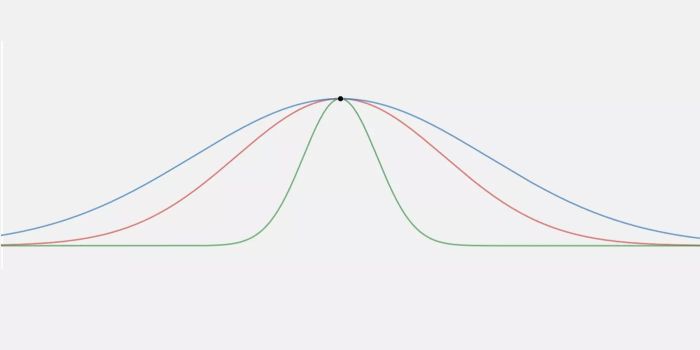
Độ nhọn đỉnh đo độ dày của hai đuôi của phân phối so với đuôi của phân phối. Phân phối chuẩn có độ nhọn đỉnh bằng 3.0. Các phân phối có độ nhọn đỉnh lớn hơn 3.0 thể hiện dữ liệu đuôi vượt quá đuôi của phân phối chuẩn (ví dụ, năm hoặc nhiều hơn độ lệch chuẩn từ giá trị trung bình).

Sự dư thừa nhọn đỉnh này được biết đến trong thống kê là leptokurtic, nhưng được gọi một cách thông tục là 'đuôi mập.' Sự xuất hiện của đuôi mập trên thị trường tài chính mô tả điều được gọi là rủi ro đuôi. Các phân phối có độ nhọn đỉnh thấp hơn 3.0 (platykurtic) thường có đuôi ít cực đoan hơn ('mỏng') so với đuôi của phân phối chuẩn.

Công thức

Phân phối chuẩn tuân theo công thức sau đây. Lưu ý rằng chỉ các giá trị của trung bình (μ) và độ lệch chuẩn (σ) là cần thiết

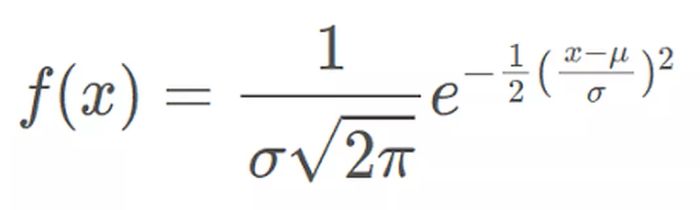
nơi:

• x = giá trị của biến số hoặc dữ liệu đang được xem xét và f(x) là hàm xác suất
• μ = giá trị trung bình
• σ = độ lệch chuẩn

Cách Phân phối Chuẩn được Sử dụng trong Tài chính

Giả thuyết về phân phối chuẩn được áp dụng vào giá tài sản và hành động giá. Các nhà giao dịch có thể vẽ các điểm giá để phù hợp với hành động giá gần đây vào một phân phối chuẩn. Điều này cho thấy, càng xa hành động giá đi khỏi giá trung bình, càng có khả năng cao là tài sản đang bị định giá quá cao hoặc quá thấp. Các nhà giao dịch có thể sử dụng độ lệch chuẩn để đề xuất các giao dịch tiềm năng. Loại giao dịch này thường được thực hiện trên khung thời gian rất ngắn vì các khung thời gian lớn làm cho việc chọn điểm vào và điểm ra trở nên khó khăn hơn nhiều.

Tương tự, nhiều lý thuyết thống kê cố gắng mô hình giá tài sản và giả định rằng chúng tuân theo một phân phối chuẩn. Trên thực tế, phân phối giá thường có đuôi dày và do đó có độ nhọn đỉnh lớn hơn ba. Những tài sản này đã có các biến động giá lớn hơn ba độ lệch chuẩn so với giá trị trung bình thường xuyên hơn là dự đoán theo giả thuyết của phân phối chuẩn. Ngay cả khi một tài sản đã trải qua một giai đoạn dài phù hợp với phân phối chuẩn, không có đảm bảo rằng hiệu suất quá khứ thực sự cho biết về tương lai.

Ví dụ về Phân phối Chuẩn

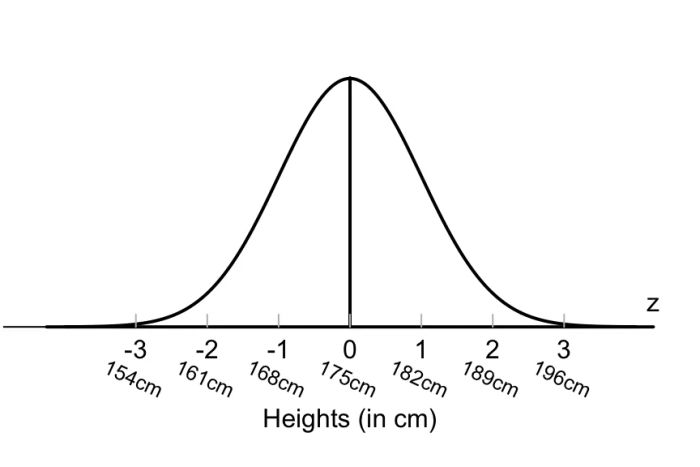
Nhiều hiện tượng tự nhiên có vẻ được phân phối theo phân phối chuẩn. Ví dụ, chiều cao trung bình của con người khoảng 175 cm (5' 9'), tính cả nam và nữ.

Như biểu đồ dưới đây cho thấy, hầu hết mọi người tuân theo chiều cao trung bình đó. Người cao và ngắn tồn tại với tần suất giảm dần trong dân số. Theo quy tắc kinh nghiệm, 99,7% mọi người sẽ rơi vào khoảng +/- ba độ lệch chuẩn so với giá trị trung bình, tức là từ 154 cm (5' 0') đến 196 cm (6' 5'). Những người cao hơn và thấp hơn điều này sẽ hiếm (chỉ 0,15% dân số mỗi bên).

Ý nghĩa của Phân phối Chuẩn là gì?

Tại sao Phân phối Chuẩn được gọi là 'Chuẩn'?

Giới hạn của Phân phối Chuẩn trong Tài chính là gì?

Tóm lại

Phân phối chuẩn, cũng được biết đến là phân phối Gaussian, là một phân phối xác suất mà xuất hiện như một 'đường cong chuông' khi được biểu đồ hóa. Phân phối chuẩn mô tả một biểu đồ đối xứng của dữ liệu xung quanh giá trị trung bình của nó, trong đó độ rộng của đường cong được xác định bởi độ lệch chuẩn.