Toán học đằng sau tài chính có thể hơi rắc rối và nhàm chán. May mắn thay, hầu hết các chương trình máy tính thực hiện các phép tính phức tạp. Tuy nhiên, hiểu các thuật ngữ và phương pháp thống kê khác nhau, ý nghĩa của chúng, và xác định phương pháp phân tích đầu tư nào tốt nhất là rất quan trọng khi lựa chọn các chứng khoán phù hợp và đạt được tác động mong muốn đối với danh mục đầu tư.
Một quyết định quan trọng khác là lựa chọn giữa phân phối normal và phân phối lognormal, hai phân phối này thường được nhắc đến trong văn liệu nghiên cứu. Trước khi lựa chọn, bạn cần biết:
- Nó là gì
- Sự khác biệt giữa chúng là gì
- Làm thế nào chúng ảnh hưởng đến các quyết định đầu tư
Phân phối Normal và Phân phối Lognormal
Cả phân phối chuẩn và phân phối logarit chuẩn được sử dụng trong toán học thống kê để mô tả xác suất của một sự kiện xảy ra. Lật đồng xu là một ví dụ dễ hiểu về xác suất. Nếu bạn lật đồng xu 1000 lần, phân phối kết quả sẽ như thế nào? Tức là, nó sẽ rơi vào mặt ngửa hoặc mặt sấp bao nhiêu lần? Có 50% xác suất nó sẽ rơi vào mặt ngửa hoặc mặt sấp. Ví dụ cơ bản này mô tả xác suất và phân phối kết quả.
Có nhiều loại phân phối, trong đó có phân phối chuẩn hay còn gọi là phân phối chuông.
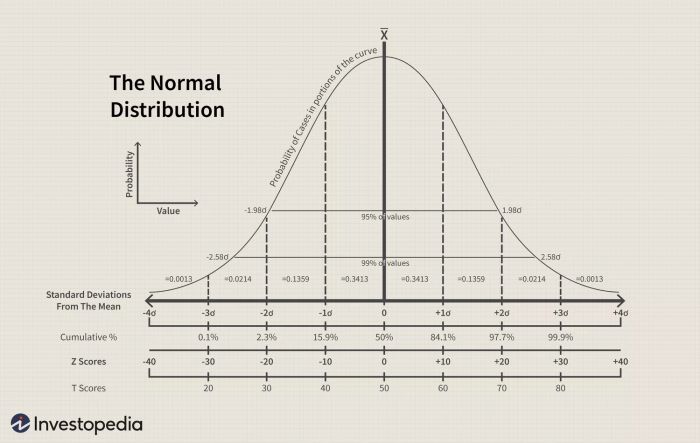
Trong phân phối chuẩn, 68% (34%+34%) kết quả nằm trong một độ lệch chuẩn, và 95% (68%+13.5%+13.5%) nằm trong hai độ lệch chuẩn. Tại trung tâm (điểm 0 trong hình ảnh trên), trung vị (giá trị ở giữa tập hợp), mốt (giá trị xảy ra nhiều nhất) và trung bình (trung bình cộng) là như nhau.
Phân phối logarit-nhân khác với phân phối chuẩn trong một số cách. Một khác biệt chính là trong hình dạng của nó: phân phối chuẩn là đối xứng, trong khi phân phối logarit-nhân thì không. Bởi vì các giá trị trong phân phối logarit-nhân là dương, chúng tạo ra một đường cong lệch phải.
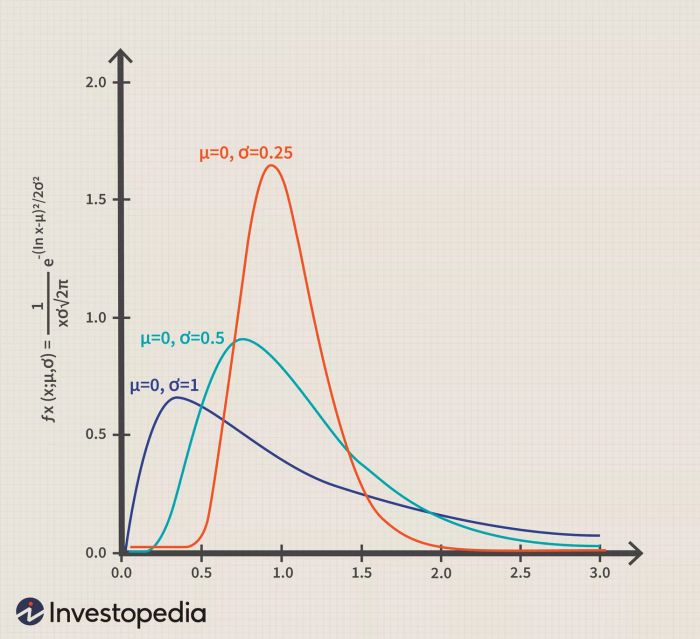
Sự lệch của phân phối này là quan trọng trong việc xác định phân phối nào thích hợp để sử dụng trong quyết định đầu tư. Một sự khác biệt khác là các giá trị được sử dụng để suy ra phân phối logarit-nhân thường là phân phối chuẩn.
Hãy làm rõ bằng một ví dụ. Một nhà đầu tư muốn biết giá cổ phiếu tương lai dự kiến. Vì các cổ phiếu tăng trưởng theo tỷ lệ lũy tiến, họ cần sử dụng một yếu tố tăng trưởng.
Để tính các mức giá dự kiến có thể, họ sẽ lấy giá cổ phiếu hiện tại và nhân với các tỷ lệ lợi nhuận khác nhau (các yếu tố mũ được tính toán toán học dựa trên sự tích lũy), được cho là phân phối bình thường. Khi nhà đầu tư liên tục tích lũy lợi nhuận, họ tạo ra một phân phối logarit chuẩn.
Phân phối này luôn là dương ngay cả khi một số tỷ lệ lợi nhuận là âm, điều này sẽ xảy ra 50% thời gian trong phân phối bình thường. Giá cổ phiếu tương lai luôn là dương vì giá cổ phiếu không thể giảm xuống dưới 0 đô la.
Khi nào thì sử dụng phân phối Chuẩn so với Logarit Chuẩn
Ví dụ trước đã giúp chúng ta đến điều thực sự quan trọng đối với các nhà đầu tư: khi nào để sử dụng mỗi phương pháp. Phân phối Logarit Chuẩn rất hữu ích khi phân tích giá cổ phiếu. Miễn là yếu tố tăng trưởng được sử dụng được cho là phân phối bình thường (như chúng ta giả định với tỷ lệ lợi nhuận), thì phân phối logarit chuẩn có ý nghĩa. Phân phối Chuẩn không thể được sử dụng để mô hình hóa giá cổ phiếu vì nó có mặt âm, và giá cổ phiếu không thể giảm xuống dưới mức 0.
Một ứng dụng tương tự khác của phân phối logarit chuẩn là trong việc định giá các lựa chọn. Mô hình Black-Scholes—được sử dụng để định giá các lựa chọn—sử dụng phân phối logarit chuẩn làm cơ sở để xác định giá các lựa chọn.
Ngược lại, phân phối chuẩn hoạt động tốt hơn khi tính toán tổng lợi nhuận của danh mục. Phân phối chuẩn được sử dụng vì lợi nhuận trung bình có trọng số (tích của trọng số của một chứng khoán trong danh mục và tỷ lệ lợi nhuận của nó) mô tả chính xác hơn tổng lợi nhuận thực tế của danh mục (dương hoặc âm), đặc biệt là nếu các trọng số dao động nhiều.
| Portfolio Holdings | Weights | Returns | Weighted Returns |
| Stock A | 40% | 12% | 40% * 12% = 4.8% |
| Stock B | 60% | 6% | 60% * 6% = 3.6% |
| Total Weighted Average Return | 4.8% + 3.6% = 8.4% |
Mặc dù lợi nhuận logarit chuẩn cho hiệu suất tổng thể của danh mục có thể nhanh hơn khi tính toán trong một khoảng thời gian dài, nó không thể nắm bắt được trọng số của từng cổ phiếu, điều này có thể làm sai lệch lợi nhuận một cách nghiêm trọng. Ngoài ra, tổng lợi nhuận của danh mục có thể là dương hoặc âm, và phân phối logarit chuẩn sẽ không thể nắm bắt được các khía cạnh tiêu cực.
Kết Luận Cuối Cùng
Mặc dù những sắc thái phân biệt giữa các phân phối chuẩn và logarit chuẩn có thể là khó nhận biết đối với chúng ta hầu hết thời gian, hiểu biết về hình dạng và đặc điểm của mỗi phân phối sẽ cung cấp cái nhìn sâu sắc về cách mô hình hóa tổng lợi nhuận danh mục và giá cổ phiếu trong tương lai.
