
Trong toán học, đặc biệt là trong phân tích hàm, tích chập là phép toán thực hiện với hai hàm số f và g, tạo ra một hàm số mới. Phép tích chập khác biệt với tương quan chéo vì nó yêu cầu lật kernel theo cả hai chiều trước khi tính tổng tích. Nó được áp dụng trong nhiều lĩnh vực như xác suất, thống kê, thị giác máy tính, xử lý ảnh, xử lý tín hiệu, kỹ thuật điện, học máy và các phương trình vi phân.
Khái niệm
Tích chập của hai hàm số ƒ và g được ký hiệu là ƒ∗g, là một dạng đặc biệt của phép biến đổi tích phân:
Trong trường hợp tổng quát, nếu f và g là các hàm số phức trong không gian R, thì tích chập của chúng được định nghĩa như sau:
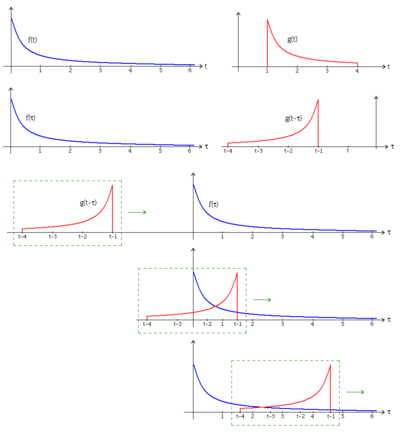
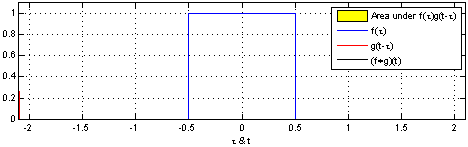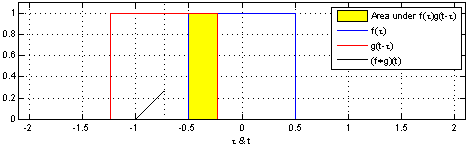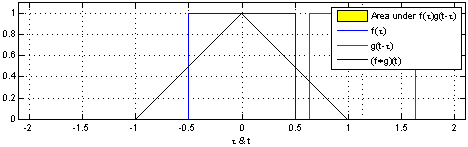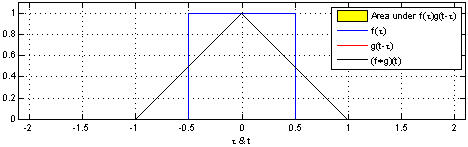
| Hình ảnh minh họa tích chập. | |
|---|---|
|
|
Tích chập theo chu kỳ
Nếu hàm số gT có chu kỳ , và hàm f sao cho ƒ∗gT tồn tại, thì tích chập của chúng cũng có chu kỳ T và được định nghĩa như sau:
Với to là một giá trị bất kỳ.
Tích chập rời rạc
Đối với các hàm số phức f và g được xác định trên tập số nguyên Z, tích chập của chúng được định nghĩa như sau:
Các tính chất
Thuộc về đại số
Tích chập là một phép toán trên không gian của các hàm tuyến tính khả tích, do đó nó có các tính chất giao hoán, kết hợp và phân phối.
- Giao hoán
- Kết hợp
- Quy tắc phân phối
- Phép nhân vô hướng kết hợp
- , trong đó là một số phức bất kỳ.
- Bracewell, R. (1986), Chuyển đổi Fourier và Ứng dụng của nó (ấn bản 2), McGraw–Hill, ISBN 0071160434.
- Hewitt, Edwin; Ross, Kenneth A. (1979), Phân tích hàm trừu tượng. Tập I, Grundlehren der Mathematischen Wissenschaften [Nguyên lý cơ bản của Khoa học Toán học], 115 (ấn bản 2), Berlin, New York: Springer-Verlag, ISBN 978-3-540-09434-0, MR 0551496.
- Hewitt, Edwin; Ross, Kenneth A. (1970), Phân tích hàm trừu tượng. Tập II: Cấu trúc và phân tích cho các nhóm compact. Phân tích trên các nhóm Abelian địa phương compact, Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlin, New York: Springer-Verlag, MR 0262773.
- Hörmander, L. (1983), Phân tích các toán tử đạo hàm riêng tuyến tính I, Grundl. Math. Wissenschaft., 256, Springer, ISBN 3-540-12104-8, MR 0717035.
- Kassel, Christian (1995), Các nhóm lượng tử, Graduate Texts in Mathematics, 155, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94370-1, MR 1321145.
Liên kết tham khảo
- Những ứng dụng đầu tiên: Mục về Convolution có thông tin lịch sử.
- Convolution Lưu trữ 2006-02-21 tại Wayback Machine, trên The Data Analysis BriefBook Lưu trữ 2006-05-12 tại Wayback Machine
- http://www.jhu.edu/~signals/convolve/index.html Ứng dụng Java Applet cho phép biến đổi hình ảnh trực quan.
- http://www.jhu.edu/~signals/discreteconv2/index.html Ứng dụng Java Applet cho phép biến đổi hình ảnh theo thời gian rời rạc.
- Bài giảng về Xử lý Hình ảnh: Một bộ sưu tập 18 bài giảng định dạng pdf từ Đại học Vanderbilt. Bài giảng 7 là về biến đổi 2-D, bởi Alan Peters.
- http://www.vuse.vanderbilt.edu/~rap2/EECE253/EECE253_01_Intro.pdf Lưu trữ 2009-03-24 tại Wayback Machine
- Hướng dẫn tương tác về Hoạt động Đầu vào Kernel Convolution
- Convolution tại MathWorld
- Freeverb3 Impulse Response Processor: Bộ xử lý phản hồi xung mã nguồn mở với các plugin VST
- Stanford University CS 178 trình diễn Flash tương tác cho thấy cách hoạt động của biến đổi không gian.
