
Ở hai phần trước, bạn đọc đã được giới thiệu ví dụ và phương pháp giải của hai chủ đề chính trong phần thi Toán (Math Section) của bài thi chuẩn hoá SAT. Trong phần cuối này, bạn đọc sẽ được cung cấp thông tin và phương pháp giải cho các dạng bài trong hai chủ đề chính còn lại trong SAT Math Section là Nền tảng toán học cao cấp (Passport to Advanced Maths) và Các chủ đề khác (Miscellaneous).
Những kiến thức cơ bản về toán học cao cấp trong SAT Math
Các phép toán với đa thức
Yêu cầu cần thiết
Dạng bài này yêu cầu thí sinh sử dụng thành thạo các phép toán cộng, trừ, nhân, chia đa thức và viết lại biểu thức.
Ví dụ minh họa
Cùng xem xét câu hỏi dưới đây:
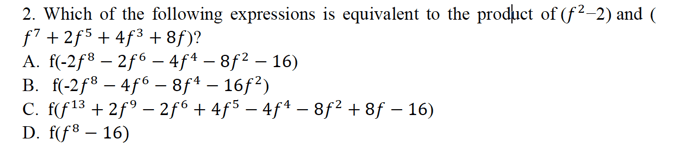
Kiến thức quan trọng
Với dạng bài này, thí sinh cần nắm chắc kiến thức về tính toán, khai triển đa thức, bao gồm: Phân tích đa thức thành nhân tử, tính chất phân phối, tính chất kết hợp trong đa thức (Những kiến thức nằm trong chương trình Toán học lớp 8 tại Việt Nam).
Biểu thức tổng quát:
(a+b)(c+d)=a(c+d)+b(c+d)=ac+ad+bc+bd
Chiến lược đạt được mục tiêu
Đa phần các bài tính toán trong SAT sẽ mang tính chất mẹo nhiều hơn là tính toán một cách máy móc. Vậy nên thí sinh nên rèn luyện thói quen nhận xét các đáp án để tìm câu trả lời nhanh nếu có thể, lựa chọn sau cùng mới dùng đến tính toán. Điều này sẽ giúp thí sinh mất ít thời gian hơn với những câu hỏi không quá phức tạp và có nhiều thời gian hơn cho những câu thực sự thử thách trong bài thi.
Phân tích và giải thích ví dụ
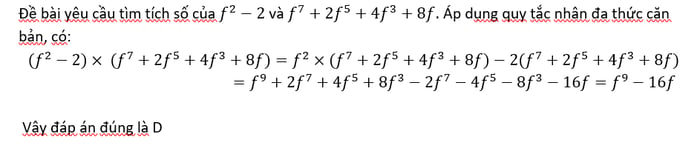
Cách làm nhanh: Nếu để ý kỹ một chút, thí sinh có thể nhận thấy số hạng có số mũ lớn nhất mà phép nhân có thể tạo ra là , mà hệ số của là 1. Do đó phương án A, B loại vì có hệ số của là -2, phương án C loại vì xuất hiện số hạng .
Hàm số và phương trình bậc hai
Loại bài 1: Giải phương trình bậc hai
Yêu cầu
Dạng bài này yêu cầu thí sinh giải phương trình bậc 2. Ngoài ra một số dạng bài nâng cao hơn có thể được phát triển từ dạng bài này, ví dụ như phương trình trùng phương (bậc chẵn, có dạng tương đương với phương trình bậc 2), phương trình đa thức bậc cao (phân tích được thành phương trình bậc 1 và 2).
Ví dụ minh họa
Cùng xem xét câu hỏi dưới đây:
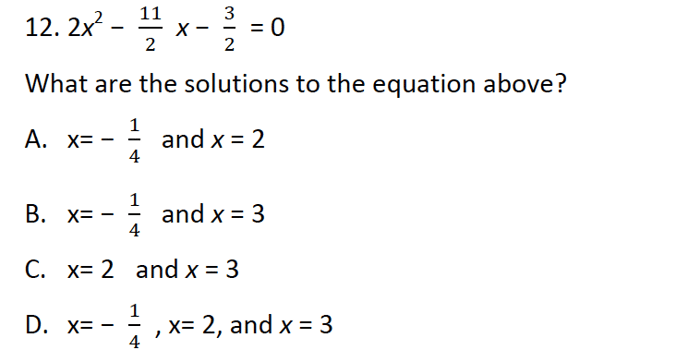
Thông tin cần nhớ
Phương trình bậc 2 có công thức nghiệm tổng quát như sau:

Định lý Viete:
Với phương trình bậc 2: Ta có:
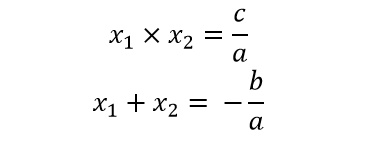
Giải ví dụ
Đối với bài tập này, thí sinh có thể bấm máy tính để giải do đây thuộc phần Toán được sử dụng máy tính.
Tuy nhiên, nếu áp dụng định lý Viete cũng có thể tìm được phương án đúng nhanh:
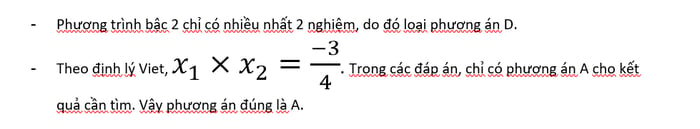
Dạng 2: Xây dựng phương trình bậc hai
Yêu cầu
Dạng bài này yêu cầu thí sinh xác định phương trình bậc 2 từ kết quả nghiệm của chúng. Đây có thể coi là dạng bài ngược lại với dạng bài trước.
Ví dụ
Cùng xem xét câu hỏi dưới đây:
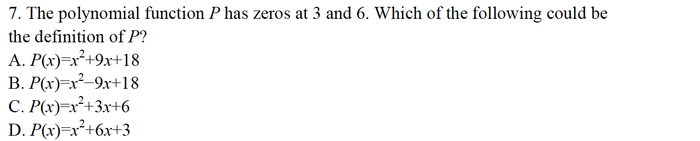
Bí quyết nhớ
Với phương trình bậc 2 nhận là nghiệm. Phương trình đó có thể được viết dưới dạng sau:
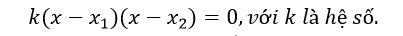
Từ đây, ta có thể tìm được dạng phương trình bậc 2 bằng cách nhân các hiệu của x và nghiệm với nhau, sau đó khai triển bằng quy tắc khai triển đa thức ở phần trên.
Phân tích bài toán ví dụ
Phương trình nhận 3 và 6 là nghiệm, do đó hàm P(x) có thể có dạng như sau:
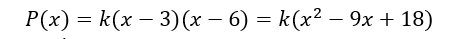
Với k = 1, ta có phương trình giống như phương trình trong phương án B. Các phương án còn lại đều không cho dạng phương trình đúng. Vậy đáp án đúng là B.
Dạng 3: Phân tích đồ thị hàm bậc hai
Điều kiện
Dạng bài này yêu cầu thí sinh tìm hàm ứng với đồ thị cho trước hoặc ngược lại. Ngoài ra có xuất hiện các bài toán về chuyển dịch đồ thị.
Mẫu mực
Cùng xem xét câu hỏi dưới đây:
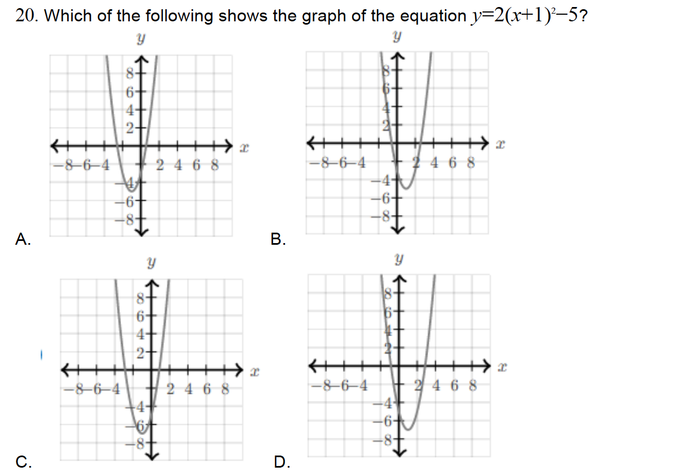
Những kiến thức cần nhớ
Phương trình bậc 2 ax2 + bx + c = 0 (a khác 0) có đồ thị là một đường parabol. Một số quy tắc về dáng điệu của đồ thị:
Với a < 0, đồ thị úp xuống dưới. (Lồi) – Tồn tại giá trị lớn nhất là đỉnh của đồ thị.
Với a > 0, đồ thị quay lên trên. (Lõm) – Tồn tại giá trị nhỏ nhất là đáy của đồ thị.
Đồ thị cắt trục hoành tại điểm là nghiệm của phương trình.
Phương trình có 2 nghiệm: đồ thị cắt trục hoành tại 2 điểm
Phương trình có 1 nghiệm: đồ thị cắt trục hoành tại 1 điểm (cực trị).
Phương trình vô nghiệm: đồ thị không cắt trục hoành.
Toạ độ điểm cực trị (đỉnh/đáy) của phương trình bậc 2 là:

Đồ thị cắt trục tung tại điểm có toạ độ: x=0, y=c
Xử lý các ví dụ
Do phương trình mà đề bài cho thuận lợi cho việc tìm giá trị nhỏ nhất của hàm số, ưu tiên xét điểm đáy (cực tiểu) của đồ thị. Hàm số đạt cực tiểu khi x = -1, y = -5 khi đó Dựa vào đồ thị, dễ dàng xác định được phương án đúng là A với toạ độ của cực tiểu như đã tính toán.
Quy luật mũ, hàm mũ
Phần 1: Quy luật mũ và bài toán tăng trưởng
Yêu cầu
Dạng bài này yêu cầu thí sinh đọc một vấn đề rồi xây dựng hàm, hoặc phân tích hàm biểu diễn cho vấn đề đó. Thí sinh cần hiểu và chỉ ra được mối quan hệ giữa các đối tượng và sự thay đổi của chúng.
Ví dụ minh họa
Cùng xem xét câu hỏi dưới đây:

Kiến thức cần ghi nhớ
Phân biệt hàm mũ và hàm luỹ thừa:
Với hàm mũ, biến số x đóng vai trò làm số mũ, một hằng số nào đó sẽ đóng vai trò làm cơ số. Ví dụ: y= 2x
Với hàm luỹ thừa, biến số x đóng vai trò làm cơ số, một hệ số nào đó sẽ đóng vai trò làm số mũ. Ví dụ: y= x2
Trong các phép toán hỗn hợp có chứa phép cộng trừ nhân chia và lũy thừa, ta ưu tiên thao tác theo thứ tự: lũy thừa => nhân chia => cộng trừ. Trong trường hợp có dấu ngoặc, ưu tiên phép toán trong ngoặc trước.
Chiến lược
Đối với dạng bài toán tăng trưởng và xây dựng hàm biểu diễn như trên, thí sinh có thể áp dụng cách tiếp cận sau đây:
B1: Đọc đề bài, xác định các biến số thay đổi. Xác định đối tượng nào là hàm, đối tượng nào là biến.
B2: Cho đối tượng biến thay đổi (chú ý chọn những mốc đặc biệt hoặc dễ tính toán), và xem sự thay đổi của đối tượng làm hàm. Xác định mối quan hệ là tuyến tính hay luỹ thừa (cấp số nhân), là tỷ lệ thuận hay nghịch.
B3: Loại trừ các phương án không phù hợp.
Giải quyết một ví dụ
Đề bài hỏi đâu là mối quan hệ giữa Hiệu điện thế (v, tính theo t) và thời gian (t, tính theo phút). Xét thời điểm đầu, khi t = 0, v = 0,41. Chọn khi t = 5/2, v = 0,41 x 0,8. Chọn khi t = 10/2, v = 0,41 x 0,82
Từ đó, rút ra rằng sau mỗi khoảng thời gian là t = 5/2 =2,5 (s), hiệu điện thế v lại giảm xuống còn 0,8 lần giá trị trước đó.
Vì đây là hàm mũ nên loại hai phương án A và B (linear tức là tuyến tính). Với kết quả đã phân tích ở trên, phương án đúng là C. Phương án C sai vì hiệu điện thế giảm chứ không tăng.
Phần 2: Biến đổi các biểu thức có lũy thừa
Điều kiện
Dạng bài này yêu cầu thí sinh biến đổi và rút gọn các biểu thức chứa luỹ thừa.
Mẫu mực
Cùng xem xét câu hỏi dưới đây:

Kiến thức cần ghi nhớ
Quy tắc nhân chia luỹ thừa:
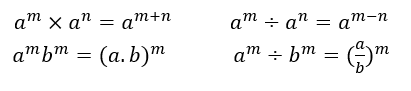
Xử lý các ví dụ
Áp dụng quy tắc trong phần kiến thức cần nhớ, có:
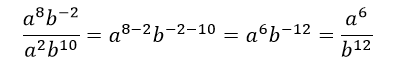
Vậy đáp án đúng là D.
Dạng 3: Giải phương trình căn bậc hai
Ví dụ minh họa
Cùng xem xét câu hỏi dưới đây:

Chiến lược
Đối với các bài toán chứa căn thức, thí sinh có thể giải bằng cách tiếp cận sau đây:
Chuyển vế, đổi dấu. Đưa biểu thức có chứa căn về một bên của dấu bằng, đưa các số hạng còn lại vào bên còn lại. (Đặt điều kiện cho biểu thức ở vế không có căn thức lớn hơn hoặc bằng 0).
Bình phương hai vế, chuyển thành dạng phương trình bậc 2.
Giải phương trình bậc 2 và tìm nghiệm thoả mãn.
Xử lý các ví dụ
Điều kiện xác định của phương trình là: p+2 ≥ 0 p ≥ – 2.
Bình phương hai vế của phương trình, có:
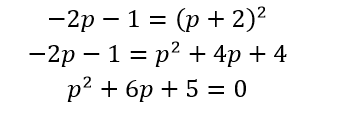
Từ đây, suy ra x = –1 và x = –5, tuy nhiên đáp án x = – 5 không thoả mãn điều kiện xác định nên phương trình chỉ có 1 nghiệm x= –1. Vậy tổng các nghiệm thỏa mãn là –1. (Đáp án C).
Lưu ý: thí sinh cần xác định được hai nghiệm của phương trình rồi kiểm tra với điều kiện xác định. Dù sử dụng định lý Viete có thể cho kết quả nhanh hơn nhưng có thể cho đáp án sai vì có thể xuất hiện nghiệm không thỏa mãn điều kiện xác định như ví dụ trên.
Phương trình tỉ số
Dạng 1: Thực hiện phép cộng trừ trên hàm phân thức
Mẫu minh họa
Cùng xem xét câu hỏi dưới đây:
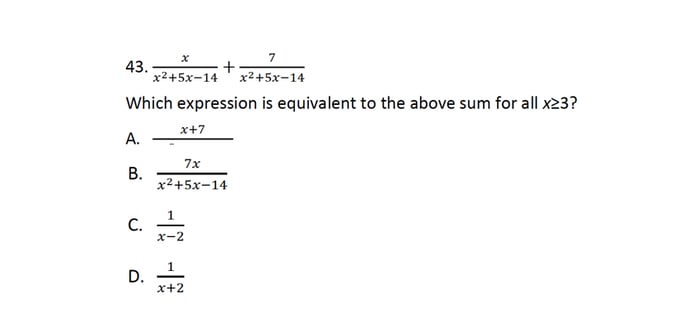
Chú ý
Đối với những bài tập này, bên cạnh việc thao tác các phép tính, thí sinh cũng cần phân tích đa thức ở tử và mẫu thành nhân tử khi có thể để đưa phân số về dạng tối giản theo đề bài.
Xử lý các ví dụ
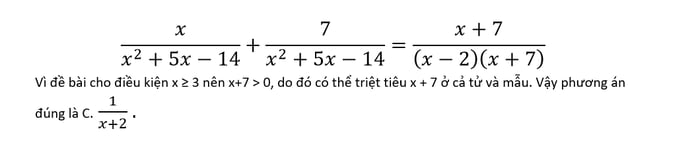
Phương pháp biểu diễn đơn giản biểu thức
Mẫu minh họa
Cùng xem xét câu hỏi dưới đây:
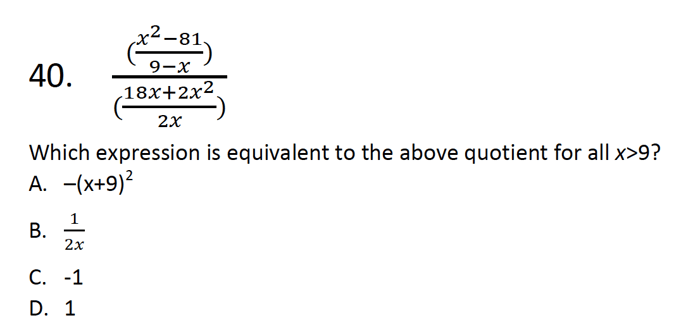
Chiến lược
Phân tích các thành phần đa thức thành nhân tử rồi triệt tiêu những nhân tử có thể, trước khi thực hiện tính toán.
Rút gọn phân thức đến tối giản và chú ý điều kiện xác định của đề bài.
Xử lý các ví dụ
Do đây là một phân số khá phức tạp nên việc xét riêng tử số và mẫu số trước là một ý tưởng tốt. Xét tử số, có:
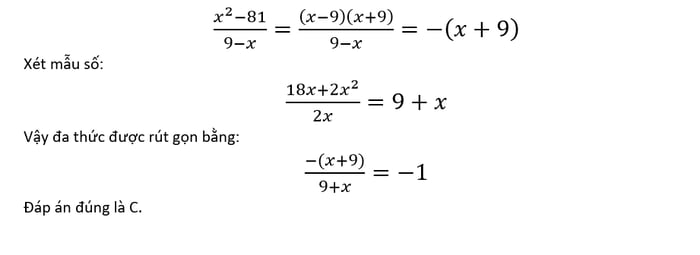
Các chủ đề khác trong Toán SAT
Hình học
Lượng giác trong hình học
Ví dụ
Cùng xem xét câu hỏi dưới đây:
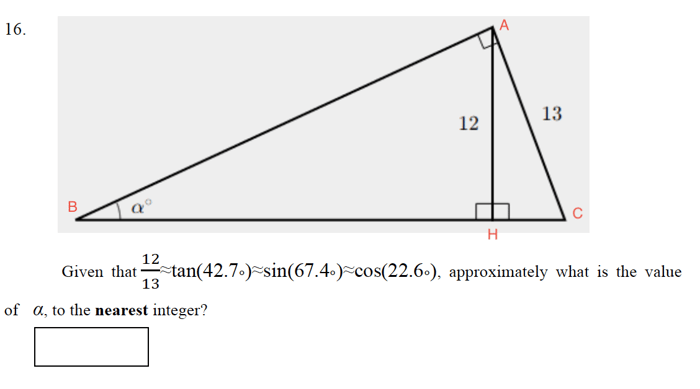
Kiến thức cần biết
Các tỉ số sin, cos, tan, cot trong hình học.
Định lý về tam giác, tam giác đồng dạng, bằng nhau.
(Chương trình lớp 9, THCS)
Giải thích ví dụ
Góc ∝ Xét ΔABH và ΔCAH, có: góc BAH = góc ACH, góc AHB = góc CHA = 90º. Suy ra ΔABH và ΔCAH đồng dạng. => Góc ABH = ∝ = góc HAC.
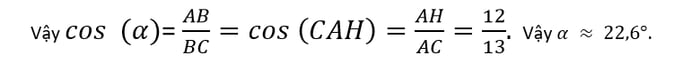
Hình học phẳng
Ví dụ
Cùng xem xét câu hỏi dưới đây:
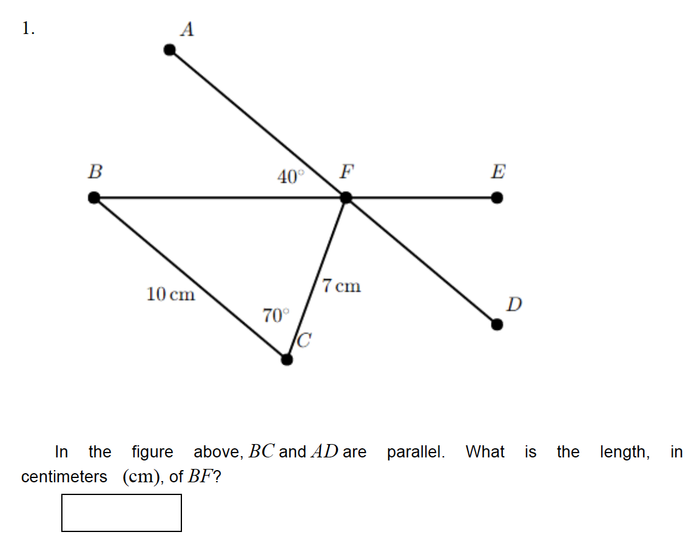
Kiến thức cần phải biết
Định lý các đường vuông góc, song song.
Góc đối, góc kề, kề bù, đồng bị, trong cùng phía,…
Tam giác đồng dạng, tam giác bằng nhau, tổng các góc trong tam giác,…
(Chương trình hình học lớp 8-9, THCS)
Giải thích ví dụ
Vì BC và AD song song nên góc CBF = góc BFA = 40º. Xét tam giác CBF ∠C+∠B+∠BFC=180°⇒ ∠BFC=180-70-40=70°. Suy ra góc BFC = góc BCF, vậy tam giác BFC cân tại B. Suy ra BC = BF = 10cm. Vậy độ dài BF là 10cm.
Hình không gian
Ví dẫn minh
Cùng xem xét câu hỏi dưới đây:
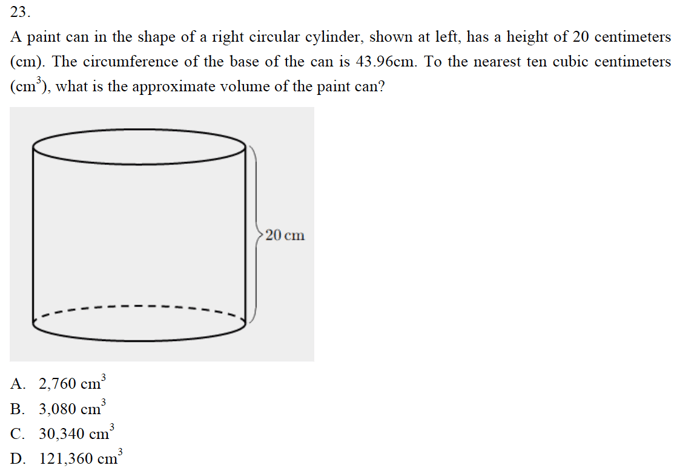
Kiến thức cần nắm
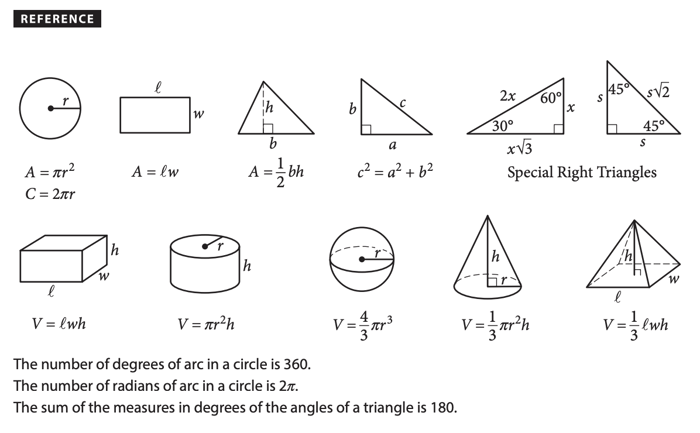
Các công thức về hình học được in ở bìa của phần Math Section trong đề thi của College Board. Thí sinh có thể tham khảo dạng các công thức được công thức ở trang đó để làm bài.
Giải quyết bài toán mẫu
Đề bài yêu cầu tính thể tích của khối trụ. Chiều cao khối trụ được cho trước là 20cm. Chu vi của đáy trụ được cho là 43,96 cm. Theo công thức, thể tích hình trụ là V = S.h. Do đó cần xác định diện tích đáy trụ.
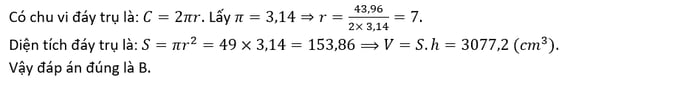
Hệ trục tọa độ
Minh họa
Cùng xem xét câu hỏi dưới đây:

Kiến thức CẦN THIẾT
Với các bài toán về toạ độ, thí sinh cần vận dụng lý thuyết hình học tọa độ (hình học 10 – 11, bậc THPT). Một số lý thuyết thường gặp là phương trình đường tròn, đồ thị đa thức bậc cao, … Các dạng bài này kiểm tra kiến thức ở mức độ cơ bản.
Bài toán mẫu
Đường tròn có đường kính có 2 điểm đầu mút là A(0,3) và B(– 4,0). Từ dữ kiện này, có thể tìm được 2 giá trị quan trọng là: toạ độ tâm đường tròn – là trung điểm AB – và độ dài đường kính.
Trong hệ toạ độ, toạ độ trung điểm M của đoạn thẳng AB được tính như sau:
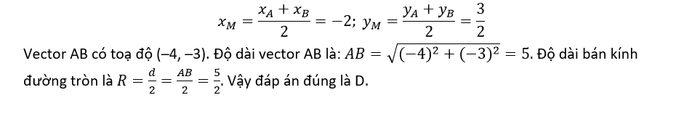
Số phức
Minh họa
Cùng xem xét câu hỏi dưới đây:

Kiến thức cần biết
Định nghĩa về số phức
Thao tác biến đổi số phức
(Chương trình đại số lớp 12 – THPT).
Xử lý ví dụ
Để chuyển đổi một phân số có tử và mẫu số là số phức thành dạng chỉ có tử số là số phức, thí sinh áp dụng phương pháp nhân tử và mẫu số với số phức nghịch đảo của mẫu số.
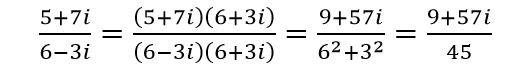
Vậy câu trả lời đúng là A.
