1. Giải phương trình lượng giác Sin x = a
1. Nếu |a| lớn hơn 1 thì phương trình không có nghiệm.
2. Nếu |a| nhỏ hơn hoặc bằng 1, chọn góc α sao cho sinα = a
Khi đó, (sin x = sin alpha)
x = alpha + k cdot 2pi quad (k in mathbb{Z})
x = pi - alpha + k cdot 2pi quad (k in mathbb{Z})
Các tình huống đặc biệt
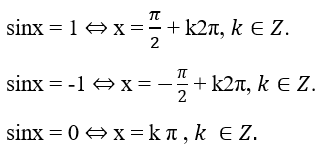
2. Phương pháp giải phương trình lượng giác (cos x = a)
Nếu (|a| > 1), thì phương trình (cos(alpha) = a) không có nghiệm trong khoảng giá trị của (alpha) vì giá trị của hàm cosinus chỉ dao động từ -1 đến 1. Do đó, khi (|a| > 1), không có giá trị nào của (alpha) để (cos(alpha) = a)
Nếu (|a| leq 1), nghĩa là (a) nằm trong khoảng từ -1 đến 1 (bao gồm cả -1 và 1), thì tồn tại giá trị của (alpha) sao cho (cos(alpha) = a). Để tìm (alpha), bạn có thể sử dụng hàm nghịch đảo của cosinus (hay còn gọi là hàm arccos hoặc inverse cosine).
Cụ thể: (alpha = arccos(a)). Giá trị của (alpha) sẽ nằm trong khoảng từ 0 đến (pi) (hoặc từ 0 đến 180 độ) nếu (a) dương và từ 0 đến (pi) (hoặc từ 0 đến -180 độ) nếu (a) âm
Nhớ rằng các phương trình lượng giác có thể có nhiều nghiệm, không chỉ một nghiệm duy nhất, tùy thuộc vào giá trị của (a) và khoảng giá trị của (alpha).
Khi đó, (cos x = a)
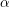
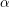
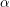

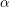

3. Phương pháp giải phương trình lượng giác ( an x = a)
Chọn góc (alpha) sao cho ( an alpha = a).
Khi đó, phương trình ( an x = a) được giải.
( an x = an alpha)
(Rightarrow x = alpha + k cdot pi quad (k in mathbb{Z}))
(alpha = arctan(a)). Giá trị của (alpha) được xác định bởi hàm tang (hay còn gọi là hàm tangent nghịch đảo) và nằm trong khoảng từ (- rac{pi}{2}) đến ( rac{pi}{2}) (hoặc từ -90 độ đến 90 độ).
Do đó, phương trình ( an(x) = an(alpha)) có nghiệm là (x = alpha + k cdot pi) với (k) là số nguyên.
Điều này hoàn toàn chính xác. Phương trình ( an(x) = an(alpha)) có nghiệm khi giá trị của (x) và (alpha) thuộc cùng một khoảng của hàm tang.
Vì hàm tang có chu kỳ (pi), các nghiệm của nó sẽ lặp lại theo chu kỳ này.
x = alpha + k cdot pi quad (k ext{ là số nguyên bất kỳ})
Ví dụ: Nếu (alpha = rac{4}{pi}), thì các giá trị của (x) thỏa mãn ( an(x) = anleft( rac{4}{pi} ight)) là (x = rac{4}{pi} + k cdot pi), với (k) là số nguyên bất kỳ.
4. Phương pháp giải phương trình lượng giác (cot x = a)
(cot x = cot a)

(cot x = a)

Các tình huống đặc biệt
(cot x = 0 Leftrightarrow x = rac{pi}{2} + k cdot pi quad (k in mathbb{Z}))
(cot x = pm 1 Leftrightarrow x = pm rac{pi}{4} + k cdot pi quad (k in mathbb{Z}))
5. Một số bài tập cơ bản về phương trình lượng giác
Bài 1: Phương trình (cos 2x = 1) có nghiệm là:
A. (x = k cdot pi, k in mathbb{Z}).
B. (x = k cdot rac{pi}{2}, k in mathbb{Z}).
C. (x = k cdot rac{pi}{3}, k in mathbb{Z})
D. (x = k cdot rac{pi}{4}, k in mathbb{Z})
Bài 2: Phương trình ( anleft(x - rac{pi}{4} ight) = 0) có nghiệm là:
A. (x = rac{pi}{4} + k cdot pi, k in mathbb{Z})
B. (x = rac{3pi}{4} + k cdot pi, k in mathbb{Z})
C. (x = k cdot pi, k in mathbb{Z})
D. (x = k cdot 2pi, k in mathbb{Z})
Bài 3: Phương trình (cotleft(x + rac{pi}{4} ight) = 0) có nghiệm là:
A. (x = - rac{pi}{4} + k cdot pi, k in mathbb{Z})
B. (x = rac{pi}{4} + k cdot pi, k in mathbb{Z})
C. (x = - rac{pi}{4} + k cdot 2pi, k in mathbb{Z})
D. (x = rac{pi}{4} + k cdot 2pi, k in mathbb{Z})
Bài 4: Trong khoảng ([0; 2pi)), phương trình (sin 2x + sin x = 0) có số nghiệm là:
A. 1
B. 2
C. 3
D. 4
Bài 4: Số nghiệm của phương trình (sinleft(x + rac{pi}{4} ight) = 1) trong khoảng ([0; 3pi]) là:
A. 1
B. 0
C. 2
D. 3
Bài 5: Số nghiệm của phương trình (sin x = cos x) trong khoảng ([0; pi]) là:
A. 1
B. 4
C. 5
D. 2
Bài 6: Phương trình (sin 2x = 1) có nghiệm là gì?
Bài 7: Phương trình (sin(pi cos^2 x) = 1) có nghiệm là gì?
Bài 8: Với những giá trị nào của (x) thì hai hàm số (y = sin 3x) và (y = sin x) có giá trị bằng nhau?
6. Tại sao học sinh thường gặp khó khăn khi làm bài tập lượng giác cơ bản?
Có một số lý do chính khiến học sinh hay gặp khó khăn với bài tập lượng giác cơ bản:
Phức tạp của công thức: Các công thức lượng giác có thể rất phức tạp và dễ gây nhầm lẫn. Việc ghi nhớ và áp dụng chúng một cách chính xác có thể gặp khó khăn. Thay vì chỉ nhớ công thức, hãy cố gắng hiểu cách chúng hoạt động. Hiểu nguyên lý đằng sau công thức và cách chúng giúp giải bài toán sẽ giúp bạn ghi nhớ lâu hơn và áp dụng tự tin hơn. Khi gặp bài toán lượng giác, hãy thử phân tích và vẽ hình minh họa, điều này thường giúp bạn hiểu rõ hơn về vấn đề.
Kết hợp đại số và lượng giác: Trong nhiều bài tập, học sinh cần kết hợp kiến thức đại số với lượng giác, điều này làm tăng độ khó của bài tập.
Khái niệm góc và đơn vị đo góc: Một số học sinh có thể gặp khó khăn trong việc hiểu khái niệm góc và các đơn vị đo góc như radian và độ.
Khả năng hiểu và áp dụng: Lượng giác yêu cầu khả năng nắm bắt và áp dụng kiến thức vào thực tế. Học sinh có thể gặp khó khăn khi cần dùng lượng giác để giải quyết các vấn đề thực tiễn hoặc bài toán phức tạp.
Thiếu thời gian và luyện tập: Đôi khi, lượng giác cơ bản không được luyện tập đủ do thời gian giảng dạy hạn chế, điều này có thể làm cho học sinh thiếu thực nghiệm và tự tin khi làm bài tập.
Thiếu hiểu biết về ý nghĩa hình học: Lượng giác thường gắn liền với hình học, đặc biệt là trong tam giác vuông. Nếu học sinh không hiểu rõ ý nghĩa hình học của các hàm lượng giác, họ sẽ gặp khó khăn khi áp dụng vào bài toán.
Để khắc phục những khó khăn này, học sinh cần thực hành thường xuyên, nắm vững các khái niệm cơ bản và biết cách áp dụng chúng vào bài tập và vấn đề thực tế. Nên tìm sự hỗ trợ từ giáo viên hoặc các tài liệu bổ sung như sách, video hướng dẫn và bài giảng trực tuyến để củng cố kiến thức lượng giác. Một số phương pháp cơ bản có thể giúp bao gồm:
+ Nắm vững các quy tắc cơ bản: Hãy chú trọng vào việc hiểu và nhớ các công thức cơ bản trước. Những công thức này thường là nền tảng để phát triển các công thức phức tạp hơn.
+ Sử dụng hình vẽ và minh họa: Hình vẽ và minh họa giúp bạn dễ dàng hình dung cách các góc và các yếu tố trong bài toán liên quan đến nhau, từ đó áp dụng công thức một cách trực quan hơn.
+ Luyện tập thường xuyên: Thực hành là cách hiệu quả nhất để làm quen với các công thức lượng giác. Giải nhiều bài tập giúp củng cố kiến thức về các công thức, quy tắc và đặc điểm của lượng giác. Việc này giúp bạn tự tin và thành thạo hơn trong việc áp dụng chúng vào các tình huống thực tế, đặc biệt trong việc giải quyết các vấn đề hình học và toán học.
+ Sử dụng công cụ tính toán: Trong một số tình huống, máy tính hoặc ứng dụng có thể hỗ trợ bạn trong việc tính toán và kiểm tra kết quả một cách nhanh chóng và chính xác hơn.
+ Học cách suy luận công thức: Thay vì chỉ nhớ thuộc lòng các công thức, hãy học cách suy luận chúng từ các công thức cơ bản và quy tắc. Kỹ năng này giúp bạn hiểu sâu hơn về lượng giác và tự tin hơn khi giải quyết bài tập.
Hy vọng rằng những thông tin chúng tôi cung cấp sẽ giúp bạn có thêm nguồn kiến thức về giải phương trình lượng giác cơ bản. Những nội dung này sẽ hỗ trợ bạn học tốt hơn và áp dụng phương pháp học hợp lý.
