Trong toán học và khoa học máy tính, một giải thuật, còn gọi là phương pháp giải thuật, là một tập hợp hữu hạn các hướng dẫn được xác định rõ ràng, có thể thực hiện được bằng máy tính, thường để giải quyết một lớp vấn đề hoặc để thực hiện một phép tính. Các giải thuật luôn rõ ràng và được sử dụng chỉ rõ việc thực hiện các phép tính, xử lý dữ liệu, suy luận tự động và các tác vụ khác.
Là một phương pháp hiệu quả, một giải thuật có thể được biểu diễn trong một khoảng không gian và thời gian hữu hạn, và bằng một ngôn ngữ hình thức được xác định rõ ràng để tính toán một hàm số. Bắt đầu từ trạng thái ban đầu và đầu vào ban đầu (có thể trống), các hướng dẫn mô tả một phép tính, khi được thực thi, sẽ tiến hành qua một số hữu hạn các trạng thái kế tiếp được xác định rõ, cuối cùng tạo ra 'đầu ra' và chấm dứt ở trạng thái kết thúc cuối cùng. Sự chuyển đổi từ trạng thái này sang trạng thái tiếp theo không nhất thiết phải mang tính xác định; một số thuật toán, được gọi là thuật toán ngẫu nhiên, kết hợp đầu vào ngẫu nhiên.
Khái niệm giải thuật đã tồn tại từ thời cổ đại. Các giải thuật số học, chẳng hạn như giải thuật chia, được sử dụng bởi các nhà toán học Babylon cổ đại vào khoảng 2500 TCN và các nhà toán học Ai Cập vào khoảng 1550 TCN. Các nhà toán học Hy Lạp sau đó đã sử dụng các giải thuật trong sàng Eratosthenes để tìm số nguyên tố, và giải thuật Euclide để tìm ước chung lớn nhất của hai số. Các nhà toán học Ả Rập như al-Kindi vào thế kỷ thứ 9 đã sử dụng các giải thuật mật mã để phá mã, dựa trên phân tích tần số.
Thuật toán bắt nguồn từ nhà toán học thế kỷ thứ 9 Muḥammad ibn Mūsā al-Khwārizmī, tên ông được Latinh hóa thành Algoritmi. Việc chính thức hóa một phần những gì sẽ trở thành khái niệm thuật toán hiện đại bắt đầu với nỗ lực giải Entscheidungsproblem (vấn đề quyết định) do David Hilbert đặt ra vào năm 1928. Các công thức hóa sau này được đóng khung như những nỗ lực để xác định 'khả năng tính toán hiệu quả' hoặc 'phương pháp hiệu quả'. Những công thức hóa đó bao gồm các hàm đệ quy Gödel - Herbrand - Kleene của các năm 1930, 1934 và 1935, phép tính lambda của Alonzo Church năm 1936, Công thức 1 của Emil Post năm 1936 và các máy Turing của Alan Turing năm 1936–37 và 1939.
Định nghĩa không chính thức
Một định nghĩa không chính thức có thể là 'một tập hợp các quy tắc xác định chính xác một chuỗi hoạt động', mà sẽ bao gồm tất cả các chương trình máy tính (bao gồm cả các chương trình không thực hiện phép tính số) và (ví dụ) bất kỳ thủ tục hành chính quy định nào hoặc công thức nấu ăn.
Nói chung, một chương trình chỉ là một thuật toán nếu cuối cùng nó dừng lại - mặc dù các vòng lặp vô hạn đôi khi có thể chấp nhận được.
Một ví dụ nguyên mẫu của một thuật toán là thuật toán Euclid, được sử dụng để xác định ước chung lớn nhất của hai số nguyên; một ví dụ được mô tả bằng lưu đồ ở trên và là ví dụ trong phần sau.
Boolos, Jeffrey & 1974, 1999 đưa ra một định nghĩa không chính thức cho thuật toán như sau:
- Không một con người nào có thể viết đủ nhanh, đủ dài, hoặc đủ nhỏ (nhỏ hơn và nhỏ hơn mà không có giới hạn... bạn đang cố viết trên phân tử, trên nguyên tử, trên electron) để liệt kê tất cả các thành viên của vô số thiết lập bằng cách viết ra tên của họ, cái khác, trong một số ký hiệu. Nhưng con người có thể làm điều gì đó hữu ích không kém, trong trường hợp có nhiều tập hợp vô hạn nhất định: Họ có thể đưa ra các chỉ dẫn rõ ràng để xác định phần tử thứ n của tập hợp, cho n hữu hạn tùy ý. Những hướng dẫn như vậy phải được đưa ra khá rõ ràng, dưới hình thức mà chúng có thể được tuân theo bởi một máy tính toán hoặc bởi một con người chỉ có khả năng thực hiện các thao tác rất cơ bản trên các ký hiệu.
'Tập hợp vô hạn liệt kê được' là tập hợp mà các phần tử của nó có thể được song ánh tương ứng 1-1 với các số nguyên. Vì vậy, Boolos và Jeffrey đang nói rằng một thuật toán ngụ ý hướng dẫn cho một quá trình 'tạo' các số nguyên đầu ra từ một số nguyên 'đầu vào' tùy ý hoặc các số nguyên, theo lý thuyết, có thể lớn tùy ý. Ví dụ: một thuật toán có thể là một phương trình đại số chẳng hạn như y = m + n (tức là hai 'biến đầu vào' tùy ý m và n tạo ra đầu ra y), nhưng các nỗ lực của các tác giả khác nhau để xác định khái niệm cho thấy rằng từ đó ngụ ý nhiều hơn thế này, một cái gì đó theo thứ tự của (cho ví dụ bổ sung):
- Các hướng dẫn chính xác (bằng ngôn ngữ mà 'máy tính' hiểu được) để có một quy trình 'tốt' nhanh, hiệu quả, chỉ định các 'động thái' của 'máy tính' (máy hoặc con người, được trang bị bên trong thông tin và khả năng) để tìm, giải mã và sau đó xử lý các số nguyên / ký hiệu đầu vào tùy ý m và n, ký hiệu + và = … và 'hiệu quả'
sản xuất ra, trong một thời gian 'hợp lý', đầu ra-số nguyên y tại một nơi được chỉ định và với định dạng được chỉ định.
Khái niệm thuật toán cũng được áp dụng để định nghĩa khái niệm về khả năng giải mã — một khái niệm trung tâm để giải thích cách các hệ thống hình thức ra đời bắt đầu từ một tập hợp nhỏ các tiên đề và quy tắc. Về mặt logic, thời gian mà một thuật toán yêu cầu để hoàn thành không thể đo được, vì nó dường như không liên quan đến kích thước vật lý thông thường. Từ sự không chắc chắn như vậy, đặc trưng cho công việc đang diễn ra, dẫn đến việc không có định nghĩa thuật toán phù hợp với cả cách sử dụng thuật ngữ này một cách cụ thể (theo một nghĩa nào đó)
Hình thức hóa
Các thuật toán rất cần thiết cho cách máy tính xử lý dữ liệu. Nhiều chương trình máy tính chứa các thuật toán trình bày chi tiết các hướng dẫn cụ thể mà máy tính phải thực hiện — theo một thứ tự cụ thể — để thực hiện một nhiệm vụ cụ thể, chẳng hạn như tính tiền lương của nhân viên hoặc in phiếu điểm của học sinh. Vì vậy, một thuật toán có thể được coi là bất kỳ chuỗi hoạt động nào có thể được mô phỏng bởi một hệ thống hoàn chỉnh Turing. Các tác giả khẳng định luận điểm này bao gồm Minsky (1967), Savage (1987) và Gurevich (2000):
- Minsky: 'Nhưng chúng tôi cũng sẽ duy trì, với Turing... rằng bất kỳ thủ tục nào có thể' tự nhiên 'được gọi là hiệu quả, trên thực tế, có thể được thực hiện bởi một chiếc máy (đơn giản). Mặc dù điều này có vẻ cực đoan, nhưng những lập luận… ủng hộ nó thì khó có thể bác bỏ ”.
- Gurevich: “… Lập luận không chính thức của Turing ủng hộ luận điểm của ông ấy biện minh cho luận điểm mạnh mẽ hơn: mọi thuật toán đều có thể được mô phỏng bởi máy Turing… theo Savage [1987], thuật toán là một quá trình tính toán được xác định bởi máy Turing'.
Máy Turing có thể xác định các quy trình tính toán không kết thúc. Các định nghĩa không chính thức của thuật toán thường yêu cầu thuật toán luôn kết thúc. Yêu cầu này làm cho nhiệm vụ quyết định xem một thủ tục chính thức có phải là một thuật toán không trong trường hợp chung - do một định lý chính của lý thuyết tính toán được gọi là bài toán dừng.
Thông thường, khi một thuật toán được liên kết với xử lý thông tin, dữ liệu có thể được đọc từ nguồn đầu vào, được ghi vào thiết bị đầu ra và được lưu trữ để xử lý thêm. Dữ liệu được lưu trữ được coi là một phần của trạng thái bên trong của thực thể thực hiện thuật toán. Trong thực tế, trạng thái được lưu trữ trong một hoặc nhiều cấu trúc dữ liệu.
Đối với một số quá trình tính toán này, thuật toán phải được xác định chặt chẽ: được chỉ định theo cách nó áp dụng trong mọi trường hợp có thể phát sinh. Điều này có nghĩa là mọi bước có điều kiện phải được xử lý một cách có hệ thống, theo từng trường hợp cụ thể; các tiêu chí cho từng trường hợp phải rõ ràng (và có thể tính toán được).
Bởi vì một thuật toán là một danh sách chính xác của các bước chính xác, thứ tự tính toán luôn quan trọng đối với hoạt động của thuật toán. Các hướng dẫn thường được giả định là được liệt kê rõ ràng và được mô tả là bắt đầu 'từ trên cùng' và đi 'xuống dưới cùng' — một ý tưởng được mô tả chính thức hơn bằng luồng kiểm soát.
Cho đến nay, cuộc thảo luận về việc chính thức hóa một thuật toán đã giả định các tiền đề của lập trình mệnh lệnh. Đây là quan niệm phổ biến nhất - một quan niệm cố gắng mô tả một nhiệm vụ bằng các phương tiện 'máy móc', rời rạc. Duy nhất cho quan niệm về các thuật toán chính thức hóa này là phép toán gán, đặt giá trị của một biến. Nó bắt nguồn từ trực giác của 'bộ nhớ' như một bàn di chuột. Dưới đây là một ví dụ về sự phân công như vậy.
Đối với một số quan niệm thay thế về những gì tạo thành một thuật toán, hãy xem lập trình hàm và lập trình logic.
Diễn đạt thuật toán
Các thuật toán có thể được biểu diễn bằng nhiều loại ký hiệu, bao gồm ngôn ngữ tự nhiên, mã giả, lưu đồ, biểu đồ drakon, ngôn ngữ lập trình hoặc bảng điều khiển (được xử lý bởi trình thông dịch). Biểu diễn bằng ngôn ngữ tự nhiên của các thuật toán có thể rất dài dòng và mơ hồ, ít khi được sử dụng cho các thuật toán phức tạp hoặc kỹ thuật. Mã giả, lưu đồ, biểu đồ drakon và bảng điều khiển là các cách có cấu trúc để biểu diễn các thuật toán, tránh được nhiều sự mơ hồ thường gặp trong các câu lệnh dựa trên ngôn ngữ tự nhiên. Ngôn ngữ lập trình chủ yếu dùng để biểu diễn các thuật toán dưới dạng có thể thực thi bởi máy tính, nhưng cũng thường được dùng làm cách để định nghĩa hoặc tài liệu hóa các thuật toán.
Có nhiều cách biểu diễn khác nhau và một chương trình máy Turing cụ thể có thể được biểu diễn dưới dạng chuỗi bảng máy (xem máy trạng thái hữu hạn, bảng chuyển đổi trạng thái và bảng điều khiển để biết thêm), lưu đồ và biểu đồ drakon (xem biểu đồ trạng thái để biết thêm), hoặc dưới dạng mã máy thô sơ hoặc mã lắp ráp được gọi là 'bộ tứ' (xem máy Turing để biết thêm).
Đại diện của thuật toán có thể được phân loại thành ba cấp độ chấp nhận được của mô tả máy Turing như sau:
- 1. Mô tả cấp cao
- '... Văn bản dùng để mô tả một thuật toán, bỏ qua các chi tiết thực thi. Ở cấp độ này, không cần phải đề cập đến cách máy quản lý băng hoặc đầu vào của nó.'
- 2. Mô tả thực thi
- '... Văn bản được dùng để xác định cách máy Turing sử dụng đầu vào và cách nó lưu trữ dữ liệu trên băng của mình. Ở cấp độ này, không cần cung cấp thông tin chi tiết về các trạng thái hoặc chức năng chuyển tiếp.'
- 3. Mô tả chính thức
- Mức chi tiết nhất, 'mức thấp nhất', đưa ra 'bảng trạng thái' của máy Turing.
Thiết kế
Thiết kế thuật toán đề cập đến phương pháp hoặc quy trình toán học để giải quyết vấn đề và các thuật toán kỹ thuật. Việc thiết kế các thuật toán là một phần của nhiều lý thuyết giải pháp nghiên cứu hoạt động, như lập trình động và chia để trị. Các kỹ thuật thiết kế và triển khai thiết kế thuật toán còn được gọi là mẫu thiết kế thuật toán, với các ví dụ như mẫu phương pháp và mẫu trang trí.
Một trong những khía cạnh quan trọng nhất của thiết kế thuật toán là tạo ra thuật toán có thời gian chạy hiệu quả, được gọi là Big O của nó.
Các bước điển hình trong quá trình phát triển thuật toán:
- Định nghĩa vấn đề
- Phát triển một mô hình
- Đặc điểm kỹ thuật của thuật toán
- Thiết kế một thuật toán
- Kiểm tra tính đúng đắn của thuật toán
- Phân tích thuật toán
- Thực hiện thuật toán
- Chương trình thử nghiệm
- Viết tài liệu
Thực hiện
Enaliarctos
Hầu hết các thuật toán được thiết kế để thực hiện như các chương trình máy tính. Tuy nhiên, các thuật toán cũng có thể được thực hiện bằng các phương tiện khác như trong mạng nơ-ron sinh học (ví dụ, não người thực hiện phép tính số học hoặc côn trùng đang tìm kiếm thức ăn), trong mạch điện hoặc trong một thiết bị cơ khí.
Thuật toán máy tính
{{{1}}}) (hình thoi), GOTO không điều kiện (hình chữ nhật), các toán tử gán khác nhau (hình chữ nhật) và HALT (hình chữ nhật). Sự nhúng các cấu trúc này vào trong các khối gán dẫn đến các sơ đồ phức tạp (xem Tausworthe 1977: 100, 114).Trong các hệ thống máy tính, thuật toán cơ bản là một ví dụ của logic được viết trong phần mềm bởi các nhà phát triển phần mềm, nhằm hiệu quả hóa máy tính 'đích' để tạo ra đầu ra từ đầu vào nhất định (có thể là rỗng). Một thuật toán tối ưu, thậm chí chạy trên phần cứng cũ, sẽ đem lại kết quả nhanh hơn so với thuật toán không tối ưu (với độ phức tạp thời gian cao hơn) cho cùng mục đích, chạy trên phần cứng hiệu quả hơn; đó là lý do vì sao các thuật toán, giống như phần cứng máy tính, được coi là công nghệ.
Chương trình 'thanh lịch' (nhỏ gọn), chương trình 'tốt' (nhanh): Khái niệm 'đơn giản và thanh lịch' không chính thức được đề cập đến ở Knuth và chính xác là ở Chaitin:
- Knuth: '… chúng tôi muốn có các thuật toán tốt theo một khía cạnh thẩm mỹ được xác định lỏng lẻo. Một tiêu chí… là khoảng thời gian thực hiện thuật toán…. Các tiêu chí khác là khả năng thích ứng của thuật toán với máy tính, tính đơn giản và sang trọng của nó, v.v. '
- Chaitin: '… một chương trình là 'thanh lịch', theo ý tôi thì đó là chương trình nhỏ nhất có thể để tạo ra kết quả đầu ra mà nó thực hiện'
Chaitin bắt đầu định nghĩa của mình với: 'Tôi sẽ cho bạn thấy rằng bạn không thể chứng minh rằng một chương trình là 'thanh lịch '' — ví dụ như việc chứng minh bài toán dừng (ibid).
Thuật toán so với hàm có thể tính toán bằng nhiều thuật toán khác nhau: Đối với một hàm đã cho, có nhiều thuật toán khác nhau có thể tồn tại. Điều này đúng ngay cả khi không mở rộng tập lệnh có sẵn cho lập trình viên. Rogers lưu ý rằng “Quan trọng là phải phân biệt giữa khái niệm thuật toán, tức là thủ tục và khái niệm hàm có thể tính toán bằng thuật toán, tức là ánh xạ được tạo ra bởi thủ tục. Cùng một chức năng có thể có nhiều thuật toán khác nhau '.
Rất tiếc, có thể xảy ra sự cân bằng giữa tính tốt (tốc độ) và tính thanh lịch (nhỏ gọn)—một chương trình thanh lịch có thể cần nhiều bước hơn để hoàn thành một phép tính so với một chương trình ít thanh lịch hơn. Ví dụ sử dụng thuật toán Euclid được đề cập dưới đây.
Máy tính, các mô hình tính toán: Máy tính (hoặc 'máy tính' của con người) là một loại máy bị hạn chế, một 'thiết bị cơ khí xác định rời rạc' làm theo hướng dẫn mù quáng của nó. Các mô hình đơn giản của Melzak và Lambek chia nhỏ khái niệm này thành bốn yếu tố: (i) các vị trí rời rạc, dễ phân biệt, (ii) các bộ đếm rời rạc, không thể phân biệt được (iii) một tác nhân và (iv) một danh sách hướng dẫn có hiệu quả so với khả năng của tác nhân.
Minsky mô tả một biến thể thích hợp hơn của mô hình 'bàn tính' của Lambek trong 'Các cơ sở rất đơn giản để tính toán' của ông. Máy của Minsky thực hiện tuần tự qua năm (hoặc sáu, tùy thuộc vào cách đếm) lệnh, trừ khi IF – THEN GOTO có điều kiện hoặc GOTO không điều kiện thay đổi luồng chương trình. Bên cạnh HALT, máy của Minsky bao gồm ba hoạt động gán (thay thế, thay thế): ZERO (ví dụ: nội dung của vị trí được thay thế bằng 0: L ← 0), SUCCESSOR (ví dụ: L ← L + 1) và DECREMENT (ví dụ: L ← L - 1). Rất ít khi lập trình viên phải viết 'mã' với một tập lệnh giới hạn như vậy. Nhưng Minsky chứng minh (như Melzak và Lambek) rằng cỗ máy của ông là Turing hoàn chỉnh chỉ với bốn loại lệnh chung: GOTO có điều kiện, GOTO vô điều kiện, gán / thay thế / thay thế và HALT. Tuy nhiên, một số hướng dẫn gán khác nhau (ví dụ: DECREMENT, INCREMENT và ZERO / CLEAR / EMPTY cho máy Minsky) cũng được yêu cầu để đạt tính chất Turing-completeness; đặc điểm kỹ thuật chính xác của chúng phần nào phụ thuộc vào nhà thiết kế. GOTO vô điều kiện là một sự tiện lợi; nó có thể được xây dựng bằng cách khởi tạo một vị trí chuyên dụng bằng 0, ví dụ như lệnh 'Z ← 0'; sau đó lệnh IF Z = 0 THEN GOTO xxx là vô điều kiện.
Mô phỏng thuật toán: ngôn ngữ máy tính (computor): Knuth khuyên đọc giả rằng 'cách tốt nhất để học một thuật toán là thử nó. Lấy giấy bút ra và làm việc với một ví dụ'. Nhưng những gì về một mô phỏng hoặc thực hiện các điều thực tế? Lập trình viên phải dịch thuật toán thành ngôn ngữ mà trình mô phỏng / máy tính / trình biên dịch có thể thực thi một cách hiệu quả. Stone cung cấp một ví dụ về điều này: khi tính toán căn bậc hai, người tính toán phải biết cách lấy căn bậc hai. Nếu không, thuật toán, để hiệu quả, phải cung cấp một bộ quy tắc để trích xuất căn bậc hai.
Điều này có nghĩa là lập trình viên phải biết một 'ngôn ngữ' hiệu quả đối với máy tính. Tuy nhiên, việc lựa chọn mô hình mô phỏng vẫn còn tùy ý. Van Emde Boas chú ý rằng 'dù ta xây dựng trên lý thuyết trừu tượng thay vì mô hình cụ thể, sự tùy tiện vẫn tồn tại. Điều này phát triển khái niệm mô phỏng'. Khi đánh giá tốc độ, tập lệnh là yếu tố quan trọng. Ví dụ, chương trình con trong thuật toán Euclid để tính phần dư sẽ nhanh hơn nếu lập trình viên có lệnh 'modulo' thay vì chỉ phép trừ (hoặc kém hơn: chỉ 'giảm dần' của Minsky).
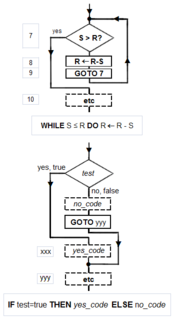
Lập trình có cấu trúc, cấu trúc chuẩn: Theo quan điểm của Church – Turing, mọi thuật toán đều có thể được tính toán bằng một mô hình Turing hoàn chỉnh. Theo Minsky, chỉ cần bốn loại lệnh — GOTO có điều kiện, GOTO không điều kiện, phép gán và HALT — là đủ để đảm bảo tính đầy đủ của Turing. Kemeny và Kurtz nhấn mạnh rằng, mặc dù sử dụng GOTO vô kỷ luật và IF-THEN GOTO có thể dẫn đến 'mã spaghetti', lập trình viên vẫn có thể viết các chương trình có cấu trúc chỉ với những hướng dẫn này. Tausworthe mở rộng ba cấu trúc cổ điển Böhm-Jacopini: SEQUENCE, IF-THEN-ELSE và WHILE-DO, cùng với DO-WHILE và CASE. Lợi ích của chương trình có cấu trúc là nó tự chứng minh tính đúng đắn bằng cách sử dụng quy nạp toán học.
Các biểu đồ hợp quy: Biểu đồ là phương tiện đồ họa mô tả và ghi lại một thuật toán (và chương trình máy tính thực hiện thuật toán đó). Giống như quy trình chương trình của máy Minsky, biểu đồ luôn bắt đầu từ đầu và diễn ra xuôi. Các ký hiệu chính gồm có bốn loại: mũi tên chỉ hướng luồng chương trình, hình chữ nhật (SEQUENCE, GOTO), hình thoi (IF-THEN-ELSE) và dấu chấm (OR-tie). Các cấu trúc cổ điển Böhm – Jacopini được xây dựng từ những hình ảnh cơ bản này. Cấu trúc con có thể 'lồng' trong hình chữ nhật, nhưng chỉ khi có một lối ra duy nhất từ cấu trúc cha. Cách sử dụng các ký hiệu này để xây dựng các cấu trúc chính tắc được minh họa trong biểu đồ.
Ví dụ
Ví dụ về thuật toán
Một trong những thuật toán đơn giản nhất là tìm số lớn nhất trong danh sách các số có thứ tự ngẫu nhiên. Cách giải yêu cầu kiểm tra từng số trong danh sách và đưa ra kết quả dựa trên số lớn nhất đã tìm thấy.
Mô tả cấp cao:
- Nếu không có số nào trong tập hợp thì không có số lớn nhất.
- Giả sử số đầu tiên trong tập hợp là số lớn nhất.
- Với mỗi số còn lại trong tập hợp: nếu số này lớn hơn số lớn nhất hiện tại thì coi số này là số lớn nhất.
- Khi không còn số nào trong tập hợp để xét, số lớn nhất hiện tại là số lớn nhất của tập hợp.
Bản mô tả chính thức: Viết bằng văn xuôi gần với ngôn ngữ cấp cao của chương trình máy tính hơn, đây là cách mã hóa chính thức hơn của thuật toán bằng mã giả hoặc ngôn ngữ giản lược:
Input: Danh sách các số L. Output: Số lớn nhất trong danh sách L.
nếu L.kích thước = 0 trả lại null lớn nhất ← L[0] cho mỗi mục trong L, làm nếu mục > lớn nhất, thì lớn nhất ← mục trả lại lớn nhất
Thuật toán Euclid
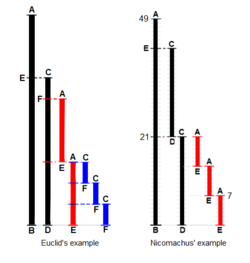
Thuật toán Euclid để tính ước số chung lớn nhất (ƯCLN) cho hai số, xuất hiện dưới dạng Mệnh đề II trong Quyển VII ('Lý thuyết số cơ bản') của công trình Cơ sở của ông. Do đó, Euclid đặt ra câu hỏi: 'Cho hai số không nguyên tố với nhau, hãy tìm ước số chung lớn nhất của chúng'. Ông định nghĩa rằng 'Một số [là] một tập hợp bao gồm các đơn vị': một số lượng, một số nguyên dương không bao gồm số không. Để 'đo' là đặt một chiều dài ngắn s lên một chiều dài dài l cho đến khi phần còn lại nhỏ hơn chiều dài ngắn s. Theo cách hiện đại, phần dư r = l - q × s, q là số nguyên thương, hoặc phần dư r là 'môđun', phần còn lại sau khi chia.
Để thuật toán Euclid thành công, điều kiện bắt đầu là độ dài phải thỏa mãn hai yêu cầu: (i) độ dài không được bằng 0, VÀ (ii) phép trừ phải là 'hợp lệ'; nghĩa là, một thử thách phải đảm bảo rằng số nhỏ hơn trong hai số mà chúng ta đang lấy đi số lớn hơn (hoặc hai số có thể bằng nhau để kết quả của phép trừ là 0).
Chứng minh ban đầu của Euclid bổ sung một yêu cầu thứ ba: hai độ dài không phải là nguyên tố với nhau. Euclid đã quy định điều này để có thể xây dựng một bằng chứng rút gọn là vô lý rằng số đo chung của hai số thực tế là lớn nhất. Trong khi thuật toán của Nicomachus cũng giống như của Euclid, khi hai số nguyên tố với nhau, nó mang lại số '1' cho số đo chung của chúng. Vì vậy, chính xác mà nói, đây là thuật toán của Nicomachus.

1599 = 650×2 + 299 650 = 299×2 + 52 299 = 52×5 + 39 52 = 39×1 + 13 39 = 13×3 + 0
Ngôn ngữ máy tính cho thuật toán Euclid
Chỉ một số loại lệnh được yêu cầu để thực thi thuật toán Euclid — một số phép thử logic (GOTO có điều kiện), GOTO không điều kiện, phép gán (thay thế) và phép trừ.
- Vị trí được ký hiệu bằng (các) chữ cái viết hoa, ví dụ: S, A, v.v.
- Số lượng (số) khác nhau ở một vị trí được viết bằng (các) chữ cái thường và (thường) được kết hợp với tên của vị trí. Ví dụ, vị trí L ở đầu có thể chứa số l = 3009.
Một chương trình đơn giản cho thuật toán Euclid
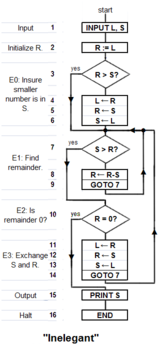
Thuật toán sau đây được viết bằng bốn bước theo Knuth của Euclid và Nicomachus, nhưng thay vì sử dụng phép chia để tìm phần dư, nó sử dụng các phép trừ liên tiếp của độ dài s từ độ dài còn lại r cho đến khi r nhỏ hơn s. Mô tả cấp cao, in đậm, phỏng theo Knuth 1973: 2–4:
ĐẦU VÀO:
1 [Vào hai vị trí L và S đặt các số l và s
2 [Khởi tạo R: làm cho độ dài còn lại r bằng với độ dài ban đầu/bắt đầu/nhập l]: R ← L
E0: [Đảm bảo r ≥ s. ]
3 [Đảm bảo số nhỏ hơn trong hai số được đặt trong S và số lớn hơn trong R]: NẾU R > S THEN nội dung của L là số lớn hơn nên bỏ qua các bước trao đổi 4, 5 và 6: GOTO bước 6 ELSE đổi chỗ nội dung của R và S.
4 L ← R (bước đầu tiên này là dư thừa, nhưng hữu ích cho cuộc thảo luận sau này).
5 R ← S
6 S ← L
E1: [Tìm phần dư]: Cho đến khi độ dài còn lại r trong R nhỏ hơn độ dài ngắn hơn s trong S, lặp đi lặp lại phép trừ số đo s trong S với độ dài còn lại r trong R.
7 NẾU S > R THEN đo xong nên GOTO 10 ELSE đo lại,
8 R ← R − S
9 [Vòng lặp phần dư]: GOTO 7.
E2: [Phần dư có bằng 0? ]: HOẶC (i) số đo cuối cùng là chính xác, phần còn lại trong R bằng 0 và chương trình có thể tạm dừng, HOẶC (ii) thuật toán phải tiếp tục: số đo cuối cùng để lại phần dư trong R nhỏ hơn số đo trong S.
10 NẾU R = 0 THÌ đã xong nên GOTO bước 15 ELSE TIẾP TỤC ĐẾN bước 11,
E3: [Đảo vị trí s và r ]: Điểm mấu chốt của thuật toán Euclid. Sử dụng phần dư r để đo số trước đó nhỏ hơn s; L phục vụ như một kho lưu trữ tạm thời.
11 L ← R
12 R ← S
13 S ← L
14 [Lặp lại quá trình đo đạc]: GOTO 7
ĐẦU RA:
15 [Hoàn tất. S chứa ước số chung lớn nhất]: IN S
XONG:
16 DỪNG, KẾT THÚC, DỪNG LẠI.
Một chương trình đơn giản cho thuật toán Euclid
Phiên bản sau của thuật toán Euclid chỉ cần sáu lệnh cốt lõi để thực hiện mười ba lệnh được yêu cầu bởi 'chương trình chưa thanh lịch'; khác với 'chương trình chưa thanh lịch' cần nhiều loại hướng dẫn hơn. [làm rõ] Bạn có thể tìm thấy sơ đồ của 'Thanh lịch' ở đầu bài viết này. Trong ngôn ngữ BASIC (không có cấu trúc), các bước được đánh số và lệnh LET [] = [] là lệnh gán được ký hiệu bằng ←.
5 REM Thuật toán Euclid cho ước số chung lớn nhất 6 IN 'Nhập hai số nguyên lớn hơn 0' 10 NHẬP A,B 20 NẾU B=0 THÌ ĐI TỚI 80 30 NẾU A > B THÌ ĐI TỚI 60 40 CHO B=B-A 50 ĐI TỚI 20 60 CHO A=A-B 70 ĐI TỚI 20 80 IN A 90 KẾT THÚC
Cách 'chương trình thanh lịch' hoạt động: Thay vì vòng lặp Euclid bên ngoài, 'Elegant' di chuyển giữa hai vòng lặp con, một vòng lặp A> B tính A ← A - B và một vòng lặp B ≤ A tính B ← B - A. Điều này hoạt động vì khi giá trị cuối cùng của Minuend M nhỏ hơn hoặc bằng S (chênh lệch = Minuend - Subtrahend), Minuend có thể trở thành s (chiều dài đo mới) và Subtrahend có thể trở thành r mới (độ dài được đo); nói cách khác, 'ý nghĩa' của phép trừ được đảo ngược. Phiên bản sau này có thể được sử dụng với các ngôn ngữ hướng đối tượng:
// Thuật toán Euclid cho ước số chung lớn nhất int euclidAlgorithm (int A, int B){ A=Math.abs(A); B=Math.abs(B); while (B!=0){ if (A>B) A=A-B; else B=B-A; } return A; }
Đánh giá các thuật toán Euclid
Một thuật toán có thực hiện những gì tác giả mong muốn không? Một số thử nghiệm thường cung cấp sự tin tưởng vào tính năng cốt lõi. Tuy nhiên, chỉ có thử nghiệm là không đủ. Đối với thử nghiệm, một nguồn sử dụng 3009 và 884. Knuth đề xuất 40902, 24140. Một trường hợp thú vị khác là hai số nguyên tố cùng nhau 14157 và 5950.
Nhưng các 'trường hợp ngoại lệ' phải được xác định và thử nghiệm. Liệu 'Chưa thanh lịch' có thực hiện đúng khi R> S, S> R, R = S không? Tương tự cho chương trình 'Thanh lịch': B> A, A> B, A = B? (Áp dụng cho tất cả). Điều gì sẽ xảy ra khi một số bằng 0, cả hai số đều bằng 0? ('Chưa thanh lịch' sẽ rơi vào vòng lặp vô hạn trong các trường hợp này; 'Thanh lịch' sẽ rơi vào vòng lặp vô hạn khi A = 0.) Những thất bại đáng chú ý như vụ nổ tên lửa Ariane 5 Flight 501 (ngày 4 tháng 6 năm 1996) là các ngoại lệ kiểu như vậy.
Chứng minh tính chính xác của chương trình bằng phương pháp quy nạp toán học: Knuth chứng minh việc áp dụng quy nạp toán học cho phiên bản 'mở rộng' của thuật toán Euclid và đề xuất 'một phương pháp áp dụng chung để chứng minh tính hợp lệ của bất kỳ thuật toán nào'. Tausworthe đề xuất rằng thước đo phức tạp của chương trình là độ dài của bằng chứng chính xác của nó.
Đánh giá và cải tiến thuật toán Euclid
Thanh lịch (tối ưu hóa) so với hiệu quả (tốc độ): Với chỉ sáu lệnh cốt lõi, 'Thanh lịch' rõ ràng chiến thắng so với 'Không thanh lịch' với 13 lệnh. Tuy nhiên, 'Không thanh lịch' nhanh hơn (đạt đến HALT trong ít bước hơn). Phân tích thuật toán chỉ ra lý do tại sao như vậy: 'Thanh lịch' thực hiện hai phép thử điều kiện trong mỗi vòng trừ, trong khi 'Không thanh lịch' chỉ thực hiện một phép thử. Vì thuật toán (thường) yêu cầu nhiều lần lặp lại, trung bình sẽ lãng phí nhiều thời gian để thực hiện 'B = 0?' kiểm tra chỉ cần thiết sau khi phần còn lại được tính toán.
Có thể cải thiện các thuật toán được không?: Khi lập trình viên đánh giá một chương trình là 'phù hợp' và 'hiệu quả' - nghĩa là nó tính toán chức năng mà tác giả dự định - thì câu hỏi sẽ là liệu nó có thể được cải thiện không?
Có thể cải thiện độ nhỏ gọn của 'Không thanh lịch' bằng cách loại bỏ năm bước. Nhưng Chaitin đã chứng minh rằng việc nén một thuật toán không thể tự động hóa bằng một thuật toán tổng quát; đúng hơn, nó chỉ có thể được thực hiện theo kinh nghiệm; tức là, bằng cách tìm kiếm đầy đủ, thử và sai, thông minh, sáng suốt, áp dụng suy luận quy nạp, v.v. Quan sát các bước 4, 5 và 6 được lặp lại trong các bước 11, 12 và 13. So sánh với 'Thanh lịch' cho thấy rằng các bước này, cùng với các bước 2 và 3, có thể bị loại bỏ. Điều này làm giảm số lượng lệnh cốt lõi từ 13 xuống 8, làm cho nó 'thanh lịch' hơn 'Không thanh lịch', với chín bước.
Tốc độ của 'Thanh lịch' có thể được cải thiện bằng cách di chuyển kiểm tra 'B = 0?' ra khỏi hai vòng trừ. Thay đổi này yêu cầu bổ sung ba lệnh (B = 0 ?, A = 0 ?, GOTO). Bây giờ 'Thanh lịch' tính toán các số ví dụ nhanh hơn; liệu điều này luôn đúng với bất kỳ A, B và R, S nào cho trước hay không sẽ yêu cầu một phân tích chi tiết.
Tìm hiểu thêm
- Độ phức tạp của các thuật toán
- Máy truy xuất dữ liệu
- Thuật toán sắp xếp
Những lĩnh vực chính của khoa học máy tính | |
|---|---|
| Các nền tảng toán học | Logic toán · Lý thuyết tập hợp · Lý thuyết số · Lý thuyết đồ thị · Lý thuyết kiểu · Lý thuyết thể loại · Giải tích số · Lý thuyết thông tin · Đại số · Nhận dạng mẫu · Nhận dạng tiếng nói · Toán học tổ hợp · Đại số Boole · Toán rời rạc |
| Lý thuyết phép tính | Độ phức tạp Kolmogorov · Lý thuyết Automat · Lý thuyết tính được · Lý thuyết độ phức tạp tính toán · Lý thuyết điện toán lượng tử |
| Các cấu trúc dữ liệu và các giải thuật | Phân tích giải thuật · Thiết kế giải thuật · Hình học tính toán · Tối ưu hóa tổ hợp |
| Các ngôn ngữ lập trình và Các trình biên dịch | Các bộ phân tích cú pháp · Các trình thông dịch · Lập trình cấu trúc · Lập trình thủ tục · Lập trình hướng đối tượng · Lập trình hướng khía cạnh · Lập trình hàm · Lập trình logic · Lập trình máy tính · Lập trình mệnh lệnh · Lập trình song song · Lập trình tương tranh · Các mô hình lập trình · Prolog · Tối ưu hóa trình biên dịch |
| Tính song hành, Song song, và các hệ thống phân tán | Đa xử lý · Điện toán lưới · Kiểm soát song hành · Hiệu năng hệ thống · Tính toán phân tán |
| Công nghệ phần mềm | Phân tích yêu cầu · Thiết kế phần mềm · Các phương pháp hình thức · Kiểm thử phần mềm · Quy trình phát triển phần mềm · Các phép đo phần mềm · Đặc tả chương trình · LISP · Mẫu thiết kế · Tối ưu hóa phần mềm |
| Kiến trúc hệ thống | Kiến trúc máy tính · Tổ chức máy tính · Các hệ điều hành · Các cấu trúc điều khiển · Cấu trúc bộ nhớ lưu trữ · Vi mạch · Thiết kế ASIC · Vi lập trình · Vào/ra dữ liệu · VLSI design · Xử lý tín hiệu số |
| Viễn thông và Mạng máy tính | Audio máy tính · Chọn tuyến · Cấu trúc liên kết mạng · Mật mã học |
| Các cơ sở dữ liệu và Các hệ thống thông tin | Hệ quản trị cơ sở dữ liệu · Cơ sở dữ liệu quan hệ · SQL · Các giao dịch · Các chỉ số cơ sở dữ liệu · Khai phá dữ liệu · Biểu diễn và giao diện thông tin · Các hệ thống thông tin · Khôi phục dữ liệu · Lưu trữ thông tin · Lý thuyết thông tin · Mã hóa dữ liệu · Nén dữ liệu · Thu thập thông tin |
| Trí tuệ nhân tạo | Lập luận tự động · Ngôn ngữ học tính toán · Thị giác máy tính · Tính toán tiến hóa · Các hệ chuyên gia · Học máy · Xử lý ngôn ngữ tự nhiên · Robot học |
| Đồ họa máy tính | Trực quan hóa · Hoạt họa máy tính · Xử lý ảnh |
| Giao diện người-máy tính | Khả năng truy cập máy tính · Giao diện người dùng · Điện toán mang được · Điện toán khắp mọi nơi · Thực tế ảo |
| Khoa học tính toán | Cuộc sống nhân tạo · Tin sinh học · Khoa học nhận thức · Hóa học tính toán · Khoa học thần kinh tính toán · Vật Lý học tính toán · Các giải thuật số · Toán học kí hiệu |
Chú ý: khoa học máy tính còn có thể được chia thành nhiều chủ đề hay nhiều lĩnh vực khác dựa theo Hệ thống xếp loại điện toán ACM. | |
