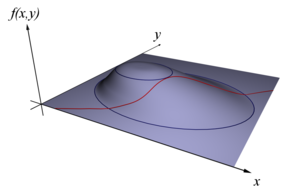
Trong lĩnh vực tối ưu hóa, phương pháp Lagrange nhân tử (đặt theo tên nhà toán học Joseph Louis Lagrange) là kỹ thuật dùng để tìm cực tiểu hoặc cực đại địa phương của hàm số có điều kiện ràng buộc.
Ví dụ (tham khảo Hình 1), hãy xem xét bài toán tối ưu hóa.
- Tìm giá trị cực đại của hàm f(x, y)
- với điều kiện ràng buộc g(x, y) = 0.
Cả f và g đều phải liên tục tại đạo hàm riêng bậc nhất của chúng. Đặt một biến mới (λ) gọi là nhân tử Lagrange và nghiên cứu hàm Lagrangian được định nghĩa bởi
Biến λ có thể cộng hoặc trừ. Nếu f(x0, y0) là giá trị cực đại của f(x, y) trong bài toán ban đầu, sẽ tồn tại λ0 sao cho (x0, y0, λ0) là một điểm dừng của hàm Lagrangian. Tuy nhiên, không phải mọi điểm dừng đều cho nghiệm của bài toán. Phương pháp này chỉ mang lại điều kiện cần cho tối ưu hóa. Điều kiện đủ cho cực tiểu và cực đại cũng cần phải thỏa mãn.
Tham khảo liên kết ngoài
Giới thiệu
- Giới thiệu khái niệm (cùng với một thảo luận ngắn về phương pháp Lagrange multipliers trong giải tích biến phân được ứng dụng trong vật lý)
- Lagrange Multipliers cho Các Hình Thức Bậc Hai Với Các Ràng Buộc Tuyến Tính của Kenneth H. Carpenter
Tham khảo thêm văn bản và các ứng dụng tương tác
- Giải thích đơn giản với ví dụ về cách chính phủ sử dụng thuế như phương pháp Lagrange multipliers
- Lagrange Multipliers không gây tổn thương lâu dài, giải thích tập trung vào trực giác của Dan Klein
- Biểu diễn hình học của phương pháp Lagrange Multipliers: Cung cấp cái nhìn sâu sắc về hai chiều, tại điểm cực tiểu, hướng dốc nhất phải vuông góc với tiếp tuyến của đường ràng buộc tại điểm đó. [Yêu cầu InternetExplorer/Firefox/Safari] Minh họa bằng Mathematica của Shashi Sathyanarayana
- Ứng dụng tương tác
- Bài giảng video về Lagrange Multipliers
- Bài giảng video từ MIT OpenCourseware về Lagrange Multipliers trong khóa học Giải tích đa biến
- Slides kèm theo sách giáo khoa tối ưu hóa phi tuyến của Bertsekas, với chi tiết về Lagrange multipliers (bài giảng 11 và 12)
- Ý tưởng hình học đằng sau phương pháp Lagrange multipliers
