Quay lui (tiếng Anh: backtracking) là một chiến lược tìm kiếm giải pháp cho các bài toán ràng buộc. Thuật ngữ này được nhà toán học người Mỹ D. H. Lehmer giới thiệu vào thập niên 1950.
Giải nghĩa
Bài toán thỏa mãn ràng buộc là những bài toán có một giải pháp hoàn chỉnh, trong đó thứ tự các phần tử không quan trọng. Bài toán bao gồm một tập biến và mỗi biến được gán giá trị dựa trên các ràng buộc cụ thể. Quay lui thử tất cả các tổ hợp để tìm giải pháp. Ưu điểm của phương pháp này là nhiều cài đặt có thể bỏ qua các tổ hợp không hoàn chỉnh, giúp giảm thời gian chạy.
Phương pháp quay lui có liên hệ mật thiết với tìm kiếm tổ hợp.
Triển khai
Bản chất của phương pháp là thử tất cả các khả năng cho đến khi tìm được lời giải đúng. Đây là quá trình tìm kiếm theo chiều sâu trong một tập hợp các phương án. Khi gặp một lựa chọn không thỏa mãn, ta quay lui về điểm trước đó để thử các lựa chọn khác. Nếu đã thử hết các phương án mà không thành công, ta quay lại điểm trước đó và tiếp tục thử. Quá trình thất bại khi không còn lựa chọn nào để quay lui.
Quá trình này thường được cài đặt bằng hàm đệ quy, mỗi lần gán một biến và thử tất cả các giá trị khả dĩ, sau đó gọi tiếp chuỗi đệ quy để xử lý các biến tiếp theo. Chiến lược quay lui giống với tìm kiếm theo chiều sâu nhưng tiết kiệm bộ nhớ hơn, chỉ lưu trạng thái lời giải hiện tại và cập nhật nó.
Để tối ưu hóa, khi chọn một giá trị, trước khi gọi hàm đệ quy, thuật toán thường loại giá trị đó khỏi miền xác định của các biến xung đột (kiểm tra tiến - forward checking) và kiểm tra ràng buộc để loại trừ các giá trị khác không hợp lệ (lan truyền ràng buộc - constraint propagation).
Chiến lược Heuristic
Người ta thường áp dụng các phương pháp heuristic để tăng tốc quá trình quay lui. Vì có thể xử lý các biến theo bất kỳ thứ tự nào, việc ưu tiên xử lý các biến có ít lựa chọn nhất thường giúp tỉa bớt cây tìm kiếm sớm hơn, tối đa hóa hiệu quả của lựa chọn hiện tại.
Các thuật toán quay lui phức tạp thường dùng một hàm biên để kiểm tra xem từ lời giải chưa hoàn chỉnh hiện tại có thể dẫn đến lời giải hoàn chỉnh không. Điều này giúp phát hiện sớm những hướng đi không khả thi, cải thiện hiệu quả tìm kiếm. Tuy nhiên, vì hàm biên được gọi nhiều lần nên cần đảm bảo chi phí tính toán của nó ở mức tối thiểu, nếu không sẽ ảnh hưởng đến hiệu quả tổng thể. Các hàm kiểm tra biên thường dựa trên việc nới lỏng một số điều kiện của bài toán, giống như các hàm heuristic khác.
Minh họa
Chiến lược quay lui có thể được dùng để giải các bài toán liệt kê cấu hình. Mỗi cấu hình được xây dựng dần dần, với mỗi phần tử được chọn bằng cách thử tất cả các phương án có thể.
Cách tiếp cận
Cấu hình cần liệt kê có dạng (x₁, x₂, ..., xₙ). Thuật toán quay lui được thực hiện qua các bước sau:
- 1) Xét tất cả các giá trị có thể của x₁ và thử lần lượt các giá trị đó. Với mỗi giá trị thử cho x₁, thực hiện tiếp:
- 2) Xét tất cả các giá trị có thể của x₂ và thử lần lượt các giá trị đó. Với mỗi giá trị thử cho x₂, lại tiếp tục xét khả năng của x₃... cho đến khi:
- n) Xét tất cả các giá trị có thể của xₙ, thử lần lượt các giá trị đó và khi tìm được cấu hình (x₁, x₂, ..., xₙ), thông báo cấu hình này.
Diễn giải
Thuật toán quay lui có thể được diễn giải bằng mã giả (pseudocode) như sau:
{Thủ tục này sẽ thử cho x₁, x₂, ..., xᵢ nhận lần lượt các giá trị có thể}
procedure Thu(i: Integer);
begin
for mỗi giá trị khả dĩ của xᵢ do
begin
if (xᵢ là phần tử cuối trong cấu hình) then
else
begin
Try(i + 1); {Gọi đệ quy để tiếp tục chọn xᵢ₊₁}
end;
end;
end;
(Thuật toán quay lui bắt đầu với lời gọi Try(1);)
Quá trình tìm kiếm lời giải bằng thuật toán quay lui có thể minh họa qua cây sau:
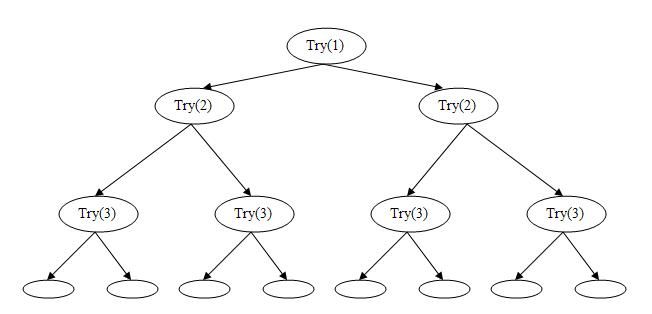
Tiếng Anh:
- CIS 680: Cấu trúc dữ liệu - Thuật toán quay lui Lưu trữ 2007-03-17 tại Wayback Machine
