1. Hướng dẫn giải bài toán xác định hai số khi biết hiệu và tỷ lệ giữa chúng
Để giải quyết bài toán tìm hai số khi đã biết hiệu và tỷ lệ giữa chúng, bạn có thể thực hiện theo các bước sau:
Bước 1: Vẽ sơ đồ các dữ kiện của bài toán. Trước khi bắt tay vào giải bài, việc vẽ sơ đồ các dữ kiện sẽ giúp bạn làm rõ thông tin đã cho và những gì cần tìm. Sơ đồ này sẽ giúp bạn hình dung rõ ràng hơn về mối quan hệ giữa các yếu tố trong bài toán.
Bước 2: Xác định số phần tương ứng với hiệu. Dựa trên thông tin đã có, chúng ta biết hiệu của hai số và tỷ lệ giữa chúng. Để tính số phần tương ứng với hiệu, ta cần chia hiệu của hai số cho tỷ lệ đã cho. Kết quả sẽ giúp chúng ta hiểu sự khác biệt giữa hai số và mức phân chia của chúng.
Bước 3: Tính số nhỏ và số lớn theo công thức.
- Trước hết, ta cần tính số nhỏ. Áp dụng công thức sau: Số nhỏ = (Hiệu hai số : số phần tương ứng) x số phần của số nhỏ. Công thức này giúp xác định giá trị của số nhỏ.
- Sau đó, tính số lớn theo công thức: Số lớn = (Hiệu hai số : tổng số phần tương ứng) x số phần của số lớn. Công thức này cho phép xác định giá trị của số lớn.
Bước 4: Xác định kết quả của bài toán. Sau khi thực hiện các phép tính theo công thức ở bước 3, ta sẽ có giá trị của số nhỏ và số lớn. Kết quả bài toán chính là hai số này.
Khi giải quyết bài toán, việc kiểm tra các điều kiện đặc biệt là rất quan trọng. Chẳng hạn như cần xem xét trường hợp tỉ số bằng 0 hoặc hiệu số các phần bằng nhau là 0. Trong những tình huống đặc biệt này, chúng ta cần xem xét lại phương pháp giải và có thể sẽ không tìm được đáp án chính xác.
2. Các loại bài tập liên quan đến hiệu và tỉ số
2.1. Loại bài toán cơ bản về hiệu và tỉ số
Bài toán cơ bản về hiệu và tỉ số yêu cầu chúng ta tìm hai số dựa trên thông tin về hiệu và tỉ lệ của chúng. Dưới đây là các bước chi tiết để giải loại bài toán này:
Bước 1: Xác định hiệu của hai số (nếu hiệu chưa được biết)
Khi đề bài không cung cấp hiệu của hai số, chúng ta cần xác định hiệu bằng cách lấy số lớn trừ đi số nhỏ.
Bước 2: Xác định tỉ số (nếu tỉ số chưa rõ)
Nếu đề bài không đưa ra tỉ số của hai số, chúng ta phải tính tỉ số bằng cách chia số lớn cho số nhỏ.
Bước 3: Vẽ sơ đồ
Tạo một sơ đồ với hai ô trống để biểu thị hai số cần tìm.
Bước 4: Xác định hiệu số phần bằng nhau
Tính hiệu số phần bằng nhau bằng cách trừ hai số trong tỉ số. Ví dụ: với tỉ số 8/5, hiệu số phần bằng nhau là 8 - 5 = 3.
Bước 5: Xác định số nhỏ
Số nhỏ được tính bằng cách lấy hiệu hai số và nhân với tỉ số phần của số nhỏ. Ví dụ: nếu hiệu là 36 và tỉ số phần của số nhỏ là 5, số nhỏ sẽ là (36/3) x 5.
Bước 6: Tính số lớn
Để tính số lớn, ta cộng số nhỏ với hiệu. Ví dụ, nếu số nhỏ là 60 và hiệu là 36, số lớn sẽ là 60 + 36.
Hiệu giữa hai số là 36 và tỉ số của chúng là 8/5. Hãy xác định hai số đó.

Dựa vào sơ đồ:
- Hiệu số phần bằng nhau được tính là 8 - 5 = 3 (phần)
- Số nhỏ là: (36/3) x 5 = 60
- Số lớn là: 60 + 36 = 96
Kết quả: Số nhỏ là 60, số lớn là 96.
Các tình huống đặc biệt: Trong một số trường hợp, đề bài có thể thiếu thông tin về hiệu hoặc tỉ số, hoặc yêu cầu thêm dữ kiện để xác định số cần tìm. Trong những trường hợp này, cần thực hiện thêm các phép tính và bổ sung thông tin để xác định hiệu hoặc tỉ số mới nhằm giải bài toán.
2.2. Loại bài toán hiệu - tỉ (ẩn số)
Để giải quyết dạng bài toán ẩn tỉ số, bạn có thể thực hiện các bước sau:
Ví dụ: Có hai thùng dầu, thùng thứ nhất chứa ít hơn thùng thứ hai 24 lít. Biết rằng 5 lần số dầu trong thùng thứ nhất bằng 3 lần số dầu trong thùng thứ hai. Tìm lượng dầu trong mỗi thùng.
Hướng dẫn giải:
Bước 1: Xác định tỉ số giữa lượng dầu trong hai thùng.
Dựa vào đề bài, 5 lần lượng dầu trong thùng thứ nhất bằng 3 lần lượng dầu trong thùng thứ hai. Từ đó, ta có tỉ số giữa hai thùng là:
Tỉ số = 5/3
Bước 2: Xác định số lít dầu trong từng thùng dựa trên bài toán hiệu và tỉ số.
Để giải quyết bài toán, chúng ta sử dụng thông tin về hiệu và tỉ số. Hiệu số là 24 lít (thùng thứ nhất kém thùng thứ hai 24 lít). Từ đó, chúng ta có:
Lượng dầu trong thùng thứ nhất = (Hiệu số : Tỉ số + 1) x 5 = (24 : (5/3) + 1) x 5
Lượng dầu trong thùng thứ hai = Lượng dầu trong thùng thứ nhất + Hiệu số = [(24 : (5/3) + 1) x 5] + 24
Bước 3: Tổng kết kết quả bài toán.
Sau khi thực hiện các phép tính, chúng ta có số lít dầu trong từng thùng. Đáp án của bài toán là:
Thùng thứ nhất: [24 : (5/3) + 1] x 5 lít dầu. Thùng thứ hai: [(24 : (5/3) + 1) x 5] + 24 lít dầu
Khi giải bài toán, cần lưu ý kiểm tra các điều kiện đặc biệt, chẳng hạn như trường hợp tỉ số bằng 0 hoặc tỉ số âm. Nếu gặp các tình huống này, cần xem xét lại phương pháp giải và có thể không đạt được đáp án chính xác.
2.3. Loại bài toán hiệu (ẩn) - tỉ số
Bài toán ẩn hiệu là dạng bài toán trong đó hiệu giữa hai số không được cung cấp, nhưng tỉ số của chúng đã được biết.
Ví dụ: Một hình chữ nhật có chiều dài bằng 3/2 chiều rộng. Nếu tăng chiều rộng thêm 10m, hình chữ nhật sẽ trở thành hình vuông. Tính diện tích của hình chữ nhật.
Để giải bài toán này, ta cần thực hiện các bước sau đây:
Bước 1: Xác định hiệu giữa chiều dài và chiều rộng
Trước hết, ta biết rằng khi tăng chiều rộng thêm 10m, hình chữ nhật sẽ trở thành hình vuông, tức là chiều dài sẽ bằng chiều rộng. Do đó, hiệu giữa chiều dài và chiều rộng là 10m.
Bước 2: Xác định chiều dài và chiều rộng của hình chữ nhật dựa trên dạng toán hiệu tỉ số
- Áp dụng dạng toán hiệu tỉ số, ta tính hiệu số phần bằng nhau, là hiệu giữa tử số và mẫu số của tỉ số. Ví dụ: với tỉ số 3/2, hiệu số phần bằng nhau là 3 - 2 = 1.
- Tiếp theo, ta tính chiều dài bằng cách nhân hiệu với chiều rộng. Ví dụ: nếu hiệu là 10 và chiều rộng là 2, chiều dài sẽ là (10/1) x 2.
Bước 3: Tính diện tích của hình chữ nhật
- Để tính diện tích của hình chữ nhật, ta lấy chiều dài nhân với chiều rộng.
Bước 4: Kết luận bài toán
- Trình bày kết quả cuối cùng, đó chính là diện tích của hình chữ nhật.
Bài giải:
Sơ đồ minh họa:
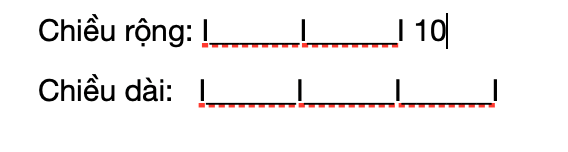
Tìm hai số dựa trên hiệu và tỷ số của chúng, dành cho học sinh lớp 4
Hiệu của các phần bằng nhau là 3 - 2 = 1 (phần)
Chiều dài của hình chữ nhật được tính là: (10/1) x 3 = 30 (m)
Chiều rộng của hình chữ nhật là: 30 - 10 = 20 (m)
Diện tích hình chữ nhật là: 20 x 30 = 600 (m2)
Kết quả: Diện tích hình chữ nhật là 600m²
2.4. Bài toán dạng hiệu - tỉ đều là ẩn số
Bài toán có hiệu và tỉ số chưa biết là loại bài toán trong đó cả hiệu và tỉ số của hai số đều chưa được biết. Để giải quyết, cần thực hiện các bước sau:
Bước 1: Xác định hiệu và tỉ số giữa tuổi của Lan và chị Lan
Biết tuổi hiện tại của Lan và chị Lan, chúng ta có thể tính hiệu giữa hai độ tuổi này.
Bước 2: Xác định tuổi của Lan và chị Lan dựa vào bài toán hiệu và tỉ số
- Áp dụng bài toán hiệu và tỉ số, ta tính hiệu số phần bằng nhau, tức là hiệu giữa tử số và mẫu số của tỉ số.
- Tiếp theo, ta tính tuổi của Lan dựa trên số phần bằng nhau và tuổi hiện tại của chị Lan.
Bước 3: Đưa ra kết luận bài toán
Trình bày kết quả, tức là số năm cần tìm để rac{1}{3} tuổi của Lan bằng rac{1}{7} tuổi của chị Lan.
Ví dụ: Hiện tại, Lan 8 tuổi và chị Lan 20 tuổi. Cần tính số năm nữa để rac{1}{3} tuổi của Lan bằng rac{1}{7} tuổi của chị Lan?
Bài giải:
- Hiệu tuổi giữa Lan và chị Lan là 20 - 8 = 12 (tuổi).
- Tỉ số giữa tuổi của Lan và chị Lan được tính là: 1/7 chia cho 1/3 = 3/7
Sơ đồ minh họa:
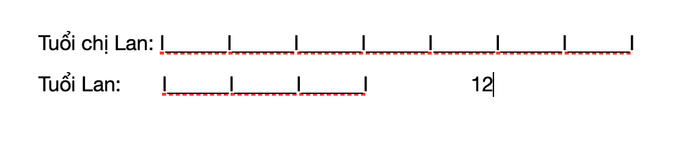
Tìm hai số khi biết hiệu và tỉ số của chúng, dành cho lớp 4.
Hiệu của các phần bằng nhau là 7 trừ 3, bằng 4 phần.
Tuổi của Lan trong tương lai sẽ là 12 chia cho 4 nhân với 3, tức là 9 tuổi.
Số năm cần tìm là 9 trừ 8, bằng 1 năm.
Kết quả: Sau 1 năm
