Phương pháp xác định góc giữa hai đường thẳng dễ hiểu và hiệu quả

1. Khái niệm về góc giữa hai đường thẳng

Góc giữa hai đường thẳng không chỉ quan trọng trong hình học và toán học mà còn xuất hiện trong nhiều tình huống thực tế. Ký hiệu α (alpha) dùng để biểu thị góc này, cho biết góc mà hai đường thẳng d và d' tạo ra khi chúng giao nhau. Góc này rất quan trọng trong việc đo lường và mô tả sự giao nhau và tương tác của các đối tượng trong không gian.

Góc α luôn nằm trong khoảng từ 0 đến 90 độ, tức là luôn dương và không vượt quá 90 độ. Đây là quy tắc cơ bản của góc trong không gian, ảnh hưởng đến cách chúng ta đo lường và hiểu về chúng. Góc giữa hai đường thẳng rất quan trọng trong việc xác định mối quan hệ và tương tác giữa các yếu tố hình học.

Tuy nhiên, có một trường hợp đặc biệt quan trọng: khi hai đường thẳng d và d' là song song hoặc trùng nhau. Trong tình huống này, không có điểm giao nhau ngoài góc giữa chúng, vì vậy góc giữa hai đường thẳng này bằng 0 độ.

Một phương pháp để xác định góc giữa hai đường thẳng là tính góc giữa hai vector chỉ phương của chúng. Nếu hai đường thẳng này được biểu diễn bằng hai vector chỉ phương a và b, thì cosin của góc giữa chúng có thể được tính bằng công thức sau:

Trong công thức trên, a · b là tích vô hướng của hai vector, |a| là độ dài của vector a, và |b| là độ dài của vector b.

Một phương pháp khác để tính góc giữa hai đường thẳng là dựa trên góc giữa hai vector pháp tuyến của chúng. Nếu n1 và n2 là hai vector pháp tuyến của d và d', thì cosin của góc giữa chúng có thể tính bằng công thức tương tự như trên:

Chẳng hạn, khi hai đường thẳng song song, các vector pháp tuyến của chúng cũng song song và cosin của góc giữa chúng sẽ là 1, tức là góc giữa hai đường thẳng là 0 độ, như đã đề cập ở trường hợp đặc biệt.

2. Phương pháp xác định góc giữa hai đường thẳng đơn giản và hiệu quả

Công thức để tính góc giữa hai đường thẳng

Để đo góc giữa hai đường thẳng a và b một cách chính xác, thường bắt đầu bằng việc chọn một điểm O thuộc một trong hai đường thẳng đó. Điều này giúp xác định điểm gốc cho tính toán và rõ ràng hai đường thẳng cắt nhau tại điểm này. Đây là điểm khởi đầu để xác định góc giữa hai đường thẳng, làm cho việc đo lường trở nên dễ hiểu và trực quan hơn.

Sau đó, chúng ta vẽ một đường thẳng qua điểm O với độ dốc hoặc hướng tương tự như hai đường thẳng a và b. Điều này cho phép chúng ta tạo ra hai vector chỉ phương, một cho đường thẳng a (gọi là vector u) và một cho đường thẳng b (gọi là vector v).

Khi biểu diễn vector u là vector chỉ phương của đường thẳng a và vector v là vector chỉ phương của đường thẳng b, chúng ta có thể sử dụng tích vô hướng của hai vector này để tính góc giữa hai đường thẳng a và b. Góc này ký hiệu là α (alpha) và có thể tính bằng công thức sau:

Trong công thức trên, (u, v) là tích vô hướng của hai vector u và v, |u| là độ dài của vector u, và |v| là độ dài của vector v. Sau khi tính được cosin của góc α, chúng ta có thể sử dụng hàm nghịch cosin để tính góc α chính xác.

Như vậy, bằng cách sử dụng vector chỉ phương và tích vô hướng của chúng, chúng ta có thể xác định góc giữa hai đường thẳng a và b một cách chính xác và hiệu quả.

Công thức

Xem xét vector n(x;y) và vector n'(x’;y’) là các vector pháp tuyến của hai đường thẳng d và d’. Góc giữa hai đường thẳng α được tính như sau:

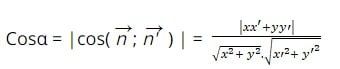
Phương pháp khác: Gọi k1 và k2 là các hệ số góc của hai đường thẳng d và d’. Góc giữa hai đường thẳng α có thể tính bằng công thức sau:

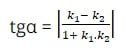
Ví dụ: Cho hai đường thẳng (a): x = -1 + mt; y = 9 + t, và (b): x + my - 4 = 0. Hãy xác định số giá trị của m sao cho góc giữa hai đường thẳng này là 60 độ.

A. 1 B. 2 C. 3 D. 4

Giải đáp

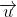
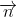
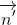
+ Để góc giữa hai đường thẳng trên bằng 60 độ thì:

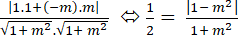
⇔ 1 + m^2 = 2.|1 - m^2| ()

+ Nếu -1 < m < 1 thì 1 - m^2 > 0. Từ () suy ra: 1 + m^2 = 2 (1 - m^2)

⇔ 1 + m^2 = 2 - 2m^2 ⇔ 3m^2 = 1

⇔ m^2 = 1/3 ⇔ m = ±1/√3 (điều kiện thỏa mãn).

+ Nếu m ≥ 1 hoặc m ≤ -1 thì 1 - m^2 ≤ 0. Từ (*) suy ra:

1 + m^2 = 2(m^2 - 1) ⇔ 1 + m^2 = 2m^2 - 2

⇔ m^2 = 3 ⇔ m = ±√3.

Có bốn giá trị của m thỏa mãn điều kiện này.

3. Phương pháp xác định giá trị góc

Có nhiều cách để xác định giá trị của góc tùy thuộc vào loại hình học cụ thể mà bạn đang sử dụng. Việc lựa chọn phương pháp phù hợp có thể dựa vào thông tin và công cụ có sẵn. Dưới đây là một số cách phổ biến để xác định giá trị góc:

- Sử dụng các đặc điểm hình học: Xác định giá trị góc có thể đơn giản hơn nếu bạn áp dụng các đặc điểm hình học của các hình cơ bản như hình vuông, hình chữ nhật hoặc tam giác.

Đối với hình vuông, bạn có thể chắc chắn rằng tất cả các góc đều bằng 90 độ. Đây là đặc điểm cơ bản của hình vuông, không cần phải đo đạc hay tính toán thêm.

Hình chữ nhật, một dạng hình học quen thuộc, có những đặc điểm riêng biệt. Các góc đối diện trong hình chữ nhật đều bằng nhau và đều có giá trị 90 độ. Điều này giúp bạn dễ dàng xác định giá trị góc mà không cần đến dụng cụ đo đạc.

Với tam giác, quy tắc cơ bản là tổng của ba góc luôn bằng 180 độ. Khi bạn biết giá trị của hai góc, bạn có thể dễ dàng tính góc còn lại bằng cách lấy 180 độ trừ đi tổng của hai góc đã biết.

Nhờ vào các đặc điểm hình học này, việc xác định giá trị góc trong các hình cơ bản trở nên nhanh chóng và hiệu quả, giúp bạn giải quyết bài toán hình học một cách dễ dàng hơn.

- Sử dụng thước đo góc hoặc êke: Để đo góc chính xác, bạn có thể dùng thước đo góc hoặc êke. Những công cụ này được thiết kế đặc biệt để đo góc với độ chính xác cao, giúp bạn xác định giá trị góc một cách dễ dàng.

Thước đo góc, thường có hình dạng giống chiếc quạt hoặc nửa hình tròn, là công cụ hữu ích để đo góc. Thước đo có thang đo từ 0 đến 180 độ, cho phép bạn đo góc giữa hai đoạn thẳng. Đặt thước đo hoặc êke chính xác vào hai đoạn thẳng, bạn có thể đọc giá trị góc trực tiếp trên thước đo.

Các công cụ đo góc rất đa dụng, phù hợp với nhiều ứng dụng từ xây dựng, thiết kế đến giải quyết các bài toán hình học. Nhờ vào độ chính xác cao, chúng cung cấp kết quả đo đạc tin cậy và giảm thiểu sai số, làm tăng hiệu quả công việc và đảm bảo tính chính xác trong các lĩnh vực hình học và khoa học.

Công cụ đo góc không chỉ mang lại độ chính xác và tin cậy mà còn giúp bạn giải quyết các bài toán hình học và khoa học một cách dễ dàng. Sử dụng thước đo góc hay êke là một phương pháp thông minh để đảm bảo kết quả đo đạc chính xác trong các ứng dụng khác nhau.

Tùy vào hoàn cảnh và dữ liệu hiện có, bạn có thể chọn phương pháp xác định góc phù hợp nhất để giải quyết vấn đề hình học của mình.