1. Các kiến thức cần ôn lại
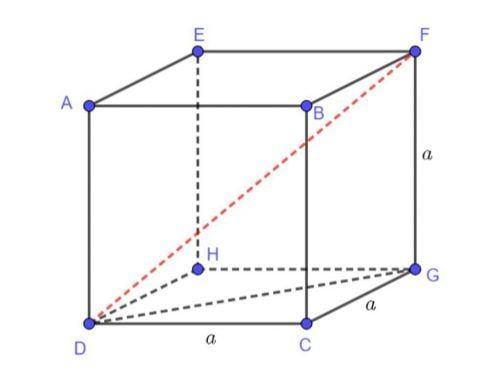
1.1. Hình hộp chữ nhật
Khái niệm: Hình hộp chữ nhật là một loại hình khối không gian với 6 mặt đều là hình chữ nhật, có 8 đỉnh và 12 cạnh. Các mặt đối diện của hình hộp song song với nhau. Vì vậy, hình hộp chữ nhật có 6 mặt được chia thành 3 cặp mặt đối diện, gồm 1 cặp mặt đáy và 2 cặp mặt bên.
Hai mặt đối diện của hình hộp chữ nhật được coi là hai mặt đáy, trong khi các mặt còn lại là các mặt bên của hình hộp.

Các công thức liên quan đến hình hộp chữ nhật:
Hình hộp chữ nhật được mô tả như sau:
(1).png)
.png)
Công thức 1: Tính diện tích xung quanh của hình hộp chữ nhật
Diện tích xung quanh của hình hộp chữ nhật được tính bằng cách nhân chu vi của đáy với chiều cao.
Sxq = 2h x (a + b)
Trong đó: Sxq là diện tích xung quanh của hình hộp chữ nhật;
h là chiều cao của hình hộp chữ nhật;
a và b lần lượt là chiều dài và chiều rộng của hình hộp chữ nhật.
Công thức 2: Tính diện tích toàn phần của hình hộp chữ nhật
Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích của 6 mặt của nó.
- Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích của tất cả 6 mặt.
- Diện tích toàn phần cũng bằng diện tích xung quanh cộng với diện tích của 2 mặt đáy còn lại.
Công thức: Stp = Sxq + 2ab
Diện tích toàn phần của hình hộp chữ nhật ký hiệu là Stp. Diện tích xung quanh ký hiệu là Sxq. Kích thước a và b lần lượt là chiều rộng và chiều dài của hình hộp chữ nhật.
Công thức 3: Cách tính thể tích của hình hộp chữ nhật
Để tính thể tích của hình hộp chữ nhật, ta nhân chiều cao với diện tích mặt đáy của nó.
Công thức: V = h x ab
V là thể tích của hình hộp chữ nhật. h là chiều cao của hình hộp chữ nhật. a và b là chiều dài và chiều rộng của hình hộp chữ nhật.
Công thức 4: Cách tính chiều cao của hình hộp chữ nhật
Dựa trên công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật, ta có thể suy ra công thức tính chiều cao như sau:
Công thức: h = Sxq / P = V / Sđáy
Trong đó: h là chiều cao của hình hộp chữ nhật. Sxq là diện tích xung quanh. P là chu vi mặt đáy, tính bằng P = (a + b) x 2. V là thể tích của hình hộp chữ nhật. Sđáy là diện tích đáy, tính bằng Sđáy = ab.
1.2. Hình lập phương
Khái niệm: Hình lập phương là khối hình có 6 mặt, 8 đỉnh và 12 cạnh, tất cả các mặt đều là hình vuông và các cạnh đều có độ dài bằng nhau. Nói cách khác, hình lập phương là khối có chiều rộng, chiều dài và chiều cao đều giống nhau.
Tính chất của hình lập phương:
- Tất cả 6 mặt đều giống nhau
- Có 12 cạnh có độ dài bằng nhau
- Các đường chéo của tất cả các mặt đều đồng dạng
- Các đường chéo không gian đều bằng nhau
Các công thức liên quan đến hình lập phương:
Công thức 1: Cách tính thể tích của hình lập phương: V = a³
Trong đó: V là thể tích của hình lập phương
a là chiều dài của mỗi cạnh hình lập phương
Công thức 2: Cách tính diện tích toàn phần của hình lập phương: Stp = 6 x a²
Trong đó: Stp là diện tích toàn phần của hình lập phương
a là chiều dài của mỗi cạnh hình lập phương
2. Các bài tập ôn tập
Bài 1: Một hình hộp chữ nhật có chiều dài 50 cm, chiều rộng 20 cm và diện tích xung quanh là 4900 cm². Hãy tính chiều cao của hình hộp chữ nhật đó.
Giải:
Chu vi đáy của hình hộp chữ nhật là: P = (a + b) x 2 = (50 + 20) x 2 = 140 cm
Chiều cao của hình hộp chữ nhật được tính bằng: h = Sxq / P = 4900 / 140 = 35 cm
Kết quả: 35 cm
Bài 2: Tính diện tích xung quanh của một hình hộp chữ nhật với diện tích xung quanh là 420 cm² và chiều cao là 10 cm. Tìm chu vi đáy của hình hộp chữ nhật đó.
Giải:
Diện tích xung quanh của hình hộp chữ nhật bằng chu vi đáy nhân với chiều cao, vì vậy ta có:
Chu vi đáy của hình hộp chữ nhật là: P = Sxq / h = 420 / 10 = 42 cm
Bài 3: Một phòng học hình hộp chữ nhật có các kích thước: Chiều dài 7,8 m, chiều rộng 6,2 m và chiều cao 4,3 m. Để sơn tường và trần của phòng này, cần trừ diện tích cửa ra là 8,1 m². Tính diện tích cần sơn của căn phòng.
Giải:
Diện tích xung quanh của phòng học tính cả diện tích của cửa chính, và nó chính là diện tích xung quanh của hình hộp chữ nhật.
Diện tích cần sơn của phòng học được tính bằng diện tích xung quanh cộng với diện tích của một đáy (trần nhà), sau đó trừ đi diện tích tổng các cửa.
Diện tích xung quanh của phòng học là: 2 x 4,3 x (7,8 + 6,2) = 120,4 m²
Diện tích cần sơn của phòng học là: (120,4 + 48,36) - 8,1 = 160,66 m²
Bài 4: Tính diện tích xung quanh và diện tích toàn phần của hình lập phương có cạnh dài 15 cm
Giải:
Diện tích xung quanh của hình lập phương là: (15 x 15) x 4 = 900 cm²
Diện tích toàn phần của hình lập phương là: (15 x 15) x 6 = 1350 cm²
Kết quả: 900 cm²; 1350 cm²
Bài 5: Một khối kim loại hình lập phương có cạnh dài 0,75 m. Mỗi decimet khối kim loại nặng 15 kg. Tính trọng lượng của khối kim loại đó.
Giải:
Thể tích của khối kim loại là: 0,75 x 0,75 x 0,75 = 0,421875 m³
Chuyển đổi: 0,421875 m³ = 421,875 dm³
Khối kim loại đó nặng: 15 x 421,875 = 6328,125 kg
Kết quả: 6328,125 kg
3. Đáp án chi tiết bài 116: Luyện tập chung Toán lớp 5
Bài 1: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật với các kích thước:
a) Chiều dài 0,9 m; chiều rộng 0,6 m; chiều cao 1,1 m
b) Chiều dài 4/5 dm; chiều rộng 2/3 dm; chiều cao 3/4 dm
Phương pháp giải: Sử dụng các công thức sau:
- Chu vi mặt đáy = (chiều dài + chiều rộng) x 2
- Diện tích xung quanh = chu vi mặt đáy x chiều cao
- Thể tích = chiều dài x chiều rộng x chiều cao
Giải chi tiết:
a) Chu vi mặt đáy của hình hộp chữ nhật là: (0,9 + 0,6) x 2 = 3 m
Diện tích xung quanh của hình hộp chữ nhật là: 3 x 1,1 = 3,3 m²
Thể tích của hình hộp chữ nhật là: 0,9 x 0,6 x 1,1 = 0,594 m³
b) Chu vi mặt đáy của hình hộp chữ nhật là: (4/5 + 2/3) x 2 = 44/15 dm
Diện tích xung quanh của hình hộp chữ nhật là: 44/15 x 3/4 = 132/60 = 11/5 dm²
Thể tích của hình hộp chữ nhật là: 4/5 x 2/3 x 3/4 = 2/5 dm³
Kết quả: a) Diện tích xung quanh 3,3 m²; thể tích 0,594 m³
b) Diện tích xung quanh 11/5 dm²; thể tích 2/5 dm³
Bài 2: Một hình lập phương có cạnh dài 3,5 dm. Tính diện tích toàn phần và thể tích của hình lập phương này.
Phương pháp giải: Sử dụng các công thức sau:
- Diện tích toàn phần = diện tích một mặt x 6 = cạnh x cạnh x 6
- Thể tích = cạnh x cạnh x cạnh
Lời giải chi tiết:
Diện tích toàn phần của hình lập phương là: 3,5 x 3,5 x 6 = 73,5 dm²
Thể tích của hình lập phương là: 3,5 x 3,5 x 3,5 = 42,875 dm³
Kết quả: Diện tích toàn phần 73,5 dm²; Thể tích 42,875 dm³
Bài 3: Với thể tích của hình lập phương là 27 cm³, hãy tính diện tích toàn phần của nó.
Hướng dẫn: Bạn có thể xác định độ dài cạnh của hình lập phương bằng cách thử với các giá trị như 1 cm, 2 cm, v.v.
Phương pháp giải:
Hình lập phương với độ dài cạnh là a có thể tích được tính bằng công thức V = a x a x a
Diện tích toàn phần được tính bằng diện tích của một mặt nhân với 6, tức là cạnh x cạnh x cạnh x 6
Giải thích chi tiết:
Nếu cạnh của hình lập phương là 3 cm, thì thể tích của nó sẽ là; 3 x 3 x 3 = 27 cm³
Vì vậy, hình lập phương có cạnh dài 3 cm
Diện tích toàn phần của hình lập phương là: (3 x 3) x 6 = 54 cm2
Kết quả là: 54 cm2
Bài 4: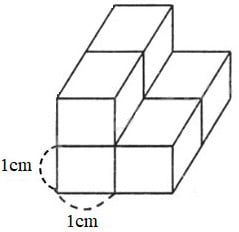
Hướng dẫn giải:
- Xác định thể tích của khối gỗ hình lập phương có cạnh 1cm
- Tính tổng số khối gỗ hình lập phương cạnh 1cm có trong khối gỗ đó
- Thể tích khối gỗ = thể tích của khối gỗ hình lập phương cạnh 1cm nhân với tổng số khối gỗ hình lập phương cạnh 1cm
Hướng dẫn giải chi tiết:
Thể tích của khối gỗ hình lập phương cạnh 1cm là: 1 x 1 x 1 = 1cm3
Nhìn vào hình vẽ, chúng ta thấy khối gỗ bao gồm 6 khối nhỏ hình lập phương có cạnh 1cm
Thể tích của khối gỗ là: 1 x 6 = 6 cm3
Kết quả là: 6 cm3
