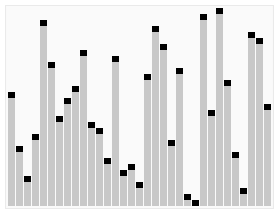
| Quicksort thực hiện trên danh sách các số. Đường nằm ngang là các giá trị làm phần tử chốt. | |
| Phân loại | Giải thuật sắp xếp |
|---|---|
| Cấu trúc dữ liệu | Khác nhau |
| Hiệu suất trường hợp tệ nhất | Trung bình Xấu nhất |
| Độ phức tạp không gian trường hợp tệ nhất | Khác nhau tùy vào cách hiện thực |
| Tối ưu | Thỉnh thoảng |
Sắp xếp nhanh (Quicksort), còn gọi là phương pháp sắp xếp phân chia (part sort), là thuật toán được phát triển bởi C.A.R. Hoare. Thuật toán này chia danh sách cần sắp xếp thành hai danh sách con. Khác với phương pháp sắp xếp trộn, được chia thành hai danh sách con có kích thước gần bằng nhau bằng cách chọn một phần tử chốt. Các phần tử nhỏ hơn hoặc bằng phần tử chốt được đưa về phía trước và nằm trong danh sách con thứ nhất, trong khi các phần tử lớn hơn phần tử chốt được đưa về phía sau và nằm trong danh sách con thứ hai. Quá trình này tiếp tục cho đến khi các danh sách con có độ dài bằng 1.
Phần tử chốt (pivot)
Kỹ thuật chọn phần tử chốt ảnh hưởng lớn đến khả năng xảy ra vòng lặp vô hạn trong các trường hợp đặc biệt. Tốt nhất là chọn phần tử chốt làm trung vị của danh sách. Khi đó, sau lần phân chia, ta sẽ đạt kích thước danh sách bằng 1. Tuy nhiên, điều này rất khó thực hiện. Có một số phương pháp để chọn phần tử chốt như sau:
- Chọn phần tử đầu tiên hoặc cuối cùng làm phần tử chốt.
- Chọn phần tử ở giữa danh sách làm phần tử chốt.
- Chọn phần tử trung bình trong ba phần tử đầu tiên, giữa và cuối cùng làm phần tử chốt.
- Chọn phần tử ngẫu nhiên làm phần tử chốt (phương pháp này có thể dẫn đến những tình huống đặc biệt).
Quy trình phân chia
Sau khi chọn phần tử chốt, thuật toán phân chia nên được thực hiện như thế nào?
- Một phương pháp đơn giản là so sánh từng phần tử từ đầu đến cuối danh sách với phần tử chốt. Phương pháp này yêu cầu thực hiện n phép so sánh và cần n đơn vị bộ nhớ để lưu trữ các giá trị trung gian.
- Phương pháp khác là duyệt danh sách từ hai hướng: từ đầu danh sách và từ cuối danh sách. Tìm phần tử đầu tiên từ trái lớn hơn phần tử chốt và phần tử đầu tiên từ phải nhỏ hơn hoặc bằng phần tử chốt, rồi hoán đổi chúng. Tiếp tục cho đến khi hai hướng gặp nhau.
- Để thực hiện đệ quy, ta phân chia danh sách con thành hai danh sách.
Ví dụ
Trong ví dụ dưới đây, chúng ta luôn chọn phần tử chốt là phần tử ở giữa danh sách, với chỉ số của phần tử chốt được tính theo công thức
| 2 | 6 | 3 | 7 | 4 | 5 | 1 |
Vì phần tử chốt là phần tử lớn nhất trong dãy, không tìm thấy phần tử nào lớn hơn phần tử chốt khi duyệt từ trái sang phải. Do đó, ta sẽ hoán đổi phần tử chốt với phần tử cuối cùng, dẫn đến việc chia danh sách thành hai phần: và
| 2 | 6 | 3 | 1 | 4 | 5 | -- | 7 |
Quá trình phân chia tiếp tục với danh sách con . Lần này, phần tử chốt được chọn là a[4]=1. Tìm từ trái sang phải, phần tử đầu tiên lớn hơn là . Từ phải sang trái, phần tử đầu tiên nhỏ hơn hoặc bằng 1 là chính a[4]. Ta hoán đổi hai phần tử này
| 1 | 6 | 3 | 2 | 4 | 5 | -- | 7 |
Khi tiếp tục duyệt sang phải, ta thấy . Trong khi đó, từ phía ngược lại, ta tìm thấy phần tử nhỏ hơn hoặc bằng phần tử chốt là . Khi hai đường đã gặp nhau, ta không thực hiện thêm hoán đổi. Kết quả là được chia thành hai danh sách con và
| 1 | -- | 6 | 3 | 2 | 4 | 5 | -- | 7 |
Tiếp tục phân chia danh sách với phần tử chốt 2. Chúng ta sẽ nhận được kết quả là
| 1 | -- | 2 | -- | 3 | 6 | 4 | 5 | -- | 7 |
Tiếp tục quá trình phân chia danh sách với phần tử chốt là
| 1 | -- | 2 | -- | 3 | 4 | -- | 6 | 5 | -- | 7 |
Tiếp tục phân chia danh sách với phần tử chốt là và phân chia tiếp theo là với phần tử chốt
| 1 | -- | 2 | -- | 3 | -- | 4 | -- | 5 | -- | 6 | -- | 7 |
Mã giả
Quá trình phân chia
// left là chỉ số của phần tử đầu tiên của mảng
// right là chỉ số của phần tử cuối cùng của mảng
// số phần tử của mảng = right-left+1
function partition(array, 'left', 'right', 'pivotIndex')
1.'pivotValue':= array['pivotIndex']
2.swap array['pivotIndex'] và array['right'] // Đưa pivot đến cuối mảng
3.'storeIndex':= 'left'
4.for 'i' từ 'left' đến 'right'-1 // left ≤ i < right
1.nếu array['i'] < 'pivotValue'
1.swap array['i'] và array['storeIndex']
2.'storeIndex':= 'storeIndex' + 1
5.swap array['storeIndex'] và array['right'] // Đưa pivot về vị trí cuối cùng
6.return 'storeIndex'
Thuật toán sắp xếp nhanh sử dụng đệ quy
function quicksort(array, 'left', 'right')
// Nếu danh sách có từ 2 phần tử trở lên
if 'left' < 'right'
// Xem phần 'Lựa chọn pivot' bên dưới để chọn pivot
chọn bất kỳ 'pivotIndex' nào sao cho 'left' ≤ 'pivotIndex' ≤ 'right'
// Xác định các phần tử lớn hơn và nhỏ hơn pivot và vị trí cuối cùng của pivot
'pivotNewIndex':= partition(array, 'left', 'right', 'pivotIndex')
// Đệ quy sắp xếp các phần tử nhỏ hơn pivot
quicksort(array, 'left', 'pivotNewIndex' - 1)
// Đệ quy sắp xếp các phần tử lớn hơn hoặc bằng pivot
quicksort(array, 'pivotNewIndex' + 1, 'right')
Thuật toán sắp xếp nhanh đệ quy với cấu trúc dữ liệu C
#include<stdio.h> #include<conio.h> typedef int keytype; typedef struct{ keytype key; }recordtype; void Swap(recordtype *x, recordtype *y){ recordtype temp; temp = *x; *x = *y; *y = temp; } int FindPivot(recordtype a[],int i, int j){ keytype firstkey; int k; k=i+1; firstkey = a[i].key; while((k<=j)&&(a[k].key==firstkey)) k++; if(k>j) return -1; else if((a[k].key > firstkey)) return k; else return i; } int Partition(recordtype a[],int i, int j, keytype pivot){ int L, R; L=i; R=j; while(L<=R){ while (a[L].key < pivot) L++; while (a[R].key > pivot) R--; if (L < R) Swap(&a[L], &a[R]); } return L; } void QuickSort (recordtype a[], int i, int j){ keytype pivot; int pivotindex, k; pivotindex = FindPivot(a,i, j); if (pivotindex != -1){ pivot = a[pivotindex].key; k = Partition(a, i, j, pivot); QuickSort(a, i, k-1); QuickSort(a, k, j); } } int main(){ int n,i; recordtype a[50]; printf('nhap n: '); scanf('%d',&n); for(i=0;i<n;i++){ printf('nhap phan tu: '); scanf('%d',&a[i].key); } QuickSort(a, 0, n-1); for(i= 0;i<n;i++){ printf(' --- %d',a[i].key); } return 0; }
Thuật toán sắp xếp không sử dụng đệ quy
Nhiều người cho rằng việc loại bỏ đệ quy trong thuật toán sắp xếp nhanh không thực sự cần thiết, mà chỉ giúp những người mới học khoa học máy tính hiểu rõ hơn về khái niệm đệ quy. Thực chất, các thuật toán đệ quy lưu trữ các tham số đệ quy vào ngăn xếp để xử lý lần lượt.
Khi chuyển đổi thuật toán đệ quy sang dạng không đệ quy, mỗi lần chia danh sách thành hai phần, ta sẽ lưu trữ các tham số của phần sau vào ngăn xếp và tiếp tục chia phần trước.
Một cách đơn giản để chuyển đổi thuật toán sắp xếp nhanh từ đệ quy sang không đệ quy như sau:
Procedure QuickSort(a[1..n]) {
Var list S, E; Int m:=1
S(m):=1; E(m):= n;
While m>0 {
k=S(m); l=E(m)
m:=m-1;
if l<k then {
i=Part(k,l);
m=m+1;
S(m):=i+1
E(m):=l
}
}
}
Thuật toán sắp xếp nhanh không đệ quy có những ưu điểm rõ ràng nhờ vào các cải tiến. Có thể tối ưu hóa thêm bằng cách lưu trữ phần danh sách con nhỏ hơn trong hai phần và sử dụng phương pháp sắp xếp đơn giản hơn cho các phần danh sách có kích thước nhỏ.
Sắp xếp nhanh phân chia thành ba phần
Một cách phân chia khác là chia danh sách thành ba phần con: nhỏ hơn, bằng và lớn hơn phần tử chốt.
function quicksort(a)
Var list less, equal, greater
if length(a) ≤ 1
return a
else
select a pivot value pivot from a
for each x in a
if x < pivot then add x to less
if x = pivot then add x to equal
if x > pivot then add x to greater
return concatenate(quicksort(less), equal, quicksort(greater))
- Sắp xếp nổi bọt
- Sắp xếp chọn
- Sắp xếp chèn
- Sắp xếp trộn
- Sắp xếp vun đống
