
Toán học cung cấp cho các học sinh, sinh viên những kiến thức quan trọng để áp dụng vào thực tế. Ngoài các số tự nhiên và số nguyên đơn giản, người học sẽ tiếp cận với khái niệm số hữu tỉ và số vô tỉ. Tập hợp các số này rộng lớn và xuất hiện nhiều trong các vấn đề thực tế. Vậy số hữu tỉ là gì và số vô tỉ là gì? Sự khác nhau của hai loại số này có thể được phân biệt như thế nào? Hãy cùng Mytour khám phá về kiến thức Toán học hữu ích trong bài viết ngày hôm nay nhé!
Tổng quan về số hữu tỉ trong Toán học
Theo chương trình học hiện nay, học sinh được giới thiệu với số hữu tỉ từ cấp Tiểu học, và học sâu hơn về các phép tính và công thức liên quan đến loại số này từ THCS đến THPT. Số hữu tỉ là một kiến thức cực kỳ quan trọng, là nền tảng cho việc phát triển tư duy và giải quyết các bài tập phức tạp hơn trong tương lai. Phần đầu của bài viết sẽ cung cấp các thông tin cơ bản về số hữu tỉ cho độc giả.
Số hữu tỉ là gì? Ý nghĩa của số hữu tỉ
Số hữu tỉ là một tập hợp các số có thể biểu diễn dưới dạng phân số a/b, với điều kiện cả a và b là số nguyên (bao gồm cả số âm và dương), và b khác 0. Đây là quy ước cơ bản trong Toán học để đảm bảo tính hợp lệ của phân số. Trường hợp b = 0 sẽ dẫn đến số hữu tỉ trở thành số vô nghĩa. Khái niệm này được sử dụng phổ biến trong giáo dục Toán học để giới thiệu cho học sinh về các phép tính và ứng dụng thực tiễn của số hữu tỉ.
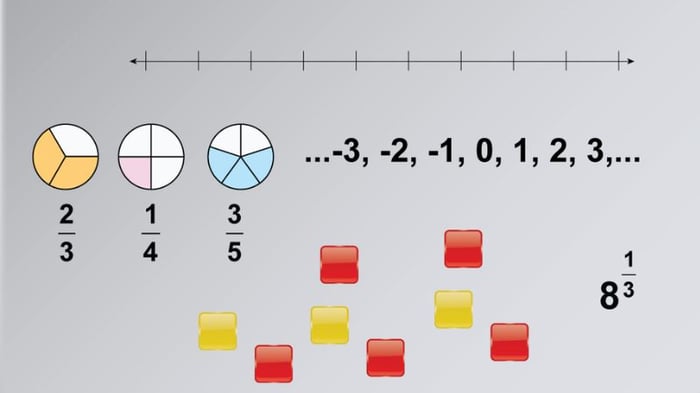
Số hữu tỉ là gì và vì sao nó quan trọng không chỉ trong Toán học mà còn trong các môn học tự nhiên như Vật lý, Hóa học, và Sinh học? Loại số này cho phép mô tả rõ ràng các tỷ lệ, cách chia phần và các khái niệm liên quan. Nó được sử dụng từ khi khái niệm phân số ra đời và có thể biểu diễn dưới dạng số thập phân với dấu chấm phân cách phần nguyên và phần thập phân. Tuy nhiên, để dễ hiểu, thường sử dụng biểu diễn a/b (a, b là số nguyên và b khác 0).
Khái quát về tập hợp các số hữu tỉ
Tập hợp các số hữu tỉ được biểu diễn là ℚ với dạng chữ in đậm hoặc viết tắt Q, xuất phát từ từ quoziente có nghĩa là tỷ lệ. Tập hợp các số hữu tỉ là một phần của tập số thực ℝ, bao gồm tất cả các số hữu tỉ và mở rộng hơn nữa để bao gồm các số tự nhiên ℕ và số nguyên ℤ. Những tính chất cơ bản của tập hợp ℚ bao gồm việc nó là tập hợp số có thể đếm được, bao gồm cả số nguyên, số thập phân hữu hạn và vô hạn tuần hoàn.
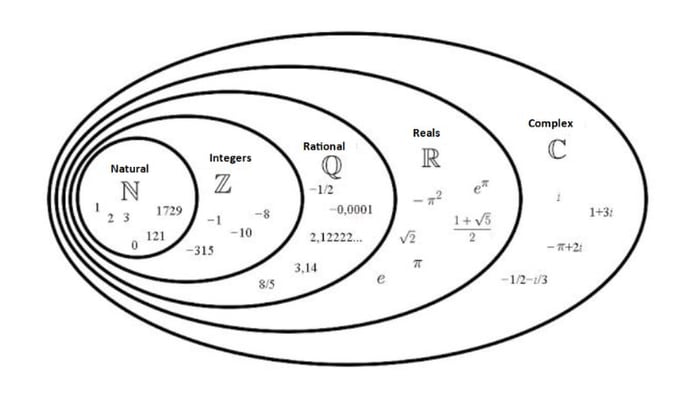
Khái niệm về tập hợp số hữu tỉ được đơn giản hóa trong Toán học bằng cách viết tắt: Q = {a/b; a, b là số nguyên 𝕫 ; b khác 0}. Đây cũng là cách biểu diễn phần tử của tập hợp này trên một trục số, với việc sử dụng dấu phân cách để thể hiện rõ ràng số. Học sinh cần phải nhớ các ký hiệu này để tránh nhầm lẫn trong giải bài tập và ứng dụng thực tế. Đồng thời, hiểu rõ về bản chất của số hữu tỉ để phân biệt chính xác với số vô tỉ hoặc số ảo.
Giá trị tuyệt đối của số hữu tỉ là gì?
Tương tự như số nguyên, giá trị tuyệt đối của số hữu tỉ là khoảng cách từ số đó đến gốc 0 trên trục số. Nói một cách đơn giản, giá trị tuyệt đối của số hữu tỉ là phần dương của số đó, ngoại trừ trường hợp số 0 vì giá trị tuyệt đối của 0 chính là chính nó. Định nghĩa này có thể được biểu thị bằng ký hiệu: |x| với x thuộc Q.

Theo quy ước, giá trị tuyệt đối của một số hữu tỉ x được tính như sau:
- |x| = 0 nếu x = 0
- |x| = x nếu x > 0, tức x là số dương
- |x| = -x nếu x < 0, tức x là số âm
Khái niệm giá trị tuyệt đối rất hữu ích khi so sánh các số hữu tỉ âm, giúp loại bỏ dấu “-” khi tính toán. Cách tính toán và so sánh này là một chiêu thức hữu ích giúp bạn nhanh chóng và chính xác hơn khi làm các bài toán về các số âm.
Phân loại các loại số hữu tỉ
Sau khi đã hiểu rõ về khái niệm số hữu tỉ là gì, bạn có thể khám phá sâu hơn về các loại số hữu tỉ. Mỗi loại có đặc điểm và vị trí riêng trên trục số, biểu thị các tỷ lệ khác nhau. Dựa trên nguyên tắc tập hợp con của tập Q, số hữu tỉ có thể được chia thành 4 loại:
Số nguyên: Bao gồm các số chỉ có phần nguyên và có thể được biểu thị dưới dạng phân số là x/1 với x 𝕫, bao gồm cả số nguyên âm và dương.
Số thập phân hữu hạn: Đây là dạng số hữu tỉ có mẫu số là một số nguyên dương như 2 và 5 (khi đó là phân số tối giản), được biểu diễn dưới dạng số thập phân hữu hạn (có số chữ số hữu hạn ở phần thập phân).

Số thập phân vô hạn tuần hoàn: Đây là dạng số hữu tỉ khi biểu thị dưới dạng phân số tối giản có mẫu số là số nguyên dương và khác 2, 5. Khi đó, phân số sẽ được biểu diễn dưới dạng số thập phân vô hạn tuần hoàn (phần thập phân không giới hạn và có tính lặp lại).
Số 0: Đây là một số hữu tỉ đặc biệt, không thuộc vào bất kỳ nhóm số hữu tỉ âm hay dương nào.
Các phép toán liên quan đến số hữu tỉ
Như vậy, các khái niệm và ký hiệu liên quan đã được cung cấp đầy đủ để bạn hiểu rõ hơn về số hữu tỉ. Để giải các bài toán trong Toán học và các môn khác, người học cần nắm bắt thêm các công thức tính toán và cách so sánh số hữu tỉ. Những phương pháp tính toán này tương tự như các số nguyên và số tự nhiên, nhưng áp dụng cho phân số. Hơn nữa, trước khi nghiên cứu về các phép toán này, bạn cũng cần ghi nhớ một số tính chất như nguyên tắc số đối, số đối của số hữu tỉ âm là số hữu tỉ dương và ngược lại, tổng của 2 số đối nhau bằng 0 và nguyên tắc đảo ngược trong phép chia và không chia được cho 0.
Công thức tính số hữu tỉ là gì?
Các công thức dưới đây áp dụng cho các số hữu tỉ X và Y, được biểu diễn dưới dạng phân số với tử và mẫu là số nguyên, mẫu khác 0. Các công thức này tập trung vào các phép tính lũy thừa của số hữu tỉ, vì các phép cộng, trừ, nhân, chia khá đơn giản và dễ hiểu. Các phép tính này có thể được biểu diễn như sau:
- Phép cộng hai số hữu tỉ có cùng mẫu: Thực hiện cộng tử số với nhau và giữ nguyên mẫu số, sau đó rút gọn phân số thành dạng tối giản.
- Phép cộng hai số hữu tỉ khác mẫu: Thực hiện quy đồng mẫu số, chuyển hai phân số về cùng mẫu rồi thực hiện phép cộng.
- Phép trừ hai số hữu tỉ cùng và khác mẫu: Thực hiện phép tính tương tự phép cộng, nhưng lấy tử số của số bị trừ trừ đi số trừ để thu được kết quả.
- Phép nhân hai số hữu tỉ: Thực hiện nhân tử với tử, mẫu với mẫu của hai phân số, sau đó rút gọn để có phân số tối giản. Chú ý rằng số nhân với 1 bằng chính nó và số nhân với 0 bằng 0.
- Phép chia hai số hữu tỉ: Thực hiện nhân tử với tử, mẫu với mẫu của số bị chia với phân số nghịch đảo của số chia, sau đó rút gọn để thu được kết quả là phân số tối giản.

Vậy công thức tính lũy thừa của số hữu tỉ là gì? Đối với phép tính lũy thừa, bạn đọc cần nhớ và nắm vững 4 công thức quan trọng được đề cập trong hình ảnh ở phía trên.
Cách so sánh các số hữu tỉ với nhau
Khi so sánh 2 số hữu tỉ, có 2 trường hợp xảy ra: so sánh phân số cùng mẫu và so sánh phân số khác nhau.
Đối với trường hợp cùng mẫu và là số hữu tỉ dương, số nào có tử số lớn hơn thì sẽ lớn hơn. Ngược lại, đối với trường hợp cùng mẫu và là số hữu tỉ âm, số nào có giá trị tuyệt đối lớn hơn thì nhỏ hơn.
Trong trường hợp so sánh số hữu tỉ khác mẫu, bạn cần tiến hành quy đồng mẫu số, đưa cả 2 phân số cần so sánh về cùng mẫu rồi tiến hành các bước giống với trường hợp cùng mẫu.
Số vô tỉ là gì? Bản chất của số vô tỉ trong Toán học
Nếu đã biết số hữu tỉ là gì, người học chỉ cần nhớ đơn giản rằng số vô tỉ là dạng ngược lại so với số hữu tỉ. Cụ thể, số vô tỉ là tập hợp số được viết dưới dạng số thập phân vô hạn không tuần hoàn (phần sau dấu phẩy không giới hạn và không có tính chất lặp lại giữa các chữ số). Tập hợp các số vô tỉ được ký hiệu là I, cũng là một tập hợp con của số thực R. Số vô tỉ là tập hợp số không đếm được và rất khó để thể hiện chính xác số đó trên trục số. Một vài dạng số vô tỉ đặc biệt có thể kể đến như , căn bậc hai của các số ngoài số chính phương hoặc kết quả từ các phép tính log, lượng giác…

Vậy điểm khác biệt giữa số hữu tỉ và số vô tỉ là gì? Nhìn vào tính chất và các quy ước về cách viết, có thể dễ dàng phân biệt hai loại số này theo những tiêu chí sau đây:
- Số hữu tỉ có thể được biểu diễn dưới dạng phân số với tử và mẫu là số nguyên, mẫu khác 0; số vô tỉ được biểu diễn dưới dạng số thập phân với phần sau dấu phẩy không giới hạn số chữ số.
- Số hữu tỉ có thể là số nguyên, số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn; số vô tỉ là số thập phân vô hạn không tuần hoàn.
- Tập hợp số hữu tỉ có thể đếm được và có thể biểu diễn trên trục số; tập hợp số vô tỉ không thể đếm được và rất khó để biểu diễn chính xác trên trục số.
Tổng kết về chủ đề “Số hữu tỉ và số vô tỉ là gì?”
Toán học là một lĩnh vực rộng lớn và hấp dẫn khi bạn khám phá các con số kỳ diệu, các không gian và hình học thực tế. Các khái niệm đơn giản nhưng lại là nền tảng để xây dựng và phát triển kiến thức chuyên sâu và phức tạp hơn. Số hữu tỉ và số vô tỉ là ví dụ điển hình. Những lý thuyết, công thức và tính chất của chúng rất dễ hiểu và có thể áp dụng vào các bài toán phức tạp như lượng giác, logarit, tích phân, nguyên hàm, tính diện tích và thể tích trong không gian.
Như vậy, bài viết đã giới thiệu đầy đủ thông tin cần thiết để hiểu rõ hơn về số hữu tỉ và số vô tỉ cùng các công thức tính toán liên quan. Để thành thạo trong môn Toán học, hãy hiểu sâu hơn về bản chất của những con số này và áp dụng chúng một cách thành thạo khi giải các bài tập. Hi vọng rằng với những kiến thức này, bạn sẽ có được nền tảng vững chắc hơn trong môn học thú vị này. Đừng quên theo dõi Mytour để cập nhật những tin tức và thủ thuật công nghệ mới nhất.
