Số nguyên tố Mersenne

Số nguyên tố Mersenne là một loại số nguyên tố có dạng 2^p - 1, với p là một số nguyên tố. Ví dụ, số 31 là số nguyên tố Mersenne vì 31 = 2^5 - 1 (31 và 5 đều là số nguyên tố).

Để số M_n là số nguyên tố, n cần phải là một số nguyên tố. Tuy nhiên, 2^4 - 1 = 15 không phải là số nguyên tố vì 4 không phải là số nguyên tố. Ngược lại, ví dụ như số 2047 = 2^11 - 1 không phải là số nguyên tố vì nó chia hết cho 89 và 23, mặc dù số 11 là số nguyên tố.

Ngày nay, các số nguyên tố lớn nhất thường là các số nguyên tố Mersenne.

Số nguyên tố Mersenne có mối liên hệ mật thiết với các số hoàn thiện, tức là các số bằng tổng các ước số của chính nó. Trong quá khứ, việc nghiên cứu số nguyên tố Mersenne đã dẫn đến những thay đổi quan trọng; vào thế kỷ IV TCN, Euclid đã cho rằng nếu M là số nguyên tố Mersenne thì M(M+1)/2 là số hoàn thiện. Đến thế kỷ XVIII, Leonhard Euler đã chứng minh rằng tất cả các số hoàn thiện chẵn đều có dạng này. Hiện tại, chưa có số hoàn thiện lẻ nào được biết đến, và vẫn chưa rõ liệu chúng có tồn tại hay không.

Khám phá các số nguyên tố Mersenne

Công thức sau đây

$2^{ab}-<!--\; -\; -->1=(2^a-<!--\; -\; -->1)\cdot <!--\; \cdot \; -->\left(1+2^a+2^{2a}+2^{3a}+\cdots <!--\; \cdots \; -->+2^{(b-<!--\; -\; -->1)a}\right)$

Một số nguyên tố Mersenne chỉ có thể là số nguyên tố nếu n là số nguyên tố. Điều này giúp đơn giản hóa việc tìm kiếm số nguyên tố Mersenne. Tuy nhiên, điều ngược lại không đúng: số Mn không nhất thiết là số nguyên tố chỉ vì n là số nguyên tố. Ví dụ, 2^11 - 1 = 2047 không phải là số nguyên tố mà phân tích được thành 23 x 89, mặc dù 11 là số nguyên tố.

Đã có nhiều thuật toán được tối ưu hóa để tìm số nguyên tố Mersenne, vì vậy hiện nay người ta đã phát hiện ra các số nguyên tố Mersenne cực kỳ lớn.

Bốn số nguyên tố Mersenne đầu tiên đã được biết đến từ lâu bao gồm $M_2=3$, $M_3=7$, $M_5=31$ và $M_7=127$. Số nguyên tố thứ năm, $M_{13}=8191$ được phát hiện trước năm 1461. Hai số tiếp theo là $M_{17}$ và $M_{19}$ được Cataldi phát hiện vào năm 1588. Ông cũng dự đoán các số mũ 23 (bị Fermat bác bỏ), 29 (bị Fermat bác bỏ), và 37 (bị Euler bác bỏ). Hơn một thế kỷ sau, $M_{31}$ được Euler kiểm tra vào năm 1750 bằng phương pháp Lý thuyết chỉ số. Số tiếp theo là $M_{127}$, được Lucas tìm thấy vào năm 1876, sau đó là $M_{61}$ do Pervushin phát hiện vào năm 1883. Hai số nữa là $M_{89}$ và $M_{107}$ được phát hiện vào thế kỷ XX bởi Powers vào năm 1911 và 1914.

Từ thế kỷ XVII, các số Mersenne đã được đặt tên theo nhà toán học Pháp Marin Mersenne, người đã chứng minh và dự đoán nhiều số nguyên tố Mersenne với các số mũ: 2, 3, 5, 7, 13, 17, 31, 67, 127, 257. Danh sách của ông không hoàn toàn chính xác, vì ông bao gồm cả M₆₇ (được Kohler chứng minh là hợp số vào năm 1901, cụ thể: $2^{67}-<!--\; -\; -->1=\mathrm{193.707.721}\times <!--\; \times \; -->\mathrm{761.838.257.287}$), M₂₅₇ (được chứng minh là hợp số vào năm 1952), và đã bỏ sót M₆₁, M₈₉ và M₁₀₇.

Phương pháp hiệu quả nhất để kiểm tra tính nguyên tố của các số Mersenne dựa trên một chuỗi tuần hoàn, được Lucas đề xuất vào năm 1878 và chứng minh bởi Lehmer trong những năm 1930. Phương pháp này hiện được gọi là kiểm tra Lucas-Lehmer cho số Mersenne. Cụ thể, số $M_n=2^n-<!--\; -\; -->1$ là số nguyên tố nếu và chỉ nếu nó chia hết cho Sn-2, với $S_0=4$ và với $k>0$, $S_k=S_{k-<!--\; -\; -->1}^2-<!--\; -\; -->2$.

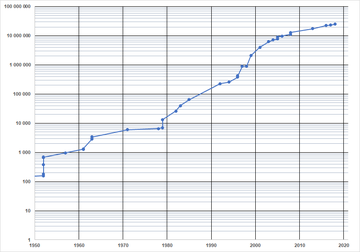
Việc phát hiện các số nguyên tố Mersenne đã có sự tiến bộ đáng kể nhờ vào máy tính điện tử. Đột phá đầu tiên trong lĩnh vực này là số nguyên tố Mersenne M₅₂₁, được phát hiện vào lúc 10:00 P.M. ngày 30 tháng 1 năm 1952 bằng máy tính tự động SWAC của Cục Tiêu chuẩn Quốc gia Mỹ tại Viện Phân Tích Số thuộc Đại học California, Los Angeles. Dưới sự chỉ đạo của Lehmer và chương trình do GS R.M. Robinson viết, đây là số nguyên tố Mersenne đầu tiên tìm thấy sau 38 năm. Số tiếp theo, M₆₀₇, được phát hiện chỉ sau gần hai giờ chạy máy. Các số tiếp theo như M₁₂₇₉, M₂₂₀₃, và M₂₂₈₁ cũng được phát hiện nhờ chương trình này sau nhiều tháng. M₄₂₅₃ là số nguyên tố Mersenne đầu tiên vượt qua 1000 chữ số, còn M₄₄₄₉₇ là số đầu tiên có trên 10.000 chữ số.

Tính đến tháng 9 năm 2008, đã phát hiện được 46 số nguyên tố Mersenne, trong đó số lớn nhất là (2 − 1). Giống như nhiều số nguyên tố Mersenne trước đó, nó được phát hiện nhờ vào dự án tính toán phân tán qua Internet, được gọi là Tìm kiếm số nguyên tố Mersenne khổng lồ trên Internet (Great Internet Mersenne Prime Search - GIMPS).

Các định lý về số nguyên tố Mersenne

• Nếu n là số nguyên dương, theo định lý nhị thức, ta có thể viết:

$c^n-<!--\; -\; -->d^n=(c-<!--\; -\; -->d)\underset{k=0}{\overset{n-<!--\; -\; -->1}{\sum <!--\; \sum \; -->}}{c}^k{d}^{n-<!--\; -\; -->1-<!--\; -\; -->k}$,

hay

$(2^a-<!--\; -\; -->1)\cdot <!--\; \cdot \; -->\left(1+2^a+2^{2a}+2^{3a}+\cdots <!--\; \cdots \; -->+2^{(b-<!--\; -\; -->1)a}\right)=2^{ab}-<!--\; -\; -->1$

Bằng cách đặt $c=2^a$, $d=1$, và $n=b$

Chứng minh:

$(a-<!--\; -\; -->b)\underset{k=0}{\overset{n-<!--\; -\; -->1}{\sum <!--\; \sum \; -->}}{a}^k{b}^{n-<!--\; -\; -->1-<!--\; -\; -->k}$

$=\underset{k=0}{\overset{n-<!--\; -\; -->1}{\sum <!--\; \sum \; -->}}{a}^{k+1}{b}^{n-<!--\; -\; -->1-<!--\; -\; -->k}-<!--\; -\; -->\underset{k=0}{\overset{n-<!--\; -\; -->1}{\sum <!--\; \sum \; -->}}{a}^k{b}^{n-<!--\; -\; -->k}$

$=a^n+\underset{k=1}{\overset{n-<!--\; -\; -->1}{\sum <!--\; \sum \; -->}}{a}^k{b}^{n-<!--\; -\; -->k}-<!--\; -\; -->\underset{k=1}{\overset{n-<!--\; -\; -->1}{\sum <!--\; \sum \; -->}}{a}^k{b}^{n-<!--\; -\; -->k}-<!--\; -\; -->b^n$

$=a^n-<!--\; -\; -->b^n$

• Nếu $2^n-<!--\; -\; -->1$ là một số nguyên tố, thì $n$ cũng là số nguyên tố.

Chứng minh:

Do

$(2^a-<!--\; -\; -->1)\cdot <!--\; \cdot \; -->\left(1+2^a+2^{2a}+2^{3a}+\cdots <!--\; \cdots \; -->+2^{(b-<!--\; -\; -->1)a}\right)=2^{ab}-<!--\; -\; -->1$

Nếu $n$ không phải là số nguyên tố, hoặc $n=ab$ với . Vậy, $2^a-<!--\; -\; -->1$ là ước của $2^n-<!--\; -\; -->1$, hoặc $2^n-<!--\; -\; -->1$ không phải là số nguyên tố.

• Với mọi số nguyên tố lẻ p, các ước nguyên tố của M_p đều có dạng $2kp+1\equiv <!--\; \equiv \; -->\pm <!--\; \pm \; -->1\left(\mathrm{mod}8\right)$.

Chứng minh

Gọi q là một ước nguyên tố của số 2 - 1 thì ta có:

$2^p\equiv <!--\; \equiv \; -->1\left(\mathrm{mod}q\right)$.

Dựa vào định lý nhỏ Fermat, ta có:

$2^{q-<!--\; -\; -->1}\equiv <!--\; \equiv \; -->1\left(\mathrm{mod}q\right)$.

Từ đó, q là ước chung của các số 2 - 1 và 2 - 1, hay nói cách khác, $gcd(2^p-<!--\; -\; -->1,2^{q-<!--\; -\; -->1}-<!--\; -\; -->1)>1$(*).

Xét bổ đề sau: Nếu a và b là hai số nguyên dương khác nhau thì $gcd(2^a-<!--\; -\; -->1,2^b-<!--\; -\; -->1)=2^{gcd(a,b)}-<!--\; -\; -->1$.

Đúng vậy, giả sử $gcd(a,b)=d$, từ đó a = k₁d và b = k₂d.

Kết luận rằng:

$2^a-<!--\; -\; -->1=2^{k_{1}d}-<!--\; -\; -->1=\left(2^d-<!--\; -\; -->1\right)\times <!--\; \times \; -->A$

$2^b-<!--\; -\; -->1=2^{k_{2}d}-<!--\; -\; -->1=\left(2^d-<!--\; -\; -->1\right)\times <!--\; \times \; -->B$

Như vậy, bổ đề chúng ta đưa ra là chính xác.

Từ bổ đề trên, ta có: $gcd(2^p-<!--\; -\; -->1,2^{q-<!--\; -\; -->1}-<!--\; -\; -->1)=2^{gcd(p,q-<!--\; -\; -->1)}-<!--\; -\; -->1$.

Giả sử $gcd(p,q-<!--\; -\; -->1)=1$ thì có thể suy ra $gcd(2^p-<!--\; -\; -->1,2^{q-<!--\; -\; -->1}-<!--\; -\; -->1)=1$, điều này mâu thuẫn với (*). Do đó, cần phải có $gcd(p,q-<!--\; -\; -->1)>1$. Vì p là số nguyên tố nên $gcd(p,q-<!--\; -\; -->1)=p$ tức là q - 1 = bp.

Vì q là ước của M_p lẻ nên q phải là số lẻ, do đó b = 2k và q = 2kp + 1.

Do 2 ≡ 1 (mod q) nên 2 ≡ 2 (mod q), từ đó $2^{\frac{p+1}{2}}$ là căn bậc hai của 2 theo modulo (môđun) q, hay nó là nghiệm của phương trình:

$x^2\equiv <!--\; \equiv \; -->2\left(\mathrm{mod}q\right)$.

Theo định lý tương hỗ bậc hai:

$q\equiv <!--\; \equiv \; -->\pm <!--\; \pm \; -->1\left(\mathrm{mod}8\right)$.

Danh sách các số nguyên tố Mersenne đã được phát hiện cho đến nay

Tính đến tháng 12 năm 2021, đã có 51 số nguyên tố Mersenne dạng 2^p - 1 với các số mũ p như sau:

2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609, 57885161, 74207281, 77232917, 82589933. (dãy số A000043 trong bảng OEIS)

• Để hình dung kích thước của số nguyên tố lớn nhất từng được phát hiện (số thứ 48), cần tới 4.647 tờ giấy A4 nếu in số đó với định dạng 75 chữ số mỗi dòng và 50 dòng mỗi trang. Sử dụng giấy định lượng 70g/m², bạn sẽ cần hơn 10 kg giấy (2.324 tờ), tạo thành một tập dày khoảng 20 cm.
• Nếu nhân hai số lũy thừa n trừ 1 với nhau, bạn sẽ có một số hoàn hảo.

• Repunit
• Số nguyên tố Fermat
• Hằng số Erdős–Borwein
• Prime95 / MPrime
• Kiểm tra Lucas–Lehmer cho các số Mersenne
• Số Mersenne kép
• Mersenne twister
• Bảng số nguyên tố

Liên kết ngoài

• Great Internet Mersenne Prime Search (GIMPS), Orlando, Florida
  • Báo cáo cột mốc GIMPS PrimeNet (v5.0)
• Số Mersenne – Lịch sử, Định lý và Danh sách – giải thích
• Số Mersenne – Wolfram Research/Mathematica
• Số Mersenne nguyên tố – Wolfram Research/Mathematica
• Mq = (8x) - (3qy) Chứng minh số Mersenne (pdf)
• Mq = x + d.y Luận văn toán học Lưu trữ 2005-02-21 tại Wayback Machine (ps)
• Danh mục tài liệu về số Mersenne và số nguyên tố Mersenne với liên kết đến các ấn phẩm gốc
• Primzahl ist 39 Kilometer lang, 11.03.2005.dpa – bài báo về số nguyên tố Mersenne – phát hiện chi tiết (tiếng Đức)
• Wiki số nguyên tố Mersenne Lưu trữ 2006-12-05 tại Wayback Machine
• Số nguyên tố Mersenne thứ 43 được tìm thấy tại MathWorld