Số phức

Số phức (tiếng Anh: Complex number) là một số có thể được biểu diễn dưới dạng a + b ı {displaystyle a+bimath } , trong đó a và b là các số thực, $\mathrm{ı<!--\; ı\; -->}$ là đơn vị ảo, với ${\mathrm{ı<!--\; ı\; -->}}^2=-<!--\; -\; -->1$ hoặc $\mathrm{ı<!--\; ı\; -->}=\sqrt{-<!--\; -\; -->1}$. Trong biểu thức này, số a được gọi là phần thực và b là phần ảo của số phức. Số phức có thể được biểu diễn trên mặt phẳng số phức với trục hoành là trục thực và trục tung là trục ảo, do đó một số phức $a+b\mathrm{ı<!--\; ı\; -->}$ tương ứng với một điểm có tọa độ (a,b). Nếu số phức có phần thực bằng không thì được gọi là số thuần ảo (hay số ảo), còn nếu phần ảo bằng không thì trở thành số thực R. Trường số phức được mở rộng để giải quyết các bài toán không thể giải trong trường số thực.

Số phức có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học, chẳng hạn như kỹ thuật, điện từ học, cơ học lượng tử, và toán học ứng dụng, bao gồm lý thuyết hỗn loạn. Gerolamo Cardano, một nhà toán học người Ý, là người đầu tiên đưa ra số phức và áp dụng chúng để giải các phương trình bậc ba vào thế kỉ 16.

Lịch sử

Nhà toán học người Ý R. Bombelli (1526-1573) đã lần đầu tiên định nghĩa số phức, khi đó được gọi là số 'không thể có' hoặc 'số ảo' trong tác phẩm Đại số (Bologna, 1572) được công bố không lâu trước khi ông qua đời. Ông đã đưa ra định nghĩa cho các số phức khi nghiên cứu phương trình bậc ba và xác định căn bậc hai của $-<!--\; -\; -->1$.

Nhà toán học người Pháp D’Alembert vào năm 1746 đã xác định được dạng tổng quát '$a+b\mathrm{ı<!--\; ı\; -->}$' của số phức, đồng thời công nhận nguyên lý rằng một phương trình bậc n luôn có n nghiệm. Nhà toán học Thụy Sĩ L. Euler (1707-1783) đã giới thiệu ký hiệu '$\mathrm{ı<!--\; ı\; -->}$' để chỉ căn bậc hai của $-<!--\; -\; -->1$, và ký hiệu này đã được Gauss tiếp tục sử dụng vào năm 1801.

Tổng quan

Số phức cho phép giải các phương trình mà không thể giải trong trường số thực. Ví dụ, phương trình

${\left(x+1\right)}^2=-<!--\; -\; -->9$

Không có nghiệm thực vì bình phương của một số thực không bao giờ âm. Tuy nhiên, số phức có thể giải phương trình này bằng cách mở rộng trường số thực với đơn vị ảo $\mathrm{ı<!--\; ı\; -->}$, với ${\mathrm{ı<!--\; ı\; -->}}^2=-<!--\; -\; -->1$, giúp giải phương trình. Các nghiệm trong trường hợp này là −1 + 3i và −1 − 3i, và có thể xác nhận bằng cách thay vào phương trình với ${\mathrm{ı<!--\; ı\; -->}}^2=-<!--\; -\; -->1$:

Thực tế, không chỉ các phương trình bậc hai mà tất cả các phương trình đại số với hệ số thực hoặc số ảo đều có thể giải bằng số phức.

Định nghĩa

Số phức có thể được viết dưới dạng $a+b\mathrm{ı<!--\; ı\; -->}$, trong đó a và b là các số thực, và $i$ là đơn vị ảo, thỏa mãn điều kiện ${\mathrm{ı<!--\; ı\; -->}}^2=-<!--\; -\; -->1$. Ví dụ, $-<!--\; -\; -->3,5+2\mathrm{ı<!--\; ı\; -->}$ là một số phức.

Số thực a được gọi là phần thực của số phức $a+b\mathrm{ı<!--\; ı\; -->}$; số thực b là phần ảo của số phức $a+b\mathrm{ı<!--\; ı\; -->}$. Trong đó, phần ảo không bao gồm đơn vị ảo, do vậy b chứ không phải bi là phần ảo. Phần thực của số phức z được ký hiệu là Re(z) hoặc ℜ(z); phần ảo của số phức z được ký hiệu là Im(z) hoặc ℑ(z). Ví dụ:

Do đó, khi phân tích theo phần thực và phần ảo, một số phức z có thể viết dưới dạng $\mathrm{Re}<!--\; \; -->\left(z\right)+\mathrm{Im}<!--\; \; -->\left(z\right)\cdot <!--\; \cdot \; -->i$. Biểu thức này được gọi là dạng Cartesi của số phức z.

Một số thực a có thể được viết dưới dạng số phức là $a+0\mathrm{ı<!--\; ı\; -->}$ với phần ảo bằng 0. Số thuần ảo $b\mathrm{ı<!--\; ı\; -->}$ là số phức có dạng $0+b\mathrm{ı<!--\; ı\; -->}$ với phần thực bằng 0. Ngoài ra, khi phần ảo âm, nó được viết dưới dạng $a-<!--\; -\; -->b\mathrm{ı<!--\; ı\; -->}$ với $b>0$ thay vì $a+(-<!--\; -\; -->b)\mathrm{ı<!--\; ı\; -->}$, ví dụ $3-<!--\; -\; -->4\mathrm{ı<!--\; ı\; -->}$ thay vì $3+(-<!--\; -\; -->\; <div\; class="min-w-[250px]\; max-w-[94vw]\; md:max-w-[770px]">\; <ins\; class="adsbygoogle"\; style="display:block;\; text-align:center;"\; data-ad-layout="in-article"\; data-ad-format="fluid"\; data-ad-client="ca-pub-9247024304160346"\; data-ad-slot="4115752014"></ins>\; </div>4)\mathrm{ı<!--\; ı\; -->}$.

Tập hợp các số phức, hay còn gọi là trường số phức, được ký hiệu là ℂ, $C$ hoặc $C$. Có nhiều cách tiếp cận để xây dựng trường số phức một cách chặt chẽ thông qua các phương pháp tiên đề.

Gọi $R$ là tập hợp các số thực. Tập hợp các số phức được ký hiệu là $C$, bao gồm các cặp (a,b) với $a,b\in <!--\; \in \; -->R$.

Trong $C$, hai phép toán cơ bản được định nghĩa như sau:

$(a,b)+(c,d)=(a+c,b+d)$

$(a,b)\ast <!--\; \ast \; -->(c,d)=(ac-<!--\; -\; -->bd,ad+bc)$

Như vậy, $C$ là một trường số học (tham khảo cấu trúc đại số).

Có thể tạo một ánh xạ từ tập hợp số thực $R$ vào $C$ bằng cách gán mỗi số thực a với cặp $(a,0)\in <!--\; \in \; -->C$. Ví dụ: $0\to <!--\; \to \; -->(0,0),1\to <!--\; \to \; -->(1,0),-<!--\; -\; -->1\to <!--\; \to \; -->(-<!--\; -\; -->1,0)$... Qua phép ánh xạ này, tập các số thực $R$ được xem là tập con của tập các số phức $C$ và $C$ được coi là sự mở rộng của $R$.

Ký hiệu $\mathrm{ı<!--\; ı\; -->}$ đại diện cho cặp (0,1) thuộc $\in <!--\; \in \; -->C$. Chúng ta có

${\mathrm{ı<!--\; ı\; -->}}^2=(0,1)\times <!--\; \times \; -->(0,1)=(-<!--\; -\; -->1,0)=-<!--\; -\; -->1$.

Tất cả các số phức có dạng $b\mathrm{ı<!--\; ı\; -->}$ được gọi là số thuần ảo.

Các khái niệm quan trọng trong trường số phức

Biểu diễn đại số của số phức

Trong trường số phức, đơn vị ảo $\mathrm{ı<!--\; ı\; -->}$ có những đặc điểm được xác định bởi biểu thức

$i^2=-<!--\; -\; -->1$

$i=\sqrt{-<!--\; -\; -->1}$

Mỗi số phức z có thể được biểu diễn một cách duy nhất dưới dạng:

$z=a+bi$

trong đó a, b là các số thực. Đây là cách biểu diễn gọi là dạng đại số của số phức z.

Khi biểu diễn số phức dưới dạng đại số, các phép toán cộng và nhân thực hiện tương tự như phép cộng và nhân các nhị thức bậc nhất, với điều kiện rằng $i^2=-<!--\; -\; -->1$. Do đó, ta có các quy tắc sau:

$(a+ib)+(c+id)=(a+c)+i(b+d)$

$(a+ib)-<!--\; -\; -->(c+id)=(a-<!--\; -\; -->c)+i(b-<!--\; -\; -->d)$

$(a+bi)(c+di)=(ac-<!--\; -\; -->bd)+i(ad+bc)$

Mặt phẳng số phức

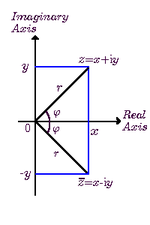
Trong hệ tọa độ Descartes, có thể dùng trục hoành để biểu diễn phần thực và trục tung để biểu diễn phần ảo của một số phức.

$z=x+iy.$

Mặt phẳng tọa độ lúc đó được gọi là mặt phẳng phức.

Số thực và số thuần ảo

Mỗi số thực $a$ được coi là một số phức với b = 0 {\displaystyle b=0} .

Ta có: $R$$\subset <!--\; \subset \; -->$$C$

Nếu a = 0 {\displaystyle a=0} , thì số phức $bi$ được gọi là thuần ảo.

Số phức liên hợp

Xét số phức dưới dạng đại số $Z=a+bi$, thì số phức $\stackrel{¯<!--\; ¯\; -->}{Z}=a-<!--\; -\; -->bi$ được gọi là số phức liên hợp của z.

Các đặc điểm của số phức liên hợp bao gồm:

1. $Z\times <!--\; \times \; -->\stackrel{¯<!--\; ¯\; -->}{Z}=a^2+b^2$ là một số thực.
2. $Z+\stackrel{¯<!--\; ¯\; -->}{Z}=2a$ là một số thực
3. $\stackrel{¯<!--\; ¯\; -->}{Z+Z^{\prime }}$ =$\stackrel{¯<!--\; ¯\; -->}{Z}+\stackrel{¯<!--\; ¯\; -->}{Z^{\prime }}$
4. $\stackrel{¯<!--\; ¯\; -->}{Z\times <!--\; \times \; -->Z^{\prime }}$ =$\stackrel{¯<!--\; ¯\; -->}{Z}\times <!--\; \times \; -->\stackrel{¯<!--\; ¯\; -->}{Z^{\prime }}$

Module và Argument

• Xét số phức $z=a+bi$. Khi đó, sản phẩm $z\times <!--\; \times \; -->\stackrel{¯<!--\; ¯\; -->}{z}=a^2+b^2$ chính là căn bậc hai của số phức $z\times <!--\; \times \; -->\stackrel{¯<!--\; ¯\; -->}{z}$, được gọi là module của số phức z, ký hiệu là $|z|$. Vì thế, ta có $|z|=\sqrt{a^2+b^2}$.

• Ta có thể biểu diễn số phức $z=a+bi$ trên mặt phẳng tọa độ với điểm $M(a,b)$, với góc $\mathrm{\phi <!--\; \phi \; -->}$ tạo bởi trục Ox dương và vectơ $\stackrel{\to <!--\; \to \; -->}{OM}$ được gọi là $argument$ của số phức $z$, ký hiệu là $arg\left(z\right)$.

Dạng lượng giác của số phức

Định nghĩa

Số phức $z=a+bi$ có thể được biểu diễn dưới dạng

Khi ta chọn

,

ta có thể viết số phức dưới dạng

Dạng biểu diễn này được gọi là dạng lượng giác của số phức $z$.

Các phép toán trên số phức ở dạng lượng giác

• Nhân và chia số phức khi ở dạng lượng giác

Xét hai số phức trong dạng lượng giác

Dạng biểu diễn này gọi là dạng lượng giác của số phức $z$.

Thực hiện lũy thừa tự nhiên của số phức trong dạng lượng giác (theo công thức Moirve).

• Tìm căn bậc n của số phức dưới dạng lượng giác.

Mỗi số phức khác 0 đều có đúng n căn bậc n, được biểu diễn dưới dạng

${\mathrm{\omega <!--\; \omega \; -->}}_k=\sqrt[n]{r}\left(\cos <!--\; \; -->{\mathrm{\psi <!--\; \psi \; -->}}_k+i\sin <!--\; \; -->{\mathrm{\psi <!--\; \psi \; -->}}_k\right)$

trong đó , $k=0,1,...n-<!--\; -\; -->1$

Các ứng dụng nổi bật

• Ứng dụng của số phức trong hình học phẳng: phép quay 90 độ tương đương với việc nhân với -1. Khi thực hiện hai phép quay 90 độ liên tiếp, chúng ta sẽ tương đương với phép quay 180 độ, tức là đảo ngược điểm gốc, tương đương với việc nhân với -1. Do đó, số ảo $\mathrm{ı<!--\; ı\; -->}$ biểu thị sự quay 90 độ. Chính vì $\mathrm{ı<!--\; ı\; -->}$ là đại diện cho phép quay 90 độ' nên số phức rất hữu ích trong hình học phẳng và lượng giác. Nhiều bài toán trong hình học phẳng hoặc công thức lượng giác phức tạp có thể trở nên dễ dàng hơn khi sử dụng số phức.
• Phân tích đa thức thành nhân tử.
• Tính toán các tích phân.
• Xác định dạng chuẩn và phân loại các cấu trúc toán học.
• Số phức xuất hiện nhiều trong vật lý hiện đại. Vì vật lý liên quan đến hình học và nhiều đại lượng có cả độ lớn lẫn hướng. Số phức rất phù hợp để mô tả các hiện tượng này, chẳng hạn như dòng điện xoay chiều, vì số ảo thể hiện phép quay 90 độ.

Các tập hợp số

$N$: Tập hợp các số tự nhiên

$Z$: Tập hợp các số nguyên

$Q$: Tập hợp các số hữu tỉ

$I=R\setminus <!--\; \setminus \; -->Q$: Tập hợp các số vô tỉ

$R$: Tập hợp các số thực

$C$: Tập hợp các số phức