Số thập phân là một khái niệm quan trọng trong toán học, dùng để biểu diễn và thực hiện các phép toán với các giá trị không phải nguyên. Trong bài viết này, chúng ta sẽ tìm hiểu về khái niệm này cũng như thực hành các bài toán để củng cố kiến thức.
Phân số thập phân là gì?
Phân số thập phân, hay còn gọi là số hệ thập phân, là một dạng phân số trong đó mẫu số là một bội số của 10 (ví dụ như 10, 100, 1000,…). Điều này cho phép biểu diễn phân số dưới dạng số hệ thập phân. Ví dụ, 1/10 có thể được biểu diễn là 0.1, 3/100 là 0.03. Tuy nhiên, nếu mẫu số không phải là bội số của 10, ví dụ như 1/3, thì không thể biểu diễn chính xác dưới dạng số hệ thập phân mà cần sử dụng các chữ số lặp lại hoặc làm tròn.
Dạng bài tập
Bài tập về số thập phân yêu cầu hiểu biết sâu về cơ chế hoạt động của số hệ thập phân và kỹ năng thực hiện các phép toán liên quan. Trong nhóm bài tập này, chúng ta sẽ tập trung vào các khía cạnh cơ bản của số hệ thập phân, bao gồm cả cách biểu diễn số hệ thập phân, phép cộng, trừ, nhân, chia, và các vấn đề liên quan đến chuyển đổi giữa số hệ thập phân và các hệ số khác nhau.
Dạng 1: Đọc các phân số thập phân
Bài tập: Đọc các phân số thập phân sau:
a) 25/10
b) 75/100
c) 6/10
d) 125/1000
e) 3/100
f) 23/10
g) 45/1000
h) 33/10

Giải đáp:
a) 25/10 được đọc là “hai mươi lăm phần mười”
b) 75/100 đọc là “bảy mươi lăm phần một trăm”
c) 6/10 đọc là “sáu phần mười”
d) 125/1000 đọc là “một trăm hai mươi lăm phần một nghìn”
e) 3/100 đọc là “ba phần một trăm”
f) 23/10 đọc là “hai mươi ba phần mười”
g) 45/1000 đọc là “bốn mươi lăm phần một nghìn”
h) 33/10 đọc là “ba mươi ba phần mười”
Dạng 2: Viết các số thập phân
Bài tập 1: Viết các số thập phân sau dưới dạng phân số:
a) 0.4
b) 0.9
c) 0.125
d) 0.75
Lời giải:
a) 0.4 viết dưới dạng phân số là 4/10
b) 0.9 viết dưới dạng phân số là 9/10
c) 0.125 viết dưới dạng phân số là 125/1000
d) 0.75 viết dưới dạng phân số là 75/100
Bài tập 2: Viết các số thập phân sau thành phân số:
a) Ba mươi hai phần một trăm
b) Năm phần một nghìn
c) Bảy mươi hai phần mười nghìn
d) Tám phần mười
Giải đáp:
a) Ba mươi hai phần một trăm: 32/100
b) Năm phần một nghìn: 5/1000
c) Bảy mươi hai phần mười nghìn: 72/10000
d) Tám phần mười: 8/10
Dạng 3: Viết các số phân số thành số thập phân
Bài tập: Viết các số phân số sau thành số thập phân:
a) Ba phần năm
b) Một phần hai
c) Bảy phần tám
d) Hai phần ba

Lời giải:
a) Ba phần năm = 0.6 = 6/10
b) Một phần hai = 0.5 = 5/10
c) Bảy phần tám = 0.875 = 875/1000
d) Hai phần ba = 0.66666 (hoặc làm tròn thành 0.67) = 67/100
Dạng 4: So sánh hai số thập phân
Bài tập: So sánh hai số hệ thập phân sau:
a) 0.25 và 0.3
b) 0.8 và 0.75
c) 0.125 và 0.15
d) 0.5 và 0.5

Lời giải:
a) 0.25 và 0.3
Chuyển thành phân số cùng mẫu số ta có 25/100 và 30/100. So sánh tử số ta được 25 < 30
Kết luận: 0.25 < 0.3
b) 0.8 và 0.75
Chuyển thành phân số cùng mẫu số ta có 80/100 và 75/100. So sánh tử số ta được 80 > 75
Kết luận: 0.8 > 0.75
c) 0.125 và 0.15
Đầu tiên chuyển thành phân số cùng mẫu số ta được 125/1000 và 150/1000. So sánh tử số ta được 125 < 150
Kết luận: 0.125 < 0.15
d) 0.5 và 0.5
Đầu tiên chuyển thành phân số cùng mẫu số ta được 5/10 và 5/10. So sánh tử số ta được 5 = 5
Kết luận: 0.5 = 0.5
Dạng 5: Phép cộng trừ các phân số hệ thập phân
Bài tập 1: Tính tổng của các phân số hệ thập phân sau:
a) 0.25 + 0.4
b) 0.8 + 0.35
c) 0.125 + 0.05
d) 0.6 + 0.75
e) 0.1 + 0.2
f) 0.35 + 0.45
g) 0.6 + 0.15
h) 0.9 + 0.05
Hướng dẫn: Để thực hiện phép cộng các số thập phân với nhau, ta lấy phần nguyên cộng phần nguyên và phần thập phân cộng với phần thập phân tương ứng.
Lời giải:
a) 0.25 + 0.4 = 0.65
b) 0.8 + 0.35 = 1.15
c) 0.125 + 0.05 = 0.175
d) 0.6 + 0.75 = 1.35
e) 0.1 + 0.2 = 0.3
f) 0.35 + 0.45 = 0.8
g) 0.6 + 0.15 = 0.75
h) 0.9 + 0.05 = 0.95
Bài tập 2: Tính hiệu của các phân số hệ thập phân sau:
a) 0.6 – 0.25 = 0.35
b) 0.8 – 0.35 = 0.45
c) 0.125 – 0.05 = 0.075
d) 0.9 – 0.75 = 0.15
e) 0.4 – 0.2 = 0.2
f) 0.35 – 0.15 = 0.2
g) 0.6 – 0.3 = 0.3
h) 0.9 – 0.05 = 0.85
Hướng dẫn: Để thực hiện phép trừ các số hệ thập phân với nhau, lấy phần nguyên trừ phần nguyên và lấy phần thập phân trừ phần thập phân.
Lời giải:
a) 0.6 – 0.25 = 0.35
b) 0.8 – 0.35 = 0.45
c) 0.125 – 0.05 = 0.075
d) 0.9 – 0.75 = 0.15
e) 0.4 – 0.2 = 0.2
f) 0.35 – 0.15 = 0.2
g) 0.6 – 0.3 = 0.3
h) 0.9 – 0.05 = 0.85
Dạng 6: Phép nhân các phân số thập phân
Nhân hai số hệ thập phân với nhau
Các bước thực hiện: Để nhân hai số hệ thập phân với nhau, ta có thể áp dụng các bước sau:
Bước 1: Bắt đầu với việc đặt phép tính, với số hệ thập phân thứ nhất là số hàng đơn vị và số hệ thập phân thứ hai là số hàng chục hoặc bất kỳ hàng nào khác tùy thuộc vào số lượng chữ số phần thập phân của từng số.
Bước 2: Thực hiện phép nhân giống như nhân hai số tự nhiên. Ta nhân từng chữ số của số thứ nhất với từng chữ số của số thứ hai, bắt đầu từ phải qua trái. Khi nhân, lưu ý rằng các chữ số phần thập phân của kết quả sẽ được xác định sau này.
Bước 3: Sau khi nhân, ta có tổng các tích của các chữ số. Để xác định vị trí dấu phẩy trong kết quả, sử dụng số lượng chữ số phần thập phân của từng thừa số. Vị trí dấu phẩy trong kết quả nằm ở vị trí mà tổng số chữ số phần thập phân của cả hai thừa số đã biết, tính từ phải qua trái.

Chỉ cần làm ba bước trên, ta có thể nhân hai số thập phân với nhau một cách chính xác. Cần lưu ý đặt đúng vị trí dấu phẩy và tính toán chính xác các chữ số phần thập phân của kết quả.
Bài toán ví dụ: 3,4 x 1,2
3,4
x
1,2
—
68
+
34
—
4,08
Vậy: 3,4 x 1,2 = 4,08

Nhân một số thập phân với 0,1; 0,01; 0,001; 0,0001
Khi nhân một số hệ thập phân bất kỳ với các số sau gồm 0,1; 0,01; 0,001; 0,0001;… ta có thể áp dụng quy tắc đơn giản là dịch dấu phẩy của số hệ thập phân ban đầu chuyển sang bên trái, tương ứng với số lượng chữ số sau dấu phẩy của số đó. Để thực hiện việc này, ta sẽ xem xét số hệ thập phân và xác định số lượng chữ số phần thập phân của nó. Sau đó, ta dịch dấu phẩy sang bên trái một, hai, ba, bốn,… chữ số tương ứng với số lượng chữ số phần thập phân của số đó.
Ví dụ 1, nếu ta có số thập phân 2,345 và muốn nhân nó với 0,01, ta thấy rằng số 0,01 này có hai chữ số phần thập phân. Do đó, ta sẽ dịch dấu phẩy của số 2,345 sang bên trái hai chữ số, và kết quả sẽ là 0,02345.
Ví dụ 2, tương tự, nếu ta có số hệ thập phân 7,89 và muốn nhân nó với 0,001, ta thấy rằng số 0,001 này có ba chữ số phần thập phân. Vì vậy, ta sẽ dịch dấu phẩy sang bên trái ba chữ số, và kết quả sẽ là 0,00789.

Quy tắc này giúp đơn giản hóa quá trình nhân số hệ thập phân với các số như 0,1; 0,01; 0,001; 0,0001;… giúp tiết kiệm thời gian và cũng giảm thiểu lỗi trong quá trình tính toán.
Nhân một số thập phân với một số tự nhiên
Các bước thực hiện: Khi muốn nhân một số hệ thập phân với một số tự nhiên, ta có thể áp dụng quy tắc sau:
Bước 1: Ta bắt đầu bằng việc nhân các chữ số của số tự nhiên với từng chữ số của số hệ thập phân, bắt đầu từ phải sang trái. Tương tự như quy tắc nhân thông thường, ta nhân từng cặp chữ số và ghi kết quả tạm thời.
Bước 2: Sau khi thực hiện phép nhân, ta xem xét phần thập phân của số hệ thập phân và đếm số chữ số trong phần đó. Số lượng chữ số này sẽ xác định vị trí dấu phẩy trong kết quả. Ta sẽ đặt dấu phẩy tách các chữ số trong tích, bắt đầu từ phải sang trái, tương ứng với số lượng chữ số trong phần thập phân.
Bài toán ví dụ: 3,18 x 4
3,18
x
4
——
12,72
Vậy: 3,18 x 4 = 12,72
Nhân một số thập phân với 10, 100, 1000,…
Khi muốn nhân một số hệ thập phân bất kỳ với các số 10, 100, 1000,… ta có thể áp dụng quy tắc đơn giản là chuyển dấu phẩy của số đó sang bên phải một, hai, ba, … chữ số. Để thực hiện việc này, ta chỉ cần xem xét số hệ thập phân và xác định số lượng chữ số phần thập phân của nó. Tiếp theo, ta sẽ chuyển dấu phẩy sang bên phải một số lượng chữ số tương ứng với số lượng chữ số phần thập phân của số đó.
Ví dụ 1, nếu ta có số hệ thập phân 2,345 và muốn nhân nó với 10, ta thấy rằng số 10 có có một số 0. Để nhân với 10, ta chỉ cần chuyển dấu phẩy sang bên phải một chữ số, và kết quả sẽ là 23,45.
Ví dụ 2, tương tự, nếu ta có số hệ thập phân 7,89 và muốn nhân nó với 100, ta thấy rằng số 100 có hai số 0. Vì vậy, ta sẽ chuyển dấu phẩy sang bên phải hai chữ số, và kết quả sẽ là 789.

Quy tắc này giúp ta có được kết quả phép tính nhân một số hệ thập phân với 10, 100, 1000,… một cách nhanh chóng. Chỉ cần chuyển dấu phẩy sang bên phải một số lượng chữ số tương ứng với số lượng chữ số phần thập phân của số hệ thập phân ban đầu. Điều này giúp ta tiết kiệm thời gian và giảm thiểu lỗi trong quá trình tính toán.
Dạng 7: Phép chia các phân số thập phân
Chia một số hệ thập phân cho một số hệ thập phân
Các bước thực hiện: Khi muốn chia một số hệ thập phân cho một số hệ thập phân, ta có thể áp dụng quy tắc sau:
Bước 1: Ta xem xét số chia và đếm số lượng chữ số trong phần thập phân của nó. Số lượng chữ số này sẽ xác định số lượng chữ số phần thập phân của kết quả.
Bước 2: Sau khi xác định số lượng chữ số phần thập phân của số chia, ta sẽ chuyển dấu phẩy của số bị chia sang bên phải một số lượng chữ số tương ứng. Điều này tương đương với việc bỏ dấu phẩy của số bị chia.
Bước 3: Sau khi bỏ dấu phẩy của số bị chia, ta tiến hành phép chia giống như khi chia số tự nhiên. Ta thực hiện phép chia và ghi kết quả tạm thời.
Bài toán ví dụ: Ví dụ: 13,11 : 2,3
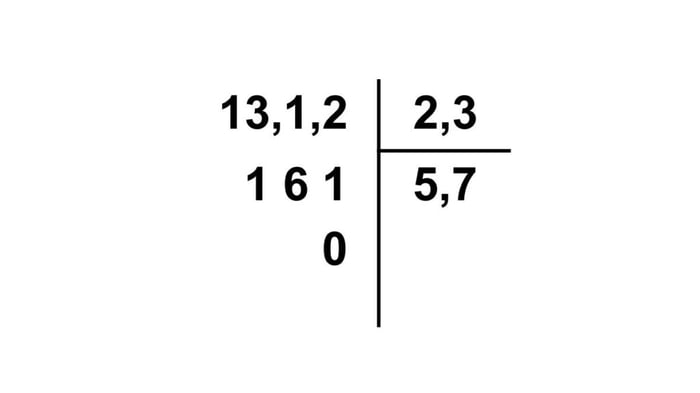
- Ta có phần thập phân của số 2,3 có một chữ số
- Dịch chuyển dấu phẩy của số 13,11 sang bên phải một chữ số ta được 131,1 và bỏ một dấu phẩy ở số 2,3 ta được số 23
- Sau đó ta tiến hành phép chia 131,1 : 23 bình thường
Chia một số thập phân cho một số tự nhiên
Các bước thực hiện: Khi muốn chia một số hệ thập phân cho một số tự nhiên, ta có thể áp dụng quy tắc sau:
Bước 1: Bắt đầu bằng việc lấy phần nguyên của số bị chia và thực hiện phép chia với số chia như khi chia số tự nhiên. Kết quả của phép chia này là phần nguyên của kết quả cuối cùng.
Bước 2: Sau khi có phần nguyên của kết quả, đặt dấu phẩy vào bên phải thương đã tìm được. Tiếp theo, lấy chữ số đầu tiên ở phần thập phân của số bị chia và đặt nó vào sau dấu phẩy. Sử dụng chữ số này để tiếp tục thực hiện phép chia.
Bước 3: Tiếp tục chia từng chữ số tiếp theo ở phần thập phân của số bị chia như chia số tự nhiên. Kết quả từng phép chia sẽ là các chữ số tiếp theo của kết quả cuối cùng.
Bài toán ví dụ: 37,52 : 4
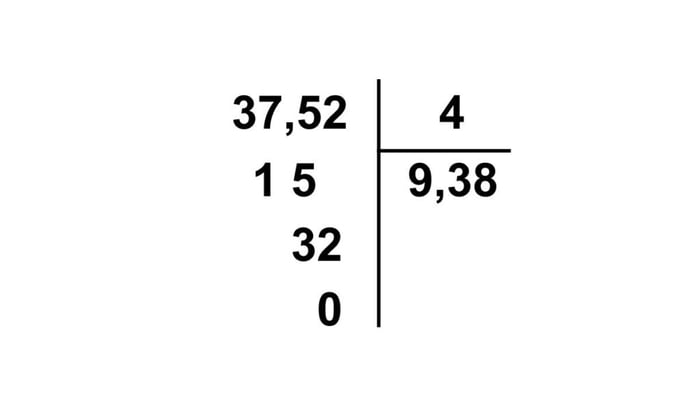
- Chia phần nguyên của 37 cho 4 được 9 và dư 1
- Viết dấu phẩy vào bên phải thương đã tìm được, ta có 9
- Hạ số tiếp theo sau dấu phẩy là số 5, ta có 15 chia cho 4 được 3 dư 3
- Hạ số tiếp theo của số bị chia xuống là số 2, ta có 32 chia cho 4 được 8 dư 0
- Kết hợp kết quả từ các phép chia trên, kết quả cuối cùng là 9,38
Chia một số tự nhiên cho một số thập phân
Các bước thực hiện: Khi muốn chia một số tự nhiên cho một số thập phân, ta có thể áp dụng quy tắc sau:
Bước 1: Xem xét số chia và đếm số lượng chữ số trong phần thập phân của nó. Số lượng chữ số này sẽ xác định số lượng chữ số phần thập phân của kết quả.
Bước 2: Sau khi xác định số lượng chữ số phần thập phân của số chia, viết thêm bấy nhiêu chữ số 0 vào bên phải số bị chia. Điều này tương đương với việc bỏ dấu phẩy của số chia.
Bước 3: Sau khi loại bỏ dấu phẩy của số bị chia, thực hiện phép chia giống như khi chia các số tự nhiên. Thực hiện phép chia và ghi lại kết quả tạm thời.
Bài toán ví dụ: 4:1,25
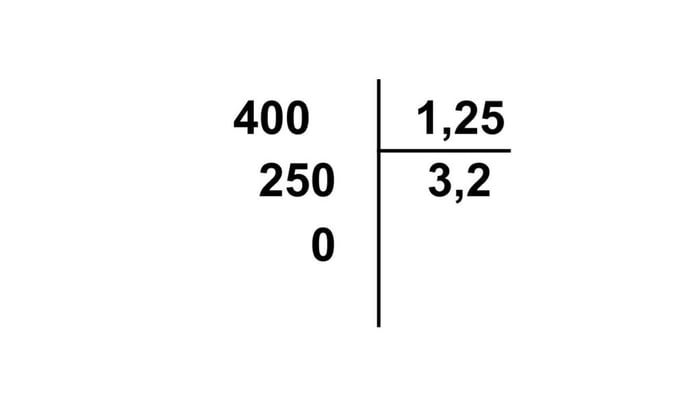
- Phần thập phân của số 1,25 có hai chữ số
- Thêm hai chữ số 0 vào bên phải số 4 để có số bị chia là 400 và loại bỏ dấu phẩy của số chia để có số 125
- Thực hiện phép chia như bình thường và được kết quả là 3,2
Tạm kết
Trong bài viết này của Mytour, chúng ta thấy sự liên quan chặt chẽ giữa số thập phân và các kiểu số khác, cung cấp cơ sở vững chắc để nắm bắt các khái niệm toán học phức tạp hơn. Các bài toán tính toán đã được tổng hợp trong bài viết này không chỉ là một phần quan trọng trong chương trình học mà còn là một kỹ năng quan trọng giúp chúng ta hiểu rõ hơn về thế giới xung quanh và làm chủ các khía cạnh khác nhau của cuộc sống liên quan đến đo đạc và tính toán.
