Sử dụng 'Các chỉ số Hy Lạp' để Hiểu về Lựa chọn

Cố gắng dự đoán những gì sẽ xảy ra với giá của một lựa chọn đơn lẻ hoặc một vị thế liên quan đến nhiều lựa chọn khi thị trường thay đổi có thể là một nhiệm vụ khó khăn. Bởi vì giá của lựa chọn không luôn luôn di chuyển cùng với giá của tài sản cơ bản, điều quan trọng là hiểu những yếu tố nào góp phần vào sự di chuyển của giá của một lựa chọn và tác động của chúng.

Các nhà giao dịch lựa chọn thường đề cập đến delta, gamma, vega và theta của vị thế lựa chọn của họ. Tổng thể, những thuật ngữ này được gọi là các Chỉ số Hy Lạp và chúng cung cấp một cách để đo lường độ nhạy cảm của giá của một lựa chọn đối với các yếu tố có thể định lượng được. Những thuật ngữ này có thể làm cho những nhà giao dịch lựa chọn mới cảm thấy rối bời và gây sợ hãi, nhưng khi phân rã, các Chỉ số Hy Lạp tham khảo đến những khái niệm đơn giản có thể giúp bạn hiểu rõ hơn về rủi ro và tiềm năng thu nhập từ vị thế lựa chọn.

Những điều quan trọng cần lưu ý

Tìm hiểu các Chỉ số Hy Lạp

Trước tiên, bạn nên hiểu rằng các con số cho mỗi chỉ số Hy Lạp là một lý thuyết nghiêm ngặt. Điều đó có nghĩa là các giá trị được dự đoán dựa trên các mô hình toán học. Hầu hết thông tin bạn cần để giao dịch tùy chọn—như giá đề nghị, giá yêu cầu và giá cuối cùng, khối lượng và lợi nhuận mở—đều là dữ liệu thực tế nhận được từ các sàn giao dịch tùy chọn khác nhau và được phân phối bởi dịch vụ dữ liệu và/hoặc công ty môi giới của bạn.

Các chỉ số Hy Lạp cần được tính toán và độ chính xác của chúng chỉ tốt như mô hình được sử dụng để tính toán chúng. Để có được chúng, bạn cần truy cập vào một giải pháp máy tính hóa tính chúng cho bạn. Hầu hết các công ty môi giới bán lẻ (như interactive brokers) cũng cung cấp thông tin này. Tất nhiên, bạn có thể học toán học và tính toán các chỉ số Hy Lạp bằng tay cho từng tùy chọn, nhưng với số lượng lớn các tùy chọn có sẵn và hạn chế thời gian, điều đó sẽ không thực tế.

Dưới đây là một ma trận cho thấy nhiều giá đề nghị của tùy chọn từ tháng 3, tháng 4 và tháng 5 năm 2018, cho một cổ phiếu hiện đang giao dịch ở mức $60. Nó được định dạng để hiển thị giá trung bình, delta, gamma, theta và vega cho mỗi tùy chọn. Khi chúng tôi thảo luận về ý nghĩa của mỗi chỉ số Hy Lạp, bạn có thể tham khảo hình minh họa này để giúp bạn hiểu rõ các khái niệm.

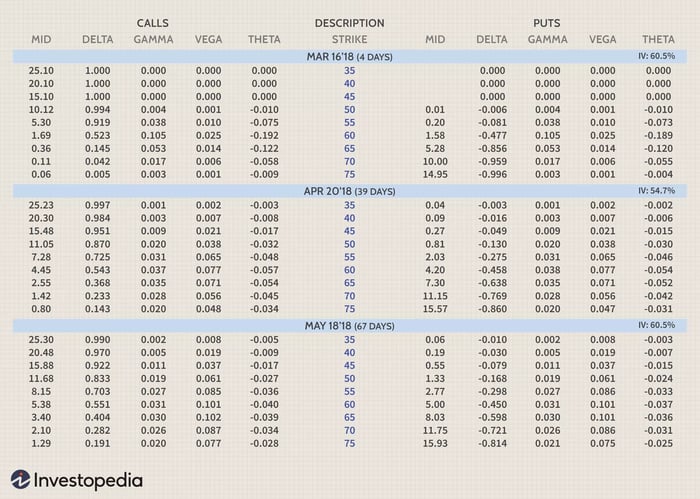
Phần bên trái hiển thị các tùy chọn mua (call options), trong khi phần bên phải hiển thị các tùy chọn bán (put options). Hãy chú ý rằng các giá đình (strike prices) được liệt kê dọc theo chiều dọc màu xanh giữa. Các tùy chọn ngoài tiền (out-of-the-money) là những tùy chọn có giá đình cao hơn 60 cho tùy chọn mua và giá đình thấp hơn 60 cho tùy chọn bán. Các tùy chọn trong tiền (in-the-money) có giá đình từ 60 và thấp hơn cho tùy chọn mua và từ 60 và cao hơn cho tùy chọn bán (cột được làm nổi bật màu xanh).

Khi bạn di chuyển từ trên xuống dưới, các ngày đáo hạn tăng từ tháng Ba đến tháng Tư và sau đó là tháng Năm. Số ngày còn lại cho đến ngày đáo hạn được hiển thị trong ngoặc đơn trong cột mô tả ở giữa ma trận. Đây là định dạng mà chúng tôi sử dụng trong lớp Học tùy chọn cho người mới bắt đầu tại Mytour Academy.

Các con số delta, gamma, theta và vega được hiển thị ở trên được chuẩn hóa theo đơn vị đô la. Để chuẩn hóa các chỉ số Hy Lạp theo đơn vị đô la, bạn đơn giản nhân chúng với bộ nhân hợp đồng của tùy chọn. Bộ nhân hợp đồng sẽ là 100 (cổ phiếu) cho hầu hết các tùy chọn cổ phiếu. Cách mà các chỉ số Hy Lạp khác nhau khi điều kiện thay đổi phụ thuộc vào khoảng cách giá đình so với giá thực của cổ phiếu và số ngày còn lại cho đến ngày đáo hạn.

Khi Giá Cổ Phiếu Cơ Bản Thay Đổi—Delta và Gamma

Đơn giản nhất, delta là số tiền dự kiến mà giá của tùy chọn sẽ di chuyển dựa trên mỗi thay đổi $1 của tài sản cơ bản. Delta do đó đo lường độ nhạy cảm của giá trị lý thuyết của tùy chọn đối với sự thay đổi trong giá của tài sản cơ bản. Thông thường, nó được biểu diễn dưới dạng một số từ âm một đến một và cho biết mức độ mà giá trị của tùy chọn sẽ thay đổi khi giá cổ phiếu cơ bản tăng lên một đô la.

Theo một cách hiệu lực khác, delta cũng có thể được hiển thị dưới dạng một giá trị từ -100 đến +100 để cho thấy độ nhạy cảm đô la tổng hợp đối với 1 tùy chọn, bao gồm 100 cổ phiếu cơ bản. Các delta được chuẩn hóa ở trên cho thấy số đô la thực tế mà bạn sẽ thu được hoặc mất. Ví dụ, nếu bạn sở hữu tùy chọn mua tháng 12 với giá đình -45.2, bạn sẽ mất $45.20 nếu giá cổ phiếu tăng lên một đô la.

Tùy chọn mua có delta dương và tùy chọn bán có delta âm. Tùy chọn ở tiền (at-the-money) nói chung có delta xung quanh 50. Tùy chọn sâu trong tiền (deep-in-the-money) có thể có delta 80 hoặc cao hơn, trong khi tùy chọn ngoài tiền (out-of-the-money) có delta nhỏ hơn hoặc bằng 20. Khi giá cổ phiếu di chuyển, delta sẽ thay đổi khi tùy chọn trở nên sâu vào hoặc ra khỏi tiền. Khi một tùy chọn cổ phiếu trở nên rất sâu trong tiền (delta gần 100), nó sẽ bắt đầu giao dịch giống như cổ phiếu, di chuyển gần như mỗi đô la với giá cổ phiếu. Trong khi đó, các tùy chọn rất ngoài tiền sẽ không di chuyển nhiều về mặt tuyệt đối đô la. Delta cũng là một con số rất quan trọng để xem xét khi xây dựng vị thế kết hợp.

Bởi vì delta là yếu tố quan trọng như vậy, các nhà giao dịch tùy chọn cũng quan tâm đến việc delta có thể thay đổi như thế nào khi giá cổ phiếu di chuyển. Gamma đo lường tỷ lệ thay đổi của delta cho mỗi tăng một điểm trong tài sản cơ bản. Đây là một công cụ quý giá giúp bạn dự đoán sự thay đổi của delta của một tùy chọn hoặc một vị thế tổng thể. Gamma sẽ lớn hơn cho các tùy chọn ở tiền và dần giảm đối với cả tùy chọn trong và ngoài tiền. Khác với delta, gamma luôn là dương cho cả tùy chọn mua và bán.

Biến động trong Biến động và Sự Trôi Dần của Thời Gian—Theta và Vega

Theta là một đơn vị đo lường sự suy giảm thời gian của một tùy chọn, số đô la mà một tùy chọn sẽ mất mỗi ngày do sự trôi dần của thời gian. Đối với các tùy chọn ở tiền (at-the-money), theta tăng khi tùy chọn đến gần ngày đáo hạn. Đối với các tùy chọn trong và ngoài tiền (in- and out-of-the-money), theta giảm khi tùy chọn đến gần ngày đáo hạn.

Theta là một trong những khái niệm quan trọng nhất mà một nhà giao dịch tùy chọn mới bắt đầu cần hiểu vì nó giải thích tác động của thời gian lên phần thưởng của các tùy chọn mua hoặc bán. Càng đi xa trong thời gian, sự suy giảm thời gian của một tùy chọn sẽ càng nhỏ. Nếu bạn muốn sở hữu một tùy chọn, thì mua các hợp đồng dài hạn là có lợi. Nếu bạn muốn một chiến lược thu lợi từ sự suy giảm thời gian, bạn sẽ muốn bán short các tùy chọn ngắn hạn để giảm giá trị nhanh chóng do thời gian.

Greek cuối cùng chúng ta sẽ xem là vega. Nhiều người nhầm lẫn giữa vega và biến động. Biến động đo lường sự biến động của tài sản cơ bản. Vega đo lường độ nhạy cảm của giá của một tùy chọn đối với sự thay đổi trong biến động. Một sự thay đổi trong biến động sẽ ảnh hưởng đến cả tùy chọn mua và bán cùng một cách. Một tăng trong biến động sẽ làm tăng giá của tất cả các tùy chọn trên một tài sản, và một giảm trong biến động sẽ làm giảm giá trị của tất cả các tùy chọn.

Tuy nhiên, mỗi tùy chọn cá nhân đều có vega riêng và sẽ phản ứng với sự thay đổi biến động một cách khác nhau một chút. Tác động của sự thay đổi biến động lớn hơn đối với các tùy chọn ở tiền so với các tùy chọn trong hoặc ngoài tiền. Các nhà giao dịch có thể làm giảm tác động của rủi ro biến động ngụ ý bằng cách sử dụng chiến lược vega trung lập.

Mặc dù vega ảnh hưởng đến cả tùy chọn mua và bán một cách tương tự, nhưng có vẻ như nó ảnh hưởng đến tùy chọn mua nhiều hơn tùy chọn bán. Có lẽ do sự mong đợi về sự phát triển của thị trường theo thời gian, hiệu ứng này rõ ràng hơn đối với các tùy chọn dài hạn như LEAPS.

Sử dụng các Greek để Hiểu các Giao dịch Kết hợp

Ngoài việc sử dụng các Greek trên từng tùy chọn cá nhân, bạn cũng có thể áp dụng chúng cho các vị thế kết hợp nhiều tùy chọn. Điều này có thể giúp bạn định lượng các rủi ro khác nhau của mỗi giao dịch mà bạn cân nhắc, dù cho có phức tạp đến đâu. Vì các vị thế tùy chọn có nhiều mức độ tiếp xúc với rủi ro, và những rủi ro này thay đổi mạnh mẽ theo thời gian và với sự di chuyển của thị trường, vì vậy việc hiểu chúng một cách dễ dàng là rất quan trọng.

Dưới đây là một đồ thị rủi ro cho thấy lợi/lỗ có thể của một spread gọi dọc (vertical call debit spread) kết hợp 10 tùy chọn mua tháng 5 với giá 60 và bán 10 tùy chọn mua tháng 5 với giá 65. Trục ngang hiển thị giá cổ phiếu XYZ Corp từ thấp đến cao từ trái sang phải, trong khi trục đứng hiển thị lợi/lỗ của vị thế. Cổ phiếu hiện đang giao dịch tại $60.22.

Đường chấm chỉ ra lợi/lỗ của vị thế spread qua tháng 5 cùng với đường đặc chỉ ra lợi/lỗ cho ngày hôm nay. Rõ ràng, đây là một vị thế lạc quan (thực tế là thường được gọi là bull call spread) và chỉ được đặt nếu bạn dự đoán cổ phiếu sẽ tăng giá.

Các chỉ số Greeks giúp bạn nhìn thấy mức độ nhạy cảm của vị thế đối với sự thay đổi trong giá cổ phiếu, biến động và thời gian. Phần kịch bản có sự thay đổi 10% trong giá cổ phiếu cơ bản. Bảng trên cho thấy lợi/lỗ dự đoán, delta, gamma, theta, và vega cho vị thế sẽ là vào ngày 16 tháng 5 năm 2018. Có vẻ phức tạp, nhưng nếu bạn muốn học cách đơn giản hóa cách nghĩ về các Greek, bạn có thể tham gia khóa Học tập Tùy chọn cho Người mới bắt đầu của Mytour, nơi cố gắng phân tích những khái niệm này thành các khái niệm dễ tiếp thu.

Các Greek Nhỏ

Ngoài các yếu tố rủi ro được liệt kê ở trên, các nhà giao dịch tùy chọn cũng có thể tìm đến đạo hàm cấp hai và ba để chỉ ra sự thay đổi trong những yếu tố rủi ro đó khi có sự thay đổi trong các biến số khác. Mặc dù ít được sử dụng hơn, chúng vẫn hữu ích để hiểu rõ hơn về hồ sơ rủi ro hoàn chỉnh của một vị thế tùy chọn.

Một số Greek nhỏ này bao gồm lambda, epsilon, vomma, vera, speed, zomma, color, và ultima.

Các Greek này ảnh hưởng đến những thay đổi như sự thay đổi của delta khi có biến động trong biến động và như vậy. Mặc dù ít được biết đến hơn, chúng ngày càng được sử dụng nhiều trong các chiến lược giao dịch tùy chọn khi phần mềm máy tính có thể nhanh chóng tính toán và tính đến những yếu tố rủi ro phức tạp và đôi khi khó hiểu này.

Bài học quan trọng

Các chỉ số Hy Lạp giúp xác định các rủi ro và tiềm năng lợi nhuận của một vị thế tùy chọn. Sau khi bạn hiểu rõ những cơ bản này, bạn có thể áp dụng vào chiến lược hiện tại của mình. Việc chỉ biết vốn rủi ro toàn bộ trong một vị thế tùy chọn không đủ. Để hiểu được khả năng một giao dịch có thể mang lại lợi nhuận, việc xác định các chỉ số đo lường rủi ro là rất quan trọng.

Khi điều kiện thị trường thay đổi liên tục, các chỉ số Hy Lạp cung cấp cho nhà giao dịch cách xác định mức độ nhạy cảm của một giao dịch cụ thể đối với biến động giá, biến động biến động và thời gian. Kết hợp hiểu biết về các chỉ số Hy Lạp với các đồ thị rủi ro mạnh mẽ có thể nâng cao giao dịch tùy chọn của bạn lên một tầm cao mới.