Sự phản ánh

Trong lĩnh vực toán học, sự phản ánh (tiếng Anh: mapping) là khái niệm mô tả một quan hệ giữa hai tập hợp, kết nối mỗi phần tử của tập hợp đầu tiên (gọi là tập nguồn) với đúng một phần tử của tập hợp thứ hai (gọi là tập đích). Tập nguồn và tập đích không nhất thiết phải là tập số thực hay tập con của số thực mà có thể là tập hợp của các vector, hàm phân tích, biến ngẫu nhiên, v.v. Nói cách khác, một sự phản ánh thể hiện một quy tắc hoặc thao tác toán học nhất định để chuyển đổi từ một phần tử trong một không gian (tập hợp) sang đúng một phần tử (thường gọi là hình ảnh) trong không gian (tập hợp) khác. Các sự phản ánh có thể là toàn ánh, đơn ánh hoặc song ánh tùy thuộc vào tính chất của hình ảnh trong tập hợp thứ hai, và có thể được biểu diễn qua các toán tử, ký hiệu toán học hoặc phép toán từ cơ bản đến nâng cao. Ví dụ, phép biến đổi Laplace là một sự phản ánh từ tập chứa các hàm trong miền thời gian sang tập chứa các hàm trong miền tần số phức thông qua một phép biến đổi tích phân. Hay một ma trận thường được dùng để biểu diễn sự phản ánh tuyến tính giữa hai không gian Euclide.

Khi hai tập hợp là tập số thực hoặc tập con của số thực, sự phản ánh giữa chúng thường được gọi là hàm số. Điều này có nghĩa là hàm số được xem như một trường hợp đặc biệt của sự phản ánh.

Định nghĩa trong toán học

Một ánh xạ f từ tập hợp X đến tập hợp Y (ký hiệu $f:X\to <!--\; \to \; -->Y$) là một quy tắc ánh xạ mỗi phần tử x $\in <!--\; \in \; -->$ X đến một phần tử y $\in <!--\; \in \; -->$ Y, trong đó y là hình ảnh của x, ký hiệu là $y=f\left(x\right)$, nghĩa là $\mathrm{\forall <!--\; \forall \; -->}x\in <!--\; \in \; -->X,\mathrm{\exists <!--\; \exists \; -->}!y\in <!--\; \in \; -->Y,y=f\left(x\right)$.

Tập hợp X gọi là tập nguồn và tập hợp Y gọi là tập đích.

Đối với mỗi $y\in <!--\; \in \; -->Y$, tập con của X chứa các phần tử có hình ảnh qua ánh xạ f bằng y, được gọi là hình ảnh ngược của phần tử y qua f, ký hiệu là $f^{-<!--\; -\; -->1}\left(y\right)$. Ta có$f^{-<!--\; -\; -->1}\left(y\right)=\{x\in <!--\; \in \; -->X|f(x)=y\}$.

Đối với mỗi tập con $A\subset <!--\; \subset \; -->X$, tập con của Y gồm các phần tử là hình ảnh của $x\in <!--\; \in \; -->A$ qua ánh xạ f gọi là hình ảnh của tập A, ký hiệu là f(A). Ta có$f\left(A\right)=\left\{f\right(x)|x\in <!--\; \in \; -->A\}$.

Đối với mỗi tập con $B\subset <!--\; \subset \; -->Y$, tập con của X chứa các phần tử x sao cho hình ảnh $f\left(x\right)\in <!--\; \in \; -->B$ được gọi là hình ảnh ngược của tập B, ký hiệu là $f^{-<!--\; -\; -->1}\left(B\right)$. Ta có$f^{-<!--\; -\; -->1}\left(B\right)=\{x\in <!--\; \in \; -->X|f(x)\in <!--\; \in \; -->B\}$.

Liên quan đến khái niệm về quan hệ, chúng ta có thể định nghĩa như sau:

Một ánh xạ $F$ từ tập X đến tập Y được gọi là một quan hệ $F$ giữa X và Y nếu mọi phần tử $x\in <!--\; \in \; -->X$ đều có liên kết với duy nhất một phần tử $y\in <!--\; \in \; -->Y$.

Những đặc điểm cơ bản

• Ảnh của một tập hợp rỗng luôn là tập hợp rỗng

$A=\mathrm{\varnothing <!--\; \varnothing \; -->}\iff <!--\; \iff \; -->f\left(A\right)=\mathrm{\varnothing <!--\; \varnothing \; -->}$

• Ảnh của một tập con sẽ luôn là một tập con của ảnh

$A\subset <!--\; \subset \; -->B$$\Rightarrow <!--\; \Rightarrow \; -->f\left(A\right)\subset <!--\; \subset \; -->f\left(B\right)$

• Ảnh của giao giữa hai tập con nằm trong giao của ảnh của chúng

$f(A\cap <!--\; \cap \; -->B)\subset <!--\; \subset \; -->f\left(A\right)\cap <!--\; \cap \; -->f\left(B\right)$

• Ảnh của hợp giữa hai tập con chính là hợp của các ảnh của chúng

$f(A\cup <!--\; \cup \; -->B)=f\left(A\right)\cup <!--\; \cup \; -->f\left(B\right)$

Toàn ánh, đơn ánh và song ánh

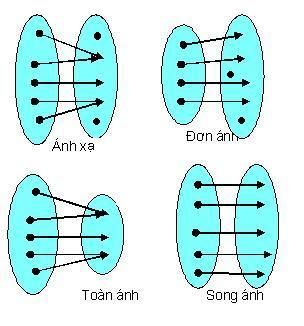
• Toàn ánh là ánh xạ từ X vào Y sao cho ảnh của X bao phủ toàn bộ Y. Trong trường hợp này, f còn được gọi là ánh xạ từ X lên Y

$f\left(\mathrm{X\; <div\; class="min-w-[250px]\; max-w-[94vw]\; md:max-w-[770px]">\; <ins\; class="adsbygoogle"\; style="display:block;\; text-align:center;"\; data-ad-layout="in-article"\; data-ad-format="fluid"\; data-ad-client="ca-pub-9247024304160346"\; data-ad-slot="4115752014"></ins>\; </div>}\right)=Y$

hoặc

$\mathrm{\forall <!--\; \forall \; -->}y\in <!--\; \in \; -->Y,\mathrm{\exists <!--\; \exists \; -->}x\in <!--\; \in \; -->X:f\left(x\right)=y$

• Đơn ánh là ánh xạ mà các phần tử khác nhau của X có các ảnh khác nhau trong Y. Đơn ánh cũng được gọi là ánh xạ 1-1 do tính chất này.

$\mathrm{\forall <!--\; \forall \; -->}{x}_1,x_2\in <!--\; \in \; -->X:x_1\ne <!--\; \ne \; -->x_2\Rightarrow <!--\; \Rightarrow \; -->f\left(x_1\right)\ne <!--\; \ne \; -->f\left(x_2\right)$

hoặc

$\mathrm{\forall <!--\; \forall \; -->}{x}_1,x_2\in <!--\; \in \; -->X:f\left(x_1\right)=f\left(x_2\right)\Rightarrow <!--\; \Rightarrow \; -->x_1=x_2$

• Song ánh là ánh xạ vừa đơn ánh vừa toàn ánh. Nó đồng thời là ánh xạ 1-1 và ánh xạ 'onto' (từ X lên Y).

Một số ánh xạ đặc biệt

• Ánh xạ hằng: Là ánh xạ từ X vào Y sao cho mỗi phần tử x $\in <!--\; \in \; -->$ X đều ánh xạ tới cùng một phần tử duy nhất $y_0$ $\in <!--\; \in \; -->$ Y.
• Ánh xạ đồng nhất: Là ánh xạ từ X vào chính X sao cho mọi phần tử x trong X đều thỏa mãn f(x)=x.
• Ánh xạ nhúng: Là ánh xạ f từ tập con $X\subset <!--\; \subset \; -->Y$ vào Y sao cho f(x) = x với mọi $x\in <!--\; \in \; -->X$ (còn được gọi là đơn ánh chính tắc). Ta ký hiệu f: X $\hookrightarrow <!--\; \hookrightarrow \; -->$ Y. Một cách hiểu khác về ánh xạ nhúng là: nếu $f:X\to <!--\; \to \; -->Y$ là đơn ánh, khi xem f như một ánh xạ từ X vào tập con $f\left(X\right)\subset <!--\; \subset \; -->Y$, thì f sẽ là song ánh. Khi đó, ta có sự tương ứng 1-1 giữa X với f(X) và có thể thay thế các phần tử của tập con $f\left(X\right)\subset <!--\; \subset \; -->Y$ bằng các phần tử của tập X. Đây gọi là việc nhúng X vào Y bằng ánh xạ đơn ánh f.

Các phép toán

Ánh xạ hợp nhất

Xét hai ánh xạ $f:X\to <!--\; \to \; -->Y$ và $g:Y\to <!--\; \to \; -->Z$. Ánh xạ hợp của f và g, ký hiệu $g\circ <!--\; \circ \; -->f$, là ánh xạ từ X đến Z, được xác định bởi đẳng thức $(g\circ <!--\; \circ \; -->f)\left(x\right)=g\left(f\right(x\left)\right)$ (hay còn gọi là tích ánh xạ của f và g).

Một số đặc điểm của ánh xạ hợp

• Nếu $(g\circ <!--\; \circ \; -->f)$ là đơn ánh thì f cũng phải là đơn ánh.
• Nếu $(g\circ <!--\; \circ \; -->f)$ là toàn ánh thì g cũng phải là toàn ánh.
• Nếu $(g\circ <!--\; \circ \; -->f)$ là song ánh thì cả f và g đều phải là song ánh.

Ánh xạ ngược

Xét ánh xạ $f:X\to <!--\; \to \; -->Y$ là song ánh. Nếu tồn tại ánh xạ $g:Y\to <!--\; \to \; -->X$ sao cho

$\mathrm{\forall <!--\; \forall \; -->}x\in <!--\; \in \; -->X:(g\circ <!--\; \circ \; -->f)\left(x\right)=x$

$\mathrm{\forall <!--\; \forall \; -->}y\in <!--\; \in \; -->Y:(f\circ <!--\; \circ \; -->g)\left(y\right)=y$

thì g được gọi là nghịch đảo, hay ánh xạ ngược, của f, và được ký hiệu là $f^{-<!--\; -\; -->1}$.

Ánh xạ f có nghịch đảo nếu và chỉ nếu f là song ánh.

Ánh xạ thu hẹp

Xét ánh xạ $f:X\to <!--\; \to \; -->Y$ và một tập con $E\subset <!--\; \subset \; -->X$. Ánh xạ thu hẹp của $f$ lên $E$ là một ánh xạ từ $E$ vào $Y$, được ký hiệu là $f{|}_E$, và được xác định bởi đẳng thức $f{|}_E\left(x\right)=f\left(x\right)$. Ánh xạ thu hẹp này là duy nhất.

Ánh xạ mở rộng

Xét ánh xạ $f:X\to <!--\; \to \; -->Y$ và một tập hợp $F$ sao cho $X\subset <!--\; \subset \; -->F$. Một ánh xạ mở rộng của $f$ lên $F$ là một ánh xạ $\stackrel{~<!--\; ~\; -->}{f}$ từ $F$ vào $Y$ sao cho $\mathrm{\forall <!--\; \forall \; -->}x\in <!--\; \in \; -->X:\stackrel{~<!--\; ~\; -->}{f}\left(x\right)=f\left(x\right)$. Thông thường, mỗi ánh xạ có thể được mở rộng theo nhiều cách khác nhau.

Các khái niệm ánh xạ khác (dịch từ tiếng Anh)

• Ánh xạ ảnh
• Ánh xạ chuẩn Ánh xạ chính tắc
• Ánh xạ phân loại Ánh xạ phân loại
• Ánh xạ bảo giác: ánh xạ giữ nguyên độ lớn của các góc, nghĩa là góc giữa các tiếp tuyến của hai đường cong tại giao điểm của chúng bằng góc giữa các tiếp tuyến của các ảnh của hai đường tại giao điểm tương ứng. Một hàm song chỉnh hình là một ánh xạ bảo giác.
• Ánh xạ không thay đổi
• Ánh xạ nâng lên
• Ánh xạ liên tục:
  • Ánh xạ f từ x₀ $\in <!--\; \in \; -->$ X vào Y nếu với mỗi lân cận W của f(x₀) tồn tại một lân cận V của x₀ trong X (V $\subset <!--\; \subset \; -->$ X) sao cho f(V) $\subset <!--\; \subset \; -->$ W thì f được gọi là ánh xạ liên tục tại x₀ vào Y
  • Ánh xạ Y = f(X) được gọi là ánh xạ liên tục từ X vào Y nếu nó liên tục với mọi x $\in <!--\; \in \; -->$ X
• Ánh xạ đồng phôi: f:X→Y là ánh xạ song ánh, liên tục và ánh xạ ngược $f^{-<!--\; -\; -->1}$ cũng liên tục. Khi đó, X và Y được gọi là hai không gian đồng phôi hoặc tương đương tô pô.
• Phương ánh các đường nằm ngang Phương ánh các đường nằm ngang
• Ánh xạ co Ánh xạ co là ánh xạ của không gian mêtric vào chính nó, sao cho khoảng cách giữa hai điểm bất kỳ bị giảm đi qua ánh xạ đó. Nếu không gian mêtric đủ điều kiện, mỗi ánh xạ co luôn có một và chỉ một điểm bất động x, tức là F(x) = x.
• Ánh xạ đẳng biến Ánh xạ đẳng biến
• Ánh xạ định giá Ánh xạ định giá
• Ánh xạ cắt Ánh xạ cắt
• Ánh xạ phân thớ Ánh xạ phân thớ, ánh xạ các không gian phân thớ
• Ánh xạ đồng nhất hoá Ánh xạ đồng nhất hoá
• Ánh xạ nhúng chìm Ánh xạ nhúng chìm
• Ánh xạ trong Ánh xạ trong
• Ánh xạ đối hợp Ánh xạ đối hợp
• Ánh xạ chuẩn gián đoạn Ánh xạ chuẩn gián đoạn (khắp nơi có các điểm gián đoạn)
• Ánh xạ hạ thấp Ánh xạ hạ thấp
• Ánh xạ chính quy Ánh xạ chính quy
• Ánh xạ đơn hình Ánh xạ đơn hình
• Ánh xạ tenxơ Ánh xạ tenxơ
• Ánh xạ afin Ánh xạ afin
• Ánh xạ giải tích Ánh xạ giải tích
• Ánh xạ song liên tục Ánh xạ song liên tục
• Ánh xạ chuỗi Ánh xạ chuỗi, ánh xạ dây chuyền
• Ánh xạ đóng Ánh xạ đóng: f:X→Y được gọi là ánh xạ đóng nếu với mọi tập A đóng $\in <!--\; \in \; -->$ X, thì f(A) là tập đóng trong Y.
• Ánh xạ mở Ánh xạ mở: f:X→Y được gọi là ánh xạ mở nếu với mọi tập A mở $\in <!--\; \in \; -->$ X, thì f(A) là tập mở trong Y.
• Ánh xạ khả vi Ánh xạ khả vi
• Ánh xạ toàn hình Ánh xạ toàn hình
• Ánh xạ đồng cấu Ánh xạ đồng cấu
• Ánh xạ đồng luân Ánh xạ đồng luân
• Ánh xạ đẳng cự
• Ánh xạ bảo toàn thứ tự Ánh xạ bảo toàn thứ tự
• Ánh xạ tuyến tính
• Ánh xạ phân hình Ánh xạ phân hình
• Ánh xạ đơn cấu Ánh xạ đơn cấu
• Ánh xạ đơn điệu Ánh xạ đơn điệu
• Ánh xạ không thay phiên Ánh xạ không thay phiên
• Ánh xạ bảo toàn chuẩn Ánh xạ bảo toàn chuẩn
• Ánh xạ một-một Ánh xạ một-một, hai chiều, (song ánh)
• Ánh xạ lệch Ánh xạ lệch
• Ánh xạ tiền đóng Ánh xạ tiền đóng
• Ánh xạ giả bảo giác Ánh xạ giả bảo giác
• Ánh xạ tựa bảo giác Ánh xạ tựa bảo giác
• Ánh xạ tựa mở Ánh xạ tựa mở
• Ánh xạ hữu tỷ Ánh xạ hữu tỷ
• Ánh xạ bảo toàn chiều Ánh xạ bảo toàn chiều
• Ánh xạ lên miền có lát cắt trong Ánh xạ lên miền có lát cắt trong
• Ánh xạ hình sao Ánh xạ hình sao
• Ánh xạ đối ngẫu ximplectic Ánh xạ đối ngẫu ximplectic
• Ánh xạ tô pô Ánh xạ tô pô
• Ánh xạ đơn diệp Ánh xạ đơn diệp

• Tập hợp
• Lý thuyết tập hợp
• Nhóm (đại số)
• Hàm số
• Ánh xạ ảnh
• Tô pô

Ghi chú

Liên kết ngoài

• Ánh xạ (toán học) tại Encyclopædia Britannica (tiếng Anh)
• Hoàng Xuân Sính, Đại số đại cương (tái bản lần thứ tám), 1972, Nhà xuất bản Giáo dục