Sức hút của Trái Đất

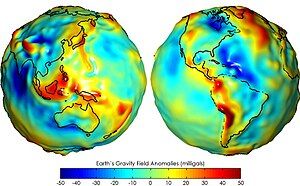
Trọng trường Trái Đất (Gravity of Earth), ký hiệu g, là lực hấp dẫn mà Trái Đất tác động lên các vật thể trên bề mặt hoặc gần bề mặt của nó. Trong hệ đơn vị SI, gia tốc này được đo bằng mét trên giây bình phương (m/s²), hoặc tương đương với Newton trên kilogram (N/kg). Giá trị trung bình của gia tốc này khoảng 9,81 m/s², nghĩa là, nếu không tính đến sự cản trở của không khí, một vật thể rơi tự do gần bề mặt Trái Đất sẽ tăng tốc thêm khoảng 9,81 m/s (32,2 ft/s) mỗi giây. Giá trị này đôi khi được gọi là g nhỏ, trong khi hằng số hấp dẫn G được gọi là G lớn.

Nghiên cứu về trọng trường Trái Đất thuộc lĩnh vực địa vật lý. Những phát hiện từ nghiên cứu này cũng có thể được áp dụng để mô tả trọng trường trên các hành tinh và thiên thể khác.

Trọng lực Trái Đất thực tế thay đổi tùy theo vị trí. Trên bề mặt Trái Đất, giá trị trung bình của trọng lực là 9,80665 m/s², với nhiều ký hiệu khác nhau như g_n, g_e (đôi khi được coi là giá trị pháp tuyến tại xích đạo là 9,78033 m/s²), g₀, hoặc đơn giản là g.

Trọng lượng của một vật trên bề mặt Trái Đất là lực kéo xuống của vật đó, theo Định Luật II Newton, được biểu thị bởi F = ma (lực kéo = trọng lượng x gia tốc). Gia tốc trọng trường ảnh hưởng đến gia tốc trọng lực, nhưng các yếu tố khác như sự tự quay của Trái Đất cũng tác động và thay đổi trọng lượng của vật. Trọng lực thường không tính đến lực hấp dẫn từ Mặt Trời hay Mặt Trăng (ảnh hưởng của thủy triều).

Biến động về cường độ

Một hình cầu hoàn hảo không xoay, có mật độ đồng nhất hoặc thay đổi chỉ theo khoảng cách từ tâm (đối xứng hình cầu), sẽ tạo ra một trường trọng lực đồng đều trên bề mặt của nó. Tuy nhiên, Trái Đất xoay quanh trục và không phải là hình cầu đối xứng do sự chênh lệch giữa hai cực, nên nó được coi là hình cầu dẹt. Do đó, trọng lực trên bề mặt Trái Đất khác nhau ở từng vị trí.

Trọng lực trên bề mặt Trái Đất thay đổi khoảng 0,7%, dao động từ 9,7639 m/s² tại đỉnh núi Nevado Huascarán ở Peru đến 9,8337 m/s² tại bề mặt biển Bắc Băng Dương. Tại các thành phố lớn, trọng lực dao động từ 9,7760 m/s² ở Kuala Lumpur, Thành phố Mexico và Singapore đến 9,825 m/s² ở Oslo và Helsinki.

Giá trị chuẩn

Vào năm 1901, tại Hội nghị toàn thể về Cân đo lần thứ ba, một giá trị chuẩn cho gia tốc trọng trường trên bề mặt Trái Đất đã được đề xuất là: g_n= 9,80665 m/s². Giá trị này dựa trên các đo lường thực hiện tại Pavillon de Breteuil gần Paris vào năm 1888, với điều chỉnh lý thuyết để chuyển đổi sang vĩ độ 45° ở mực nước biển. Đây không phải là giá trị tại một địa điểm cụ thể hay giá trị trung bình, mà chỉ là giá trị tạm thời để sử dụng, có thể được điều chỉnh khi có phát hiện mới.

Vĩ độ

Bề mặt Trái Đất liên tục chuyển động, nên nó không phải là hệ quy chiếu không quán tính. Ở các vĩ độ gần xích đạo, lực ly tâm do sự quay của Trái Đất tạo ra lớn hơn so với các vĩ độ gần hai cực. Điều này khiến trọng lực Trái Đất giảm nhẹ, tối đa là 0,3% tại xích đạo, làm giảm đáng kể gia tốc hướng xuống của các vật thể rơi.

Một nguyên nhân chính nữa cho sự khác biệt về trọng lực ở các vĩ độ là do sự phình ra của đường xích đạo của Trái Đất (một phần do lực ly tâm khi quay), làm cho các vật thể ở xích đạo cách xa trung tâm Trái Đất hơn so với các vật ở hai cực. Vì lực hấp dẫn giữa hai vật thể (Trái Đất và vật thể) tỉ lệ nghịch với bình phương khoảng cách giữa chúng, nên một vật ở xích đạo trải qua lực hấp dẫn yếu hơn so với khi ở hai cực Trái Đất.

Tóm lại, sự phình ra của đường xích đạo và tác động của lực ly tâm do sự quay của Trái Đất khiến trọng lực ở mực nước biển dao động từ khoảng 9,780 m/s² tại xích đạo lên đến 9,832 m/s² tại các cực. Vì vậy, một vật sẽ nặng hơn khoảng 0,5% tại hai cực so với tại xích đạo.

Độ cao

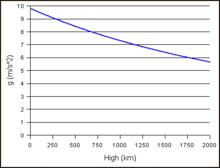
Trọng lực giảm khi độ cao tăng (và ngược lại), vì khoảng cách từ tâm Trái Đất tăng lên. Nếu mọi yếu tố khác không thay đổi, việc nâng cao độ cao từ mực nước biển lên 9000 m (30.000 ft) làm giảm trọng lượng khoảng 0,29% (Một yếu tố phụ ảnh hưởng đến trọng lượng là sự giảm mật độ không khí ở độ cao, làm giảm độ nổi của vật thể, điều này có thể làm tăng trọng lượng của một người ở độ cao 9000m khoảng 0,08%).

Có một hiểu lầm phổ biến rằng các phi hành gia trong quỹ đạo không có trọng lượng vì họ đã bay đủ cao để thoát khỏi lực hấp dẫn của Trái Đất. Thực tế, ở độ cao 400 km (250 dặm), lực hấp dẫn của Trái Đất vẫn tồn tại với gia tốc khoảng 8,68 m/s², tương đương với vận tốc vũ trụ cấp 1 là 7,66 km/s. Vì trạm quỹ đạo chuyển động với vận tốc này, hiện tượng rơi bên trong trạm không xảy ra (thả một chiếc thìa nó vẫn lơ lửng), tạo ra cảm giác 'không trọng lượng' (mặc dù lực hấp dẫn của Trái Đất vẫn còn).

Ảnh hưởng của độ cao lên trọng lực phụ thuộc vào mật độ của mặt đất (xem hình bên). Một trường hợp bay ở độ cao 30.000 ft so với mực nước biển trên núi sẽ cảm nhận trọng lực mạnh hơn so với khi ở cùng độ cao nhưng trên mặt biển. Tuy nhiên, một người đứng trên bề mặt Trái Đất sẽ cảm thấy trọng lực giảm dần khi độ cao tăng lên.

Công thức dưới đây cung cấp một xấp xỉ về trọng lực Trái Đất theo độ cao:

Trong đó:

• g_h là gia tốc trọng trường tại độ cao h so với mực nước biển
• R_e là bán kính Trái Đất
• g₀ là gia tốc trọng trường tiêu chuẩn

Trong công thức này, Trái Đất được coi là một khối cầu lý tưởng với phân bố khối lượng hoàn toàn đối xứng.

Độ sâu

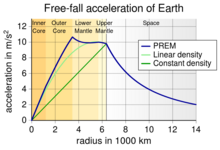
Một giá trị xấp xỉ cho trọng lực tại khoảng cách r từ tâm Trái Đất có thể được tính bằng cách giả định rằng mật độ của Trái Đất là một khối cầu đối xứng. Trọng lực chỉ phụ thuộc vào khối lượng bên trong khối cầu có bán kính r. Các tác động từ bên ngoài bị triệt tiêu do quy luật nghịch đảo bình phương của trọng lực. Kết quả là trọng lực có thể coi như tập trung toàn bộ khối lượng tại tâm. Do đó, gia tốc trọng trường tại bán kính này là:

Trong đó G là hằng số hấp dẫn, còn M(r) là tổng khối lượng trong bán kính r. Nếu giả sử mật độ của Trái Đất là không đổi với giá trị ρ, thì tổng khối lượng được tính là M(r) = (4/3)πρr. Do đó, sự thay đổi của trọng lực theo độ sâu được tính như sau:

Gia tốc trọng trường g tại độ sâu d có thể được tính bằng g'=g(1-d/R), với g là gia tốc trọng lực tại bề mặt Trái Đất. Ở đây, d là độ sâu và R là bán kính của Trái Đất. Nếu mật độ giảm dần từ ρ₀ tại trung tâm đến ρ₁ tại bề mặt, thì ρ(r) = ρ₀ − (ρ₀ − ρ₁) r / r_e và sự phụ thuộc được tính như sau:

Mối quan hệ giữa độ sâu, mật độ và trọng lực, được rút ra từ các nghiên cứu địa chấn qua thời gian (theo phương trình Adams-Williamson), được minh họa qua các biểu đồ dưới đây.

Địa hình và địa chất

Sự khác biệt về địa hình (như sự hiện diện của núi), địa chất (như mật độ đá xung quanh) và cấu trúc kiến tạo sâu hơn tạo ra sự biến đổi cục bộ và khu vực trong trường hấp dẫn của Trái Đất, gọi là dị thường hấp dẫn. Một số dị thường này rất lớn, dẫn đến hiện tượng phình ra ở mực nước biển và đồng hồ quả lắc không hoạt động đồng bộ.

Việc nghiên cứu những dị thường này là cơ sở của địa vật lý hấp dẫn. Các dao động được đo bằng thiết bị trọng lực có độ chính xác cao, sau khi loại bỏ ảnh hưởng của địa hình và các yếu tố khác đã biết, dữ liệu chính xác được thu thập. Những kỹ thuật này hiện được các nhà thăm dò địa chất sử dụng để tìm kiếm mỏ dầu và khoáng sản. Đá đặc hơn (thường chứa khoáng sản) tạo ra trường hấp dẫn cục bộ mạnh hơn trên bề mặt Trái Đất, trong khi đá trầm tích ít đặc hơn tạo ra trường hấp dẫn yếu hơn.

Các yếu tố khác

Trong không khí, các vật thể chịu tác động của lực nổi làm giảm cảm giác trọng lực (tức là trọng lượng của chúng). Mức độ của hiệu ứng này phụ thuộc vào mật độ không khí, và vì vậy liên quan đến áp suất không khí.

Sự ảnh hưởng của lực từ Mặt Trăng và Mặt Trời (nguyên nhân gây ra hiện tượng thủy triều) có tác động rất nhỏ đến cường độ trọng lực của Trái Đất, tùy thuộc vào vị trí tương đối của chúng; sự thay đổi điển hình là khoảng 2 µm/s (0,2 mGal) trong một ngày.

Sự thay đổi theo hướng

Gia tốc trọng trường là một đại lượng véc-tơ. Trong một Trái Đất đối xứng hình cầu, trọng lực sẽ chỉ hướng về tâm của quả cầu. Tuy nhiên, do Trái Đất hơi phẳng ở các cực, sẽ có những sai lệch nhỏ về hướng của trọng lực.

Các giá trị so sánh trên toàn thế giới

Có các công cụ để tính toán lực hấp dẫn tại các thành phố khác nhau trên toàn cầu. Ảnh hưởng của vĩ độ rất rõ ràng với lực hấp dẫn ở các thành phố vĩ độ cao như Anchorage (9,826 m/s), Helsinki (9,825 m/s), lớn hơn khoảng 0,5% so với các thành phố gần xích đạo như Kuala Lumpur (9,776 m/s) và Manila (9,780 m/s). Ảnh hưởng của độ cao có thể thấy ở thành phố Mexicô (9,776 m/s; độ cao 2,240 m (7.350 ft)) và khi so sánh với Denver (9,798 m/s; 1.616 m (5.302 ft)) và Washington, DC (9.801 m/s; 30 m (98 ft)), cả ba đều gần 39° Bắc. Các giá trị đo được có thể tham khảo trong cuốn sách T.M. Yarwood và F. Castle, Macmillan, phiên bản sửa đổi 1970.

Mô hình toán học

Mô hình vĩ độ

Nếu địa hình đang ở mực nước biển, ta có thể ước tính gia tốc trọng trường tại vĩ độ bằng công thức: $g\left\{\mathrm{\varphi <!--\; \varphi \; -->}\right\}$, tại vĩ độ $\mathrm{\varphi <!--\; \varphi \; -->}$:

Đây là công thức trọng lực quốc tế năm 1967, hay còn gọi là công thức hệ thống tham chiếu trắc địa 1967, phương trình Helmert hoặc công thức Clairaut.

Một công thức thay thế cho g dưới dạng hàm của vĩ độ là công thức trọng lực Ellipsoidal trong hệ thống trắc địa thế giới WGS 84.

$g\left\{\mathrm{\varphi \; <div\; class="min-w-[250px]\; max-w-[94vw]\; md:max-w-[770px]">\; <ins\; class="adsbygoogle"\; style="display:block;\; text-align:center;"\; data-ad-layout="in-article"\; data-ad-format="fluid"\; data-ad-client="ca-pub-9247024304160346"\; data-ad-slot="4115752014"></ins>\; </div>\; <!--\; \varphi \; -->}\right\}=G_e\left[\frac{1+k{\sin }^2<!--\; \; -->\mathrm{\varphi <!--\; \varphi \; -->}}{\sqrt{1-<!--\; -\; -->e^2{\sin }^2<!--\; \; -->\mathrm{\varphi <!--\; \varphi \; -->}}}\right],$

Các thành phần bao gồm:

• $a,b$ lần lượt là các bán trục xích đạo và cực của hình ellipsoid
• $e^2=1-<!--\; -\; -->(b/a{)}^2$ là bình phương của độ lệch tâm của hình ellipsoid
• $G_e,G_p$ là trọng lực tại xích đạo và cực tương ứng
• $k=\frac{b{G}_p-<!--\; -\; -->a{G}_e}{a{G}_e}$ là hằng số trong công thức

Trong đó $G_p=9.8321849378m\cdot <!--\; \cdot \; -->s^{-<!--\; -\; -->2}$,

$g\left\{\mathrm{\varphi <!--\; \varphi \; -->}\right\}=9.7803253359m\cdot <!--\; \cdot \; -->s^{-<!--\; -\; -->2}\left[\frac{1+0.00193185265241{\sin }^2<!--\; \; -->\mathrm{\varphi <!--\; \varphi \; -->}}{\sqrt{1-<!--\; -\; -->0.00669437999013{\sin }^2<!--\; \; -->\mathrm{\varphi <!--\; \varphi \; -->}}}\right]$.

Sự khác biệt giữa công thức WGS-84 và phương trình Helmert nhỏ hơn 0.68 μm/s

Độ chính xác của không khí tự do

Điều chỉnh đầu tiên cho mô hình dựa trên độ chính xác của không khí tự do (FAC), liên quan đến độ cao so với mực nước biển. Gần bề mặt Trái Đất (mực nước biển), trọng lực giảm theo độ cao, và việc ngoại suy tuyến tính cho thấy trọng lực sẽ bằng không ở độ cao bằng một nửa bán kính Trái Đất (9,8 m/s trên mỗi 3.200 km). Tốc độ giảm được tính bằng cách phân biệt g(r) đối với r và khai triển với r=r_{Trái Đất}.

Sử dụng khối lượng và bán kính của Trái Đất, ta có:

$r_{\mathrm{Trái}\mathrm{Đất}}=6.371\cdot <!--\; \cdot \; -->{10}^{6}m$

$m_{\mathrm{Trái}\mathrm{Đất}}=5.9722\cdot <!--\; \cdot \; -->{10}^{24}\mathrm{kg}$

Hệ số điều chỉnh FAC (Δg) có thể được tính dựa trên gia tốc trọng lực theo hằng số hấp dẫn G, như được xác định bởi định luật vạn vật hấp dẫn (xem thêm dưới đây):

$g_0=G{M}_{\mathrm{Trái}\mathrm{Đất}}/R_{\mathrm{Trái}\mathrm{Đất}}^2=9.8196\frac{m}{s^2}$

Cụ thể là:

$G=6.67384\cdot <!--\; \cdot \; -->{10}^{-<!--\; -\; -->11}\frac{m^3}{\mathrm{kg}g\cdot <!--\; \cdot \; -->s^2}.$

Tại độ cao h tính từ mặt đất, giá trị của gh được xác định bởi công thức sau:

$g_h=G{M}_e/{\left(R_e+h\right)}^2$

Do đó, FAC cho mỗi độ cao h tính từ bán kính Trái Đất có thể được thể hiện như sau:

$\mathrm{\Delta <!--\; \Delta \; -->}{g}_h=\left[G{M}_e/{\left(R_e+h\right)}^2\right]-<!--\; -\; -->\left[G{M}_e/R_e^2\right]$

Biểu thức trên có thể được áp dụng trực tiếp trong lập trình hoặc bảng tính. Bạn có thể thu gọn các thuật ngữ, đơn giản hóa và bỏ qua những yếu tố nhỏ (h<<r_{Trái Đất}), mặc dù điều này chỉ cho phép ước lượng gần đúng.

$\mathrm{\Delta <!--\; \Delta \; -->}{g}_h\approx <!--\; \approx \; -->-<!--\; -\; -->\frac{G{M}_e}{R_e^2}\cdot <!--\; \cdot \; -->\frac{2h}{R_e}$

Áp dụng các giá trị số nêu trên cho một chiều cao h nhất định tính bằng mét, ta có:

$\mathrm{\Delta <!--\; \Delta \; -->}{g}_h\approx <!--\; \approx \; -->-<!--\; -\; -->3.086\cdot <!--\; \cdot \; -->{10}^{-<!--\; -\; -->6}h$

Khi kết hợp yếu tố vĩ độ và FAC, công thức phổ biến nhất thường được trình bày như sau:

$g\{\mathrm{\varphi <!--\; \varphi \; -->},h\}=g\left\{\mathrm{\varphi <!--\; \varphi \; -->}\right\}-<!--\; -\; -->3.086\cdot <!--\; \cdot \; -->{10}^{-<!--\; -\; -->6}h$

Trong đó: $g\{\mathrm{\varphi <!--\; \varphi \; -->},h\}$ đại diện cho gia tốc trọng lực với đơn vị m/s² tại vĩ độ $\mathrm{\varphi <!--\; \varphi \; -->}$ và độ cao h (mét)

Các khối kiến tạo

Đối với địa hình phẳng tại mực nước biển, cần thêm một thuật ngữ phụ để điều chỉnh trọng lực do sự gia tăng khối lượng; trong trường hợp này, khối lượng bổ sung có thể được coi như một lớp vô hạn và ta tính được gấp 2πG lần khối lượng trên một đơn vị diện tích, tương đương với 4,2×10 m³•s•kg (0,042 μGal•kg•m²) (hiệu chỉnh Bouguer). Đối với mật độ đá trung bình là 2,67 g•cm thì ta có 1,1×10 s (0.11 mGal•m). Kết hợp với độ chính xác không khí tự do, điều này có nghĩa là trọng lực tại bề mặt Trái Đất giảm 2 µm•s (0,20 mGal) cho mỗi mét độ cao của địa hình. (Hai hiệu ứng này sẽ bị hủy nếu mật độ đá bề mặt là 4/3 lần mật độ trung bình của toàn Trái Đất. Với mật độ toàn Trái Đất là 5,515 g•cm, đứng trên một khối đá như sắt có mật độ trên 7,35 g•cm sẽ làm tăng trọng lượng.)

Khi tính toán trọng lực dưới bề mặt Trái Đất, chúng ta cần áp dụng cả hiệu chỉnh không khí tự do và hiệu chỉnh Bouguer kép. Mô hình mảng vô hạn cho thấy việc di chuyển điểm quan sát dưới mảng sẽ thay đổi trọng lực do mảng đó và điểm đối diện với nó. Thay vào đó, chúng ta có thể coi Trái Đất như một hình cầu đối xứng và trừ khối lượng của lớp vỏ Trái Đất khỏi khối lượng toàn Trái Đất tại điểm quan sát, vì điều này không làm thay đổi trọng lực bên trong. Kết quả sẽ tương tự như vậy.

Ước lượng g theo định luật vạn vật hấp dẫn

Theo định luật vạn vật hấp dẫn, lực tác dụng lên một vật thể từ trọng lực của Trái Đất được tính như sau:

$F=G\frac{m_1{m}_2}{r^2}=\left(G\frac{m_1}{r^2}\right)m_2$

Trong đó: r là khoảng cách từ tâm Trái Đất đến bề mặt (xem chi tiết bên dưới), với m₁ là khối lượng của Trái Đất và m₂ là khối lượng của vật thể tại bề mặt.

Hơn nữa, theo định luật thứ hai của Newton, F = ma, với m là khối lượng và a là gia tốc, ta có thể xác định:

$F=m_{2}g$

Khi so sánh hai công thức này, chúng ta nhận được:

$g=G\frac{m_1}{r^2}$

Do đó, để tính gia tốc trọng lực tại mực nước biển, hãy thay thế các giá trị của hằng số hấp dẫn, G, khối lượng của Trái Đất (đo bằng kg), m₁, và bán kính Trái Đất (đo bằng mét), r, để tính giá trị của g.

$g=G\frac{m_1}{r^2}=6.67384\cdot <!--\; \cdot \; -->{10}^{-<!--\; -\; -->11}{m}^3\cdot <!--\; \cdot \; -->{kg}^{-<!--\; -\; -->1}\cdot <!--\; \cdot \; -->s^{-<!--\; -\; -->2}\frac{5.9722\cdot <!--\; \cdot \; -->{10}^{24}kg}{(6.371\cdot <!--\; \cdot \; -->{10}^{6}m{)}^2}=9.8196\text{m}\cdot <!--\; \cdot \; -->{\text{s}}^{-<!--\; -\; -->2}$

Lưu ý rằng công thức này chỉ chính xác khi xem xét Trái Đất như một vật thể đồng nhất, tức là khi khối lượng của nó được coi như tập trung tại tâm của Trái Đất. Điều này cho phép chúng ta sử dụng r làm bán kính của Trái Đất.

Giá trị tính được gần như trùng khớp với giá trị thực tế của g. Sự khác biệt có thể do một số yếu tố như sau:

• Trái Đất không đồng nhất về mặt vật lý
• Trái Đất không phải là hình cầu hoàn hảo, nên cần phải sử dụng giá trị trung bình của bán kính
• Giá trị tính toán của g chỉ phản ánh trọng lực thực sự. Nó không tính đến lực giảm do sự quay của Trái Đất và các lực hấp dẫn bị phản lại bởi lực ly tâm.

Có một số sai số đáng kể trong các giá trị của r và m₁ dùng trong tính toán, và giá trị của G cũng khó đo chính xác.

Nếu chúng ta có các giá trị của G, g, và r, ta có thể tính ngược để ước lượng khối lượng của Trái Đất. Phương pháp này đã được Henry Cavendish áp dụng.

Đối tượng nghiên cứu

• Trái Đất
• Hành tinh
• v.v

• Định luật vạn vật hấp dẫn của Newton
• Tương tác hấp dẫn
• Dị thường trọng lực
• Khảo sát trọng lực
• Khám phá Trường Trọng lực và Tuần hoàn Đại dương Ổn định
• Thí nghiệm Khôi phục Trọng lực và Khí hậu (GRACE)

Liên kết ngoài