T-Phân phối là gì?
T-Phân phối, hay còn gọi là T-Phân phối của Sinh viên, là một loại phân phối xác suất tương tự như phân phối chuẩn với hình dạng chuông nhưng có đuôi dày hơn. Nó được sử dụng để ước tính các tham số của quần thể cho các mẫu nhỏ hoặc phương sai không xác định. T-Phân phối có khả năng cao hơn để xuất hiện giá trị cực đoan so với phân phối chuẩn, và do đó có đuôi dày hơn.
T-Phân phối là cơ sở để tính toán các kiểm định t trong thống kê.
Điểm Chính
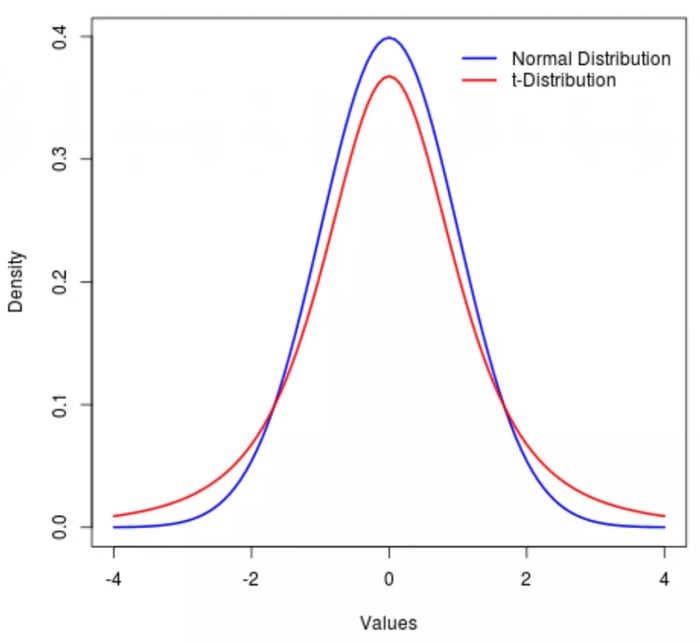
T-Phân phối, giống như phân phối chuẩn, có hình dạng chuông và đối xứng, nhưng có đuôi dày hơn, điều này có nghĩa là nó có xu hướng sản sinh ra các giá trị rơi xa khỏi giá trị trung bình của nó.
Kiểm định t được sử dụng trong thống kê để ước tính tính chất quan trọng.
Khi một mẫu gồm n quan sát được lấy ra từ một quần thể có phân phối chuẩn có trung bình M và độ lệch chuẩn D, giá trị trung bình mẫu m và độ lệch chuẩn mẫu d sẽ khác so với M và D do sự ngẫu nhiên của mẫu.
Điểm z có thể được tính toán với độ lệch chuẩn của quần thể như Z = (x - M)/D, và giá trị này có phân phối chuẩn với trung bình 0 và độ lệch chuẩn 1. Nhưng khi sử dụng độ lệch chuẩn ước tính, một điểm t được tính toán như T = (m - M)/{d/sqrt(n)}, và sự khác biệt giữa d và D khiến phân phối trở thành một t-phân phối với (n - 1) độ tự do thay vì phân phối chuẩn với trung bình 0 và độ lệch chuẩn 1.
Ví dụ về Cách Sử Dụng T-Phân Phối
Hãy xem ví dụ sau về cách sử dụng t-phân phối trong phân tích thống kê. Đầu tiên, hãy nhớ rằng một khoảng tin cậy cho trung bình là một phạm vi giá trị, được tính từ dữ liệu, nhằm bắt giữ một giá trị trung bình của “quần thể”. Khoảng này là m +- t*d/sqrt(n), trong đó t là giá trị quan trọng từ t-phân phối.
Ví dụ, một khoảng tin cậy 95% cho tỷ lệ lợi nhuận trung bình của Chỉ số Công nghiệp Dow Jones (DJIA) trong 27 ngày giao dịch trước ngày 11 tháng 9 năm 2001, là -0.33%, (+/- 2.055) * 1.07 / sqrt(27), cho một tỷ lệ lợi nhuận trung bình ổn định khoảng giữa -0.75% và +0.09%. Số 2.055, số lượng lỗi chuẩn cần điều chỉnh, được tìm thấy từ t-phân phối.
Bởi vì phân phối t- có đuôi dày hơn phân phối chuẩn, nó có thể được sử dụng như một mô hình cho các lợi nhuận tài chính có độ nhọn vượt trội, từ đó cho phép tính toán giá trị rủi ro (VaR) một cách hiệu quả hơn trong các trường hợp như vậy.
Phân phối t so với phân phối chuẩn
Phân phối chuẩn được sử dụng khi phân phối dân số được giả định là chuẩn. Phân phối t tương tự như phân phối chuẩn, chỉ có đuôi dày hơn. Cả hai giả định một dân số có phân phối chuẩn. Do đó, phân phối t có độ nhọn cao hơn so với phân phối chuẩn. Xác suất của việc có giá trị rất xa so với giá trị trung bình lớn hơn với phân phối t hơn là với phân phối chuẩn.
Giới hạn của việc sử dụng phân phối t
Phân phối t có thể làm biến đổi sự chính xác so với phân phối chuẩn. Điều này chỉ xảy ra khi cần sự chuẩn xác hoàn hảo. Phân phối t nên chỉ được sử dụng khi độ lệch chuẩn của dân số không được biết. Nếu độ lệch chuẩn của dân số được biết và kích thước mẫu đủ lớn, phân phối chuẩn nên được sử dụng để có kết quả tốt hơn.
Phân phối t trong thống kê là gì?
Phân phối t được sử dụng trong thống kê để ước tính các tham số của dân số cho kích thước mẫu nhỏ hoặc phương sai chưa xác định. Nó còn được gọi là phân phối t của Student.
Khi nào nên sử dụng phân phối t?
Phân phối t nên được sử dụng nếu kích thước mẫu của dân số nhỏ và độ lệch chuẩn không được biết. Nếu không, thì nên sử dụng phân phối chuẩn.
Ý nghĩa của phân phối chuẩn là gì?
Phân phối chuẩn là thuật ngữ chỉ đường cong chuông xác suất. Nó còn được gọi là phân phối Gaussian.
Điểm quan trọng
Phân phối t được sử dụng trong thống kê để ước tính tính chất quan trọng của dân số cho kích thước mẫu nhỏ hoặc các biến thể chưa biết. Giống như phân phối chuẩn, nó có hình chuông và đối xứng. Khác với phân phối chuẩn, nó có đuôi dày hơn, dẫn đến khả năng xuất hiện các giá trị cực đoan cao hơn.
