Tài liệu bài tập tổng hợp môn Toán lớp 7, Chương 8 từ sách Chân trời sáng tạo với đáp án đi kèm
Câu 1. Xem hình vẽ dưới đây. Khi đó:
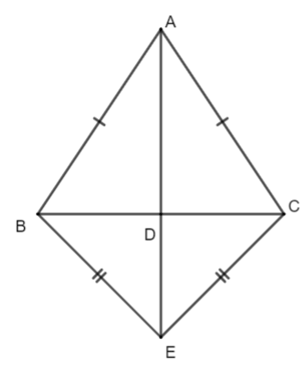
A. AE là đường trung trực của đoạn thẳng BC;
B. D là điểm giữa của AE;
C. D cách đều hai điểm A và E;
D. Tất cả các đáp án trên đều không đúng
Đáp án chính xác là: A. AE là đường trung trực của đoạn thẳng BC;
Chúng ta có: A cách đều hai điểm B và C (AB = AC).
E cũng cách đều hai điểm B và C (EB = EC).
Vì vậy, AE là đường trung trực của đoạn BC (theo định nghĩa đường trung trực).
Câu 2. Xét tam giác ABC, với E và D lần lượt là trung điểm của AB và BC. Khi kẻ đường trung trực từ E và D, chúng cắt nhau tại O. F là trung điểm của AC. Khi đó:
A. OF là đường trung tuyến;
B. OF là đường trung trực của đoạn AC;
C. O là trực tâm của tam giác ABC;
D. Cả B và C đều đúng.
Đáp án chính xác là: D. Cả B và C đều đúng.
Xem xét tam giác ABC với:
OE là đường trung trực của đoạn AB (theo giả thiết);
OD là đường trung trực của đoạn BC (theo giả thiết);
OE và OD giao nhau tại điểm O.
Vì vậy, O chính là trực tâm của tam giác ABC.
Hơn nữa, F là trung điểm của đoạn AC.
Do đó, OF là đường trung trực của đoạn AC.
Vì vậy, các đáp án B và C đều chính xác.
Câu 3. Trong một khu dân cư có ba điểm D, E, F, người ta dự định xây dựng một công viên H sao cho H cách đều cả ba điểm dân cư (như hình vẽ).
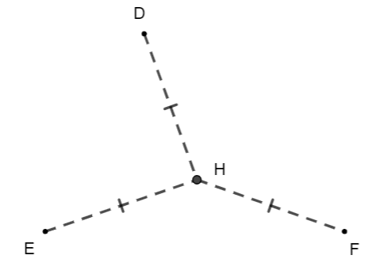
Khi đó, vị trí của H sẽ là:
A. Điểm giữa của đoạn EF;
B. Trung điểm của tam giác DEF;
C. Điểm giao nhau của ba đường trung trực trong tam giác DEF;
D. A và C đều chính xác.
Đáp án chính xác là: C. Điểm giao nhau của ba đường trung trực trong tam giác DEF;
Xem xét ba điểm dân cư D, E, F tạo thành các đỉnh của tam giác DEF
Để xây dựng công viên H sao cho H cách đều ba điểm dân cư, thì H cần phải cách đều ba đỉnh của tam giác DEF.
Do đó, H là điểm giao nhau của ba đường trung trực trong tam giác DEF.
Câu 4. Trong tam giác ABC, với E và F lần lượt là trung điểm của AB và BC. Giả sử O là điểm cách đều ba đỉnh của tam giác ABC. Khi đó:
A. OE vuông góc với đoạn AC;
B. OE vuông góc với đoạn AB;
C. OF vuông góc với đoạn AC;
D. OF vuông góc với đoạn AB.
Đáp án chính xác là: B. OE vuông góc với đoạn AB;
Xem xét tam giác ABC với điểm O cách đều ba đỉnh của tam giác ABC.
Do đó, O là điểm giao nhau của ba đường trung trực trong tam giác ABC.
Hơn nữa, E là trung điểm của đoạn AB.
Vì vậy, OE là đường trung trực của đoạn AB.
Do đó, OE vuông góc với đoạn AB tại điểm E.
Câu 5. Trong tam giác cân ABC tại A, hai đường trung tuyến BH và CK cắt nhau tại điểm G. Biết rằng BG = 6 cm. Độ dài của đoạn CK là:
A. 9 cm;
B. 10 cm;
C. 12 cm;
D. 8 cm.
Đáp án đúng là: A
Câu 6. Trong tam giác ABC, hai đường trung tuyến AD và CE giao nhau tại G. Đường thẳng BG cắt đoạn AC tại điểm F. Biết rằng AC = 10 cm. Tính độ dài của đoạn AF:
A. 10 cm;
B. 4 cm;
C. 5 cm;
D. 8 cm.
Đáp án chính xác là: C
Xem xét tam giác ABC với:
AD là một đường trung tuyến (theo giả thiết);
BE là một đường trung tuyến (theo giả thiết).
AD và BE giao nhau tại điểm G.
Do đó, G là điểm giao nhau của ba đường trung tuyến trong tam giác ABC.
Kết luận rằng BG là một đường trung tuyến của tam giác ABC.
Vì vậy, F là trung điểm của đoạn AC.
Chúng ta có: AF = AC / 2 = 5 (cm)
Do đó, độ dài của đoạn AF là 5 cm.
Câu 7. Trong tam giác ABC, với đường cao BE và trực tâm K. Gọi H là điểm giao nhau của AK và BC. Từ điểm C, kẻ đường thẳng vuông góc với BC cắt AB tại điểm D. Khẳng định nào dưới đây là chính xác?
A. CD song song với AH;
B. CD song song với AB;
C. CD song song với BE;
D. CD vuông góc với BE;
Đáp án chính xác là: A
Xem xét tam giác ABC với:
K là trực tâm của tam giác (theo giả thiết);
AK cắt đoạn BC tại điểm H (theo giả thiết).
Vì vậy, AH là đường cao của tam giác ABC.
Do đó, AH vuông góc với BC tại điểm H.
Hơn nữa, CD cũng vuông góc với BC tại điểm C.
Vì vậy, CD song song với AH.
Câu 8. Trong tam giác ABC cân tại A, với G là trọng tâm và I là điểm nằm trong tam giác, cách đều ba cạnh của tam giác đó. Khẳng định nào dưới đây là chính xác?
A. Ba điểm A, G và I nằm trên cùng một đường thẳng;
B. Điểm G nằm trên đường phân giác của góc B;
C. Điểm G cách đều ba đỉnh của tam giác ABC;
D. Điểm G cách đều ba cạnh của tam giác ABC.
Đáp án chính xác là: A. Ba điểm A, G và I nằm trên cùng một đường thẳng;
Gọi M là điểm giao nhau của AI và BC.
Vì I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác ABC, nên I nằm trên các đường phân giác của tam giác ABC.
Do đó, I nằm trên đường phân giác AM của góc BAC.
Hơn nữa, vì tam giác ABC cân tại A, đường phân giác AM cũng là đường trung tuyến của tam giác ABC.
Vậy I nằm trên đường thẳng AM.
Ngoài ra, G cũng nằm trên đường thẳng AM (vì G là trọng tâm của tam giác ABC).
Vì vậy, ba điểm A, G và I nằm trên cùng một đường thẳng.
Câu 9. Một hòn đảo có đường bờ biển tạo thành hình tam giác. Các đường bờ biển được ký hiệu là m, n, p (như hình vẽ). Để đặt một ngọn hải đăng trên hòn đảo sao cho khoảng cách từ ngọn hải đăng đến ba đường bờ biển bằng nhau, vị trí của ngọn hải đăng nên là:
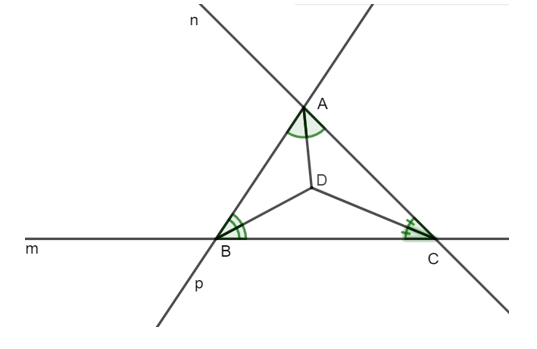
A. Điểm giao nhau của ba đường trung tuyến của tam giác;
B. Điểm giao nhau của ba đường trung trực của tam giác;
C. Điểm giao nhau của ba đường cao trong tam giác;
D. Điểm giao nhau của ba đường phân giác trong tam giác.
Đáp án chính xác là: D. Điểm giao nhau của ba đường phân giác trong tam giác.
Gọi A, B, C là các điểm giao nhau của các đường bờ biển.
Gọi D là vị trí cần đặt ngọn hải đăng.
Để ngọn hải đăng cách đều ba đường bờ biển, điểm D cần phải cách đều ba cạnh AB, BC và AC.
Do đó, D là điểm giao nhau của ba đường phân giác trong tam giác ΔABC.
Vị trí chính xác của ngọn hải đăng sao cho khoảng cách từ nó đến ba đường bờ biển đều bằng nhau là điểm giao nhau của ba đường phân giác trong tam giác.
Câu 10. Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào có thể là ba cạnh của một tam giác?
A. 2 cm; 3 cm; 6 cm;
B. 3 cm; 6 cm; 3 cm;
C. 3 cm; 4 cm; 5 cm;
D. 5 cm; 6 cm; 7 dm.
Đáp án đúng là: C. 3 cm; 4 cm; 5 cm;
+ Xem xét bộ ba: 2 cm; 3 cm; 6 cm
Có 2 cm + 3 cm = 5 cm < 6 cm
Vậy bộ ba đoạn thẳng 2 cm, 3 cm, 6 cm không thể tạo thành một tam giác.
+ Xem bộ ba: 3 cm; 6 cm; 3 cm
Có 3 cm + 3 cm = 6 cm
Do đó bộ ba đoạn thẳng 3 cm, 6 cm, 3 cm cũng không tạo thành một tam giác.
+ Xem xét bộ ba đoạn thẳng: 3 cm, 4 cm, 5 cm
Có: 4 cm – 3 cm < 5 cm < 4 cm + 3 cm.
Vậy bộ ba đoạn thẳng 3 cm, 4 cm, 5 cm có thể tạo thành một tam giác.
+ Xem xét bộ ba đoạn thẳng: 5 cm, 6 cm, 7 dm
Chuyển đổi 7 dm = 70 cm.
Vì 5 cm + 6 cm < 70 cm.
Do đó, bộ ba đoạn thẳng 5 cm, 6 cm, 7 dm không thể tạo thành một tam giác.
Câu 11: Xét tam giác ABC với AB = 2 cm, BC = 8 cm. Độ dài của cạnh AC là một số nguyên tố. Tính chu vi của tam giác ABC:
A. 18 cm;
B. 7 cm;
C. 17 cm;
D. 19 cm.
Đáp án chính xác là: C. 17 cm;
Giả sử độ dài của cạnh AC là x (x > 0) (cm)
Áp dụng bất đẳng thức tam giác, ta có: BC – AB < AC < BC + AB
Do đó 8 – 2 < x < 8 + 2
Ta có 6 < x < 10

Vì x là số nguyên tố
Kết luận x = 7
Vậy AC = 7 (cm)
Chu vi của tam giác ABC được tính bằng:
AB + AC + BC = 2 + 7 + 8 = 17 (cm).
Do đó, chu vi tam giác ABC là 17 cm.
Câu 12: Trong tam giác ABC với AH vuông góc BC (H thuộc BC). Chọn câu sai.
A. Nếu AB < AC thì BH < HC;
B. Nếu AB > AC thì BH < HC;
C. Nếu AB = AC thì BH = HC;
D. Nếu BH > HC thì AB > AC.
Đáp án chính xác là: B. Nếu AB > AC thì BH < HC;
Trong tam giác ABC với AH là đường vuông góc và BH, CH là hai hình chiếu.
Vậy:
+ Nếu AB < AC thì BH < HC (câu A đúng);
+ Nếu AB > AC thì BH > HC (câu B sai);
+ Nếu AB = AC thì BH = HC (câu C đúng);
+ Nếu BH > HC thì AB > AC (câu D đúng).
