Tam giác cân là gì? Khám phá định nghĩa, đặc điểm, cách chứng minh và bài tập

Ngoài tam giác vuông và tam giác đều, tam giác cân cũng là một loại tam giác đặc biệt. Mỗi loại tam giác có những khái niệm và tính chất riêng. Để hiểu thêm về tam giác cân, hãy cùng theo dõi bài viết dưới đây để nắm rõ định nghĩa, tính chất và cách chứng minh tam giác cân.

1. Khái niệm về tam giác cân

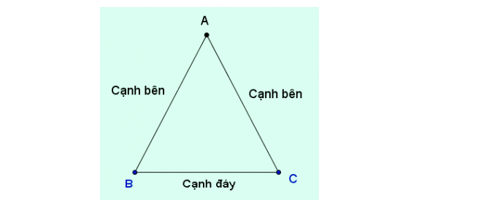
Tam giác cân là loại tam giác có hai cạnh bằng nhau, gọi là các cạnh bên. Đỉnh của tam giác cân là giao điểm của hai cạnh bên, còn góc tại đỉnh gọi là góc đỉnh, hai góc còn lại gọi là góc đáy.

Trong một tam giác cân, trực tâm, trọng tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp đều nằm trên cùng một đường thẳng. Đường thẳng này đồng thời là đường trung tuyến, đường phân giác, đường trung trực và đường cao ứng với cạnh đáy. Để hiểu rõ hơn về định nghĩa và tính chất của tam giác cân, mời bạn xem hình ảnh minh họa dưới đây.

Tam giác cân

Xem xét tam giác ABC với AB = AC, ta có tam giác ABC là tam giác cân. Trong đó, BC là cạnh đáy, AB và AC là hai cạnh bên, và tam giác ABC cân tại đỉnh A. Góc B và góc C là các góc đáy, còn A là góc tại đỉnh.

Tam giác cân có thể được phân loại thành ba dạng khác nhau:

- Tam giác nhọn cân: Đây là loại tam giác có ba góc đều nhỏ hơn 90° và ít nhất hai góc trong số đó có số đo bằng nhau. Ví dụ, các góc của một tam giác nhọn cân có thể là 50°, 50° và 80°.

- Tam giác vuông cân: Đây là một ví dụ về tam giác vuông có hai cạnh bằng nhau (cùng các góc tương ứng).

- Tam giác tù cân: Loại tam giác này có một góc tù (từ 90° đến 180°) và hai góc nhọn còn lại có số đo giống nhau. Ví dụ về góc của tam giác tù cân có thể là 30°, 30° và 120°.

2. Các đặc điểm của tam giác cân

Mỗi loại hình trong hình học đều có những đặc điểm riêng biệt giúp phân biệt chúng với các hình khác. Đối với tam giác cân, các đặc điểm nổi bật của nó bao gồm:

Tính chất 1: Trong một tam giác cân, hai góc ở đáy luôn bằng nhau. Ví dụ, nếu ΔABC là tam giác cân tại đỉnh A, thì hai góc ở đáy là góc ABC và góc ACB sẽ bằng nhau.

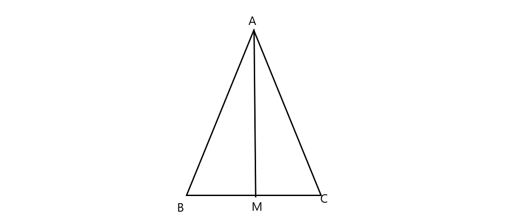
Trong tam giác cân ABC, giả sử AM là tia phân giác của góc BAC.

Vậy ta có: Góc BAM bằng Góc CAM.

Xem xét tam giác ABM và tam giác ACM, với điều kiện AB = AC (đã cho).

Góc BAM bằng Góc CAM (theo chứng minh)

AM là chung

Do đó, ΔABM đồng dạng với ΔACM (theo cạnh-góc-cạnh) dẫn đến Góc ABC bằng Góc ACB (đã chứng minh).

Tính chất 2: Một tam giác sẽ là tam giác cân nếu nó có hai góc bằng nhau.

Ví dụ: Xem xét tam giác ΔABC, nếu góc ABC bằng góc ACB, thì ΔABC là tam giác cân tại A.

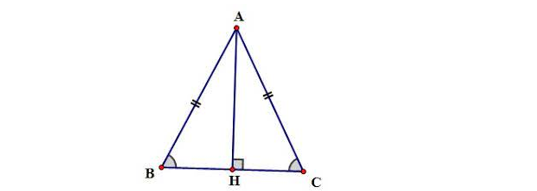
Trong tam giác ABC, AH là tia phân giác của góc BAC

=> Góc BAH bằng Góc CAH

Tam giác ΔABH có tổng ba góc BAH, AHB và ABH bằng 180 độ (tổng của các góc trong tam giác)

Tam giác ΔACH có tổng ba góc CAH, ACH và AHC bằng 180 độ (tổng của các góc trong tam giác)

Vì góc ABC bằng góc ACB nên góc AHB sẽ bằng góc AHC

Xem xét tam giác ABH và tam giác ACH với các điều kiện sau:

Góc BAH bằng Góc CAH

Góc ABC bằng Góc ACB

Góc AHB bằng Góc AHC

Từ đó, ΔABH bằng ΔACH (theo g.g.g) nên AB bằng AC (cạnh tương ứng giống nhau)

Xem xét tam giác ABC với AB = AC, do đó tam giác ABC là tam giác cân tại A (theo định nghĩa)

Tính chất 3: Trong tam giác cân, đường trung trực của cạnh đáy cũng chính là đường phân giác, đường trung tuyến, và đường cao của tam giác.

Tính chất 4: Nếu trong một tam giác, một đường trung tuyến đồng thời là đường trung trực, thì tam giác đó là tam giác cân.

3. Dấu hiệu nhận biết tam giác cân

Dựa vào các đặc điểm đã nêu, để nhận diện một tam giác cân, chúng ta có thể dựa vào độ dài các cạnh hoặc số đo các góc. Tam giác cân có hai dấu hiệu nhận diện như sau:

- Dấu hiệu 1: Nếu trong một tam giác, hai cạnh bên bằng nhau thì tam giác đó là tam giác cân.

- Dấu hiệu 2: Nếu trong một tam giác, hai góc bằng nhau thì tam giác đó là tam giác cân.

Ví dụ: Xem xét tam giác MNP với ΔMNE bằng ΔMPE. Chứng minh rằng tam giác MNP là tam giác cân.

Chứng minh theo dấu hiệu 1:

Dựa theo đề bài, chúng ta có: ΔMNE bằng ΔMPE, vì vậy ⇒ MN = MP

=> Tam giác MNP cân tại điểm M

- Chứng minh theo dấu hiệu 2:

Dựa theo đề bài, chúng ta có: ΔMNE bằng ΔMPE

Do đó ⇒ Góc N bằng Góc P

=> Tam giác MNP cân tại đỉnh M

4. Bài tập ứng dụng và phương pháp chứng minh tam giác cân

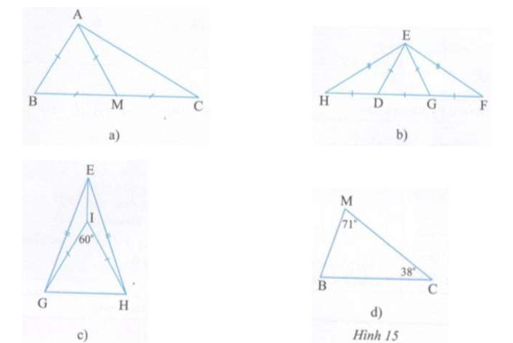
Bài 1: Trong các tam giác ở hình 15a, b, c, d, hãy xác định tam giác nào là tam giác cân, tam giác nào là tam giác đều và lý do tại sao?

Giải:

a) Với AB = BM = AM (theo giả thiết) => tam giác ABM là tam giác đều.

AM = CM (theo giả thiết) => tam giác MAC là tam giác cân tại M.

b) Với ED = DG = EG (theo giả thiết) => tam giác EDG là tam giác đều.

DH = DE => tam giác DEH là tam giác cân tại D.

EG = GF => tam giác GEF là tam giác cân tại G.

EH = EF (theo giả thiết) => tam giác EHF cân tại E.

c) IG = IH (theo giả thiết) => tam giác IGH cân tại I. Vì góc GIH = 60° (theo giả thiết), nên tam giác IGH là tam giác đều.

EG = EH (theo giả thiết) => tam giác EGH cân tại E.

d) Trong tam giác MBC, tổng ba góc là: góc M + góc B + góc C = 180°

Từ đó: 71° + góc B + 38° = 180° => Góc B = 180° - 71° - 38° = 71°

Góc B = góc M (=71°) => ΔCBM cân tại C

Bài 2. Xét tam giác ONM cân tại O. Chọn điểm D trên cạnh OM và điểm E trên cạnh ON sao cho OD = OE

a) So sánh góc OND và góc OME

b) Gọi I là giao điểm của ND và ME. Chứng minh tam giác INM cân và giải thích lý do.

Giải

a) Tam giác ONM cân tại O (theo giả thiết)

Do đó: ON = OM và Góc ONM = Góc OMN

Xét ΔOND và ΔOME, ta có: ON = OM (theo giả thiết) và góc O chung

OD = OE (theo giả thiết)

=> ΔOND = ΔOME (c.g.c)

=> Góc OND = Góc OME (do các cặp cạnh tương ứng bằng nhau)

b) Trong tam giác ΔINM có:

Góc INM = góc ONM - góc OND = góc OMN - góc OME = góc IMN

Vì vậy: Tam giác INM cân tại I

Bài 3. Xem hình 16, với điều kiện ED = EF; EI là tia phân giác của góc DEF.

Chứng minh rằng: a) ΔEID = ΔEIF; b) ΔDIF là tam giác cân.

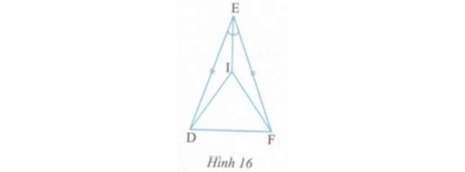
Giải:

a) Xem xét tam giác EID và EIF, chúng ta có:

+ ED = EF (theo giả thiết)

+ Góc IED = Góc EIF (do EI là tia phân giác của góc DEF)

+ EI là cạnh chung, nên: ΔEID = ΔEIF (c.g.c)

b) ΔEID = ΔEIF (theo chứng minh ở câu a) dẫn đến ID = IF, từ đó tam giác DIF cân tại I.

Bài 4. Xét tam giác ABC cân tại A, với các điểm E và F lần lượt nằm trên các cạnh AC và AB sao cho BE vuông góc với AC và CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.

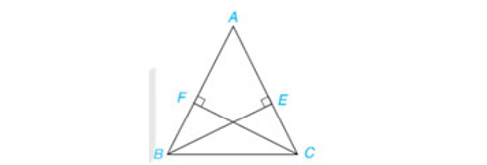
Đáp án gợi ý:

Vì tam giác ABC cân tại A nên: Góc ABC = Góc ACB (theo tính chất của tam giác cân)

Xem xét hai tam giác vuông BFC và CEB: Góc ABC = Góc ACB, BC là cạnh chung

=> ΔBFC = ΔCEB (cạnh huyền – góc nhọn)

=> BE = CF (hai cạnh tương ứng bằng nhau).

Bài 5. Tam giác vuông với hai cạnh góc vuông bằng nhau được gọi là tam giác vuông cân.

Giải thích các khẳng định sau đây:

a) Tam giác vuông cân thì có hai cạnh góc vuông bằng nhau và cân tại đỉnh góc vuông;

b) Tam giác vuông cân có hai góc nhọn đều bằng 45°;

Giải

a) Vì tổng ba góc trong một tam giác luôn bằng 180 độ, nên không thể có hai góc vuông trong cùng một tam giác.

=> Do đó, trong tam giác vuông cân, hai góc nhọn sẽ bằng nhau.

=> Tam giác vuông cân có đỉnh góc vuông là đỉnh cân của tam giác.

b) Gọi hai góc nhọn của tam giác vuông là x, ta có công thức:

x + x + 90 độ = 180 độ

=> 2x = 90 độ

=> x = 45 độ

Do đó, trong tam giác vuông cân, mỗi góc nhọn đều bằng 45°.

5. Phương pháp tính chu vi và diện tích của tam giác cân

- Để tính chu vi của một tam giác cân, bạn chỉ cần biết vị trí của đỉnh và độ dài của hai cạnh bằng nhau. Công thức tính sẽ như sau:

P = 2a + c

Công thức này bao gồm:

+ a: đại diện cho hai cạnh bên của tam giác

+ c: là cạnh đáy của tam giác.

- Diện tích của tam giác cân được tính bằng cách nhân chiều cao từ đỉnh xuống cạnh đáy, sau đó chia cho 2. Công thức tính diện tích tam giác cân như sau:

S = (a x h) / 2

Trong công thức này:

+ a: là độ dài của cạnh đáy tam giác cân (đáy là một trong ba cạnh của tam giác)

+ h: là chiều cao của tam giác (chiều cao là đoạn thẳng từ đỉnh xuống cạnh đáy).