| Hình tam giác | |
|---|---|
Hình tam giác | |
| Số cạnh và đỉnh | 3 |
| Ký hiệu Schläfli | {3} (đối với tam giác đều) |
| Diện tích | nhiều cách (xem bên dưới) |
| Góc ngoài (độ) | 60° (đối với tam giác đều) |
Tam giác hay còn gọi là hình tam giác là một dạng hình học cơ bản: một mặt phẳng hai chiều có ba đỉnh không nằm trên một đường thẳng và ba cạnh là ba đoạn thẳng nối các đỉnh lại với nhau. Đây là đa giác có số cạnh ít nhất (3 cạnh). Tam giác luôn là một đa giác đơn và cũng là một đa giác lồi (các góc trong luôn nhỏ hơn 180°). Một tam giác với các cạnh AB, BC và AC được ký hiệu là .
Ý nghĩa từ
Chữ Hán: 三角; nghĩa là 'ba góc'.
Các yếu tố cấu thành tam giác
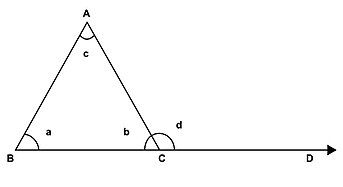
Các góc nằm bên trong một tam giác được gọi là góc trong, còn các góc kề bù với chúng được gọi là góc ngoài. Góc ngoài bằng tổng các góc trong không kề bù với nó. Mỗi tam giác có 3 góc trong và 6 góc ngoài.
Các đường đồng quy trong tam giác
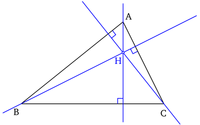
Đường cao là đoạn thẳng nối một đỉnh với cạnh đối diện và vuông góc với cạnh đó. Một tam giác có ba đường cao, và chúng đồng quy tại một điểm gọi là trực tâm của tam giác. Đường cao của tam giác vuông đi qua đỉnh góc vuông sẽ chia tam giác thành hai tam giác đồng dạng với nhau và với tam giác ban đầu.
Đường trung tuyến là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến, và chúng đồng quy tại một điểm gọi là trọng tâm. Khoảng cách từ trọng tâm đến mỗi đỉnh bằng của đường trung tuyến tương ứng, và khoảng cách từ trọng tâm đến mỗi trung điểm là của đường trung tuyến tương ứng. Đường thẳng đi qua bất kỳ đỉnh và trọng tâm của tam giác sẽ chia tam giác thành hai phần có diện tích bằng nhau. Trong mỗi tam giác, ba đường trung tuyến chia nó thành 6 tam giác có diện tích bằng nhau.
Đường trung trực của một tam giác là đường vuông góc với một cạnh tại trung điểm của cạnh đó. Tam giác có ba đường trung trực, và chúng đồng quy tại một điểm gọi là tâm của đường tròn ngoại tiếp tam giác. Tâm của đường tròn ngoại tiếp là điểm cách đều ba đỉnh của tam giác.
Đường phân giác là đoạn thẳng nối từ một đỉnh đến cạnh đối diện, chia góc ở đỉnh thành hai góc bằng nhau. Mỗi tam giác có ba đường phân giác, và chúng đồng quy tại một điểm gọi là tâm của đường tròn nội tiếp. Khoảng cách từ tâm của đường tròn nội tiếp đến các cạnh của tam giác là bằng nhau. Đường phân giác chia cạnh đối diện theo tỉ lệ với các cạnh còn lại của tam giác.
Theo định lý Euler: Trong một tam giác: trực tâm, trọng tâm và tâm của đường tròn ngoại tiếp tam giác đều nằm trên một đường thẳng, với trọng tâm nằm giữa trực tâm và tâm của đường tròn ngoại tiếp. Khoảng cách từ trực tâm đến tâm của đường tròn ngoại tiếp gấp ba lần khoảng cách từ trọng tâm đến tâm của đường tròn ngoại tiếp. Đường thẳng chứa ba điểm này được gọi là đường thẳng Euler.
- Về các đường đồng quy trong tam giác (như đường cao, đường trung tuyến, đường trung trực, đường phân giác), ta có thể nhận thấy như sau:
- Trọng tâm và tâm của đường tròn nội tiếp luôn nằm trong tam giác.
- Trực tâm nằm ngoài tam giác nếu là tam giác tù, trùng với đỉnh góc vuông nếu là tam giác vuông, và nằm bên trong nếu là tam giác nhọn.
- Tâm của đường tròn ngoại tiếp tam giác nằm ngoài tam giác nếu là tam giác tù, trùng với trung điểm của cạnh huyền nếu là tam giác vuông, và nằm bên trong nếu là tam giác nhọn.
- Trong tam giác cân: trực tâm, trọng tâm, tâm của đường tròn ngoại tiếp và tâm của đường tròn nội tiếp sẽ thẳng hàng, và đường thẳng này cũng chính là đường trung tuyến, đồng thời là đường phân giác, đường trung trực và đường cao tương ứng với cạnh đáy.
- Trong tam giác đều: trực tâm, trọng tâm, tâm của đường tròn ngoại tiếp và tâm của đường tròn nội tiếp trùng nhau, và các cặp đường trung tuyến, đường phân giác, đường trung trực, đường cao cũng trùng nhau.
- Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm của hai cạnh, song song với cạnh thứ ba và bằng một nửa chiều dài của cạnh đó.
Sự tương đồng giữa các tam giác
Hai tam giác được coi là bằng nhau khi có thể đặt trùng khít lên nhau qua các phép tịnh tiến, quay và đối xứng. Nói cách khác, hai tam giác là bằng nhau nếu tất cả các cạnh tương ứng và các góc tương ứng đều bằng nhau. Hai tam giác được xác định là bằng nhau khi và chỉ khi chúng thỏa mãn một trong các điều kiện sau đây:
- Hai tam giác có ba cặp cạnh tương ứng bằng nhau thì chúng bằng nhau (cạnh-cạnh-cạnh).
- Hai tam giác có hai cặp cạnh tương ứng bằng nhau và góc xen giữa các cạnh đó bằng nhau thì chúng bằng nhau (cạnh-góc-cạnh).
- Hai tam giác có một cặp cạnh tương ứng bằng nhau và hai cặp góc kề với cạnh đó bằng nhau thì chúng bằng nhau (góc-cạnh-góc).
- Hai tam giác vuông có một cặp cạnh huyền và một cặp cạnh góc vuông bằng nhau thì chúng bằng nhau (cạnh huyền-cạnh góc vuông).
- Hai tam giác vuông có một cặp cạnh huyền và một cặp góc nhọn bằng nhau thì chúng bằng nhau (cạnh huyền-góc nhọn).
- Hai tam giác vuông có hai cặp cạnh góc vuông bằng nhau thì chúng bằng nhau (cạnh góc vuông-cạnh góc vuông).
- Hai tam giác vuông có một cặp cạnh góc vuông và góc nhọn kề với nó bằng nhau thì chúng bằng nhau (cạnh góc vuông-góc nhọn).
- Quan hệ bằng nhau giữa các tam giác là trường hợp đặc biệt của quan hệ đồng dạng khi các cạnh tỷ lệ với hệ số tỷ lệ bằng 1.
Sự đồng dạng giữa các tam giác
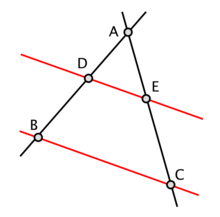
Hai tam giác được gọi là đồng dạng nếu một tam giác có thể biến đổi thành tam giác kia qua một phép vị tự. Các điều kiện cần và đủ để hai tam giác đồng dạng là:
- Hai tam giác có ba cặp cạnh tương ứng tỉ lệ với nhau thì chúng đồng dạng (cạnh-cạnh-cạnh).
- Hai tam giác có hai cặp góc tương ứng bằng nhau thì chúng đồng dạng (góc-góc).
- Hai tam giác có hai cặp cạnh tương ứng tỉ lệ và góc xen giữa hai cặp cạnh đó bằng nhau thì chúng đồng dạng (cạnh-góc-cạnh).
- Hai tam giác vuông có cặp cạnh huyền và một cặp cạnh góc vuông tương ứng tỉ lệ thì chúng đồng dạng (cạnh huyền-cạnh góc vuông).
- Hai tam giác bằng nhau thì cũng đồng dạng.
Các đặc điểm của tam giác đồng dạng:
Tỉ số đồng dạng giữa hai tam giác là tỷ lệ giữa các cặp cạnh tương ứng của hai tam giác khi chúng đồng dạng.
- Tỉ số giữa hai đường phân giác, hai đường cao, hai đường trung tuyến, hai đường tròn ngoại tiếp, hai đường tròn nội tiếp, và hai chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương của tỉ số đồng dạng.
Phân loại các tam giác
Trong hình học Euclid, khái niệm 'tam giác' thường chỉ những tam giác nằm trên một mặt phẳng. Tuy nhiên, còn tồn tại tam giác cầu trong hình học cầu và tam giác hyperbol trong hình học hyperbol. Tam giác phẳng có một số dạng đặc biệt, được phân loại theo các đặc điểm của các cạnh và các góc của nó:
Phân loại theo độ dài các cạnh
- Tam giác thường là loại tam giác cơ bản nhất với ba cạnh có độ dài khác nhau và ba góc nội khác nhau. Tam giác thường cũng bao gồm một số trường hợp đặc biệt của tam giác.
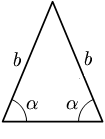
- Tam giác cân có hai cạnh bằng nhau, gọi là hai cạnh bên. Điểm giao của hai cạnh bên gọi là đỉnh của tam giác cân. Góc tại đỉnh gọi là góc đỉnh, còn hai góc còn lại gọi là góc đáy. Trong tam giác cân, hai góc đáy luôn bằng nhau.
- Tam giác đều là một dạng đặc biệt của tam giác cân, trong đó cả ba cạnh đều bằng nhau. Tam giác đều có ba góc bằng nhau, mỗi góc đều bằng 60°.
Phân loại theo số đo các góc nội tại
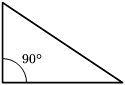
- Tam giác vuông là loại tam giác có một góc là 90° (góc vuông). Cạnh đối diện góc vuông được gọi là cạnh huyền và là cạnh dài nhất của tam giác. Hai cạnh còn lại gọi là cạnh góc vuông. Định lý Pythagoras, nổi tiếng với tam giác vuông, được đặt theo tên nhà toán học Pythagoras.
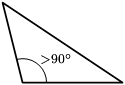
- Tam giác tù là tam giác có một góc lớn hơn 90° (góc tù) hoặc có một góc ngoài nhỏ hơn 90° (góc nhọn).
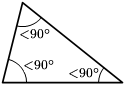
- Tam giác nhọn là tam giác có tất cả ba góc nội tại đều nhỏ hơn 90° (ba góc nhọn) hoặc tất cả góc ngoài đều lớn hơn 90° (sáu góc tù).
- Tam giác vuông cân là một dạng đặc biệt của tam giác, vừa là tam giác vuông, vừa là tam giác cân. Trong tam giác vuông cân, hai cạnh góc vuông có độ dài bằng nhau, và mỗi góc nhọn đều bằng 45°.
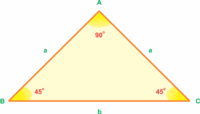
Các tính chất nổi bật của tam giác trong hình học Euclid
- Tổng các góc trong của một tam giác luôn luôn bằng 180° (định lý tổng góc trong của tam giác).
- Độ dài của mỗi cạnh trong tam giác luôn lớn hơn hiệu của hai cạnh còn lại và nhỏ hơn tổng của chúng (bất đẳng thức tam giác).
- Cạnh đối diện với góc lớn hơn sẽ dài hơn; ngược lại, góc đối diện với cạnh dài hơn sẽ lớn hơn (mối quan hệ giữa cạnh và góc đối diện).
- Ba đường cao của tam giác giao nhau tại một điểm gọi là trực tâm của tam giác (đồng quy tam giác).
- Ba đường trung tuyến của tam giác cắt nhau tại một điểm, được gọi là trọng tâm. Khoảng cách từ trọng tâm đến ba đỉnh của tam giác bằng 2/3 chiều dài của đường trung tuyến ứng với mỗi đỉnh. Đường trung tuyến chia tam giác thành hai phần có diện tích bằng nhau (đồng quy tam giác).
- Ba đường trung trực của tam giác cắt nhau tại một điểm, gọi là tâm của đường tròn ngoại tiếp tam giác (đồng quy tam giác).
- Ba đường phân giác của tam giác giao nhau tại một điểm, gọi là tâm của đường tròn nội tiếp tam giác (đồng quy tam giác).
- Định lý hàm số cosin: Trong tam giác, bình phương độ dài một cạnh bằng tổng bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh ấy với cosin của góc giữa chúng.
- Định lý hàm số sin: Trong tam giác, tỷ lệ giữa độ dài của mỗi cạnh và sin của góc đối diện là giống nhau cho tất cả các cạnh.
- Đường trung bình là đoạn thẳng nối hai trung điểm của hai cạnh trong tam giác; mỗi tam giác có ba đường trung bình. Đường trung bình song song với cạnh thứ ba và dài bằng một nửa cạnh đó. Tam giác được tạo bởi ba đường trung bình đồng dạng với tam giác ban đầu.
- Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỷ lệ với hai cạnh kề với góc đó.
Trong hình học phi Euclid, tổng ba góc của tam giác có thể thay đổi theo kích thước của tam giác. Khi kích thước tam giác tăng lên, tổng ba góc tiến gần tới giá trị 0 và diện tích trở nên vô hạn.

Các công thức tính diện tích của tam giác
Tính diện tích của tam giác là một trong những bài toán cơ bản thường xuất hiện trong hình học sơ cấp.
Áp dụng phương pháp hình học
Diện tích S được tính bằng ½bh, trong đó b là độ dài một cạnh bất kỳ của tam giác (gọi là đáy) và h là chiều cao hạ từ đỉnh đối diện xuống cạnh đáy.
Công thức này có thể được giải thích qua diện tích của hình chữ nhật như sau:
Từ một tam giác màu xanh lục, ta sao chép một tam giác tương tự (màu xanh lam), xoay góc 180°, và ghép chúng lại thành một hình bình hành. Khi cắt một phần của hình bình hành và ghép lại thành hình chữ nhật, ta có diện tích hình chữ nhật là bh, từ đó diện tích tam giác sẽ là ½bh.
Tương tự, diện tích của tam giác bằng tích của chiều dài đáy và chiều cao chia đôi:
- Đặc biệt
- Với tam giác vuông, diện tích tính bằng một nửa tích của hai cạnh góc vuông hoặc nửa tích của đường cao với cạnh huyền.
- Với tam giác đều, diện tích tính bằng bình phương độ dài một cạnh nhân với
Áp dụng phương pháp vectơ
Nếu tứ giác ABDC là hình bình hành thì diện tích của nó được tính bởi công thức: trong đó là tích có hướng của hai vectơ và . Diện tích tam giác ABC bằng một nửa diện tích của hình bình hành ABDC nên: |
Áp dụng phương pháp lượng giác
Diện tích tam giác có thể tính bằng nửa tích của độ dài hai cạnh và sin của góc giữa chúng.
|
Áp dụng phương pháp tọa độ
Khi đỉnh A được đặt tại gốc tọa độ (0, 0) trong hệ tọa độ Descartes, và các tọa độ của hai đỉnh còn lại là B = (xB, yB) và C = (xC, yC), thì diện tích S của tam giác ABC được tính bằng nửa giá trị tuyệt đối của định thức sau đây
Trong trường hợp tổng quát, công thức diện tích sẽ được áp dụng như sau:
Trong không gian ba chiều, diện tích của tam giác với các đỉnh {A = (xA, yA, zA), B = (xB, yB, zB) và C = (xC, yC, zC)} được tính bằng tổng các diện tích của các hình chiếu của nó lên các mặt phẳng tọa độ (tức là x=0, y=0 và z=0).
Áp dụng công thức Heron để tính diện tích tam giác
Diện tích của tam giác có thể được tính bằng công thức Heron:
Trong đó là nửa chu vi của tam giác.
Thông qua việc sử dụng đường tròn nội tiếp
Ký hiệu r là bán kính của đường tròn nội tiếp tam giác. Khi đó, là nửa chu vi của tam giác. Khi đó, diện tích
Thông qua đường tròn ngoại tiếp của tam giác
Ký hiệu R là bán kính của đường tròn ngoại tiếp tam giác. Khi đó, diện tích
Những nguyên tắc cơ bản về tam giác
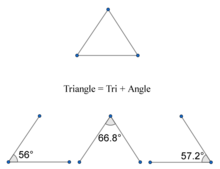
Euclid đã trình bày các nguyên lý cơ bản về tam giác trong các tập từ 1 đến 4 của tác phẩm Cơ sở (Elements), viết vào khoảng năm 300 TCN.
Tam giác là một loại đa giác, cụ thể là một hình đa diện bậc hai (xem thêm về đa diện).
Hai tam giác được gọi là đồng dạng nếu có thể biến đổi (co giãn) một tam giác thành tam giác còn lại theo cùng một tỷ lệ. Khi đó, tỷ lệ giữa các cạnh tương ứng của hai tam giác là như nhau. Nếu cạnh lớn nhất của tam giác này gấp n lần cạnh lớn nhất của tam giác kia, thì cạnh nhỏ nhất của tam giác này cũng gấp n lần cạnh nhỏ nhất của tam giác kia, và tương tự đối với các cạnh khác.
Ngoài ra, tỷ lệ giữa cạnh dài và cạnh ngắn của một tam giác phải giống như tỷ lệ giữa cạnh dài và cạnh ngắn của tam giác kia. Điều quan trọng là các góc tương ứng phải bằng nhau để đảm bảo sự đồng dạng giữa hai tam giác. Điều này cũng xảy ra khi hai tam giác có một cạnh chung và các cạnh còn lại của chúng bằng nhau.
Các hàm lượng giác sin và cosin có thể được hiểu qua việc sử dụng tam giác vuông và khái niệm đồng dạng. Đây là hai hàm góc quan trọng trong lượng giác học.
Các định lý nổi tiếng thường được áp dụng trong tam giác
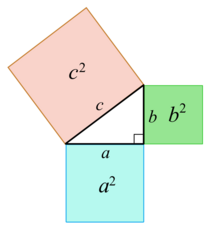
Một số định lý nổi tiếng liên quan đến tam giác bao gồm:
- Định lý Pythagoras: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. Công thức được viết như sau: c² = a² + b²
- Định lý Apollonius: Đối với tam giác ABC và đường trung tuyến AD, có công thức: AB² + AC² = 2(AD² + BD²)
- Định lý Stewart: Gọi a, b, và c lần lượt là các cạnh của tam giác, và d là độ dài của đoạn thẳng nối từ một đỉnh của tam giác đến một điểm trên cạnh đối diện (cạnh có độ dài a). Đoạn thẳng chia cạnh a thành hai đoạn có độ dài m và n. Định lý Stewart cho công thức: bm² + cn² = a(d² + mn)
- Định lý Thales: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại, thì các đoạn thẳng trên hai cạnh bị cắt sẽ tỷ lệ với nhau.
Ứng dụng của tam giác trong kiến trúc

Ngày nay, hình chữ nhật là hình dạng phổ biến nhất trong các công trình xây dựng nhờ vào khả năng xếp chồng và sắp xếp dễ dàng. Điều này cũng giúp thiết kế nội thất dễ dàng hơn. Tuy nhiên, hình tam giác, mặc dù khó sử dụng hơn về mặt lý thuyết, lại mang lại nhiều lợi ích đáng kể. Khi công nghệ máy tính hỗ trợ các kiến trúc sư trong việc thiết kế các công trình sáng tạo, hình dạng tam giác ngày càng được ưa chuộng trong các dự án xây dựng, đặc biệt là trong các tòa nhà cao tầng và các vật liệu xây dựng. Vào năm 1989 tại Tokyo, Nhật Bản, các kiến trúc sư đã thử thách với ý tưởng xây dựng một tòa tháp hơn 500 tầng để đáp ứng nhu cầu văn phòng ở thành phố đông đúc. Do lo ngại về động đất, họ đã chọn hình dạng tam giác cho tòa nhà.
Ở thành phố New York, trên các đại lộ lớn, bạn sẽ thấy nhiều công trình có hình dạng lăng trụ đứng với đáy tam giác. Ví dụ nổi bật là Tòa nhà Flatiron, mặc dù không gian bên trong không thuận tiện cho việc bố trí nội thất hiện đại, nhưng công trình này vẫn trở thành biểu tượng nổi bật. Các nhà thiết kế ở Na Uy cũng đã ứng dụng hình tam giác vào các công trình của họ. Hình dạng tam giác không chỉ xuất hiện trong các nhà thờ và tòa nhà công cộng mà còn trong các trường đại học và thiết kế nhà sáng tạo.
Cấu trúc của tam giác rất ổn định, trong khi cấu trúc của các đa giác khác có thể bị biến dạng dưới áp lực (ví dụ, hình chữ nhật có thể bị biến thành hình bình hành). Tam giác có khả năng tự nhiên để chống lại áp lực bên ngoài. Một tam giác sẽ giữ nguyên hình dạng trừ khi các cạnh của nó bị uốn cong, kéo dài hoặc gãy. Mỗi cạnh của tam giác hỗ trợ hai cạnh còn lại. Ngược lại, hình chữ nhật phụ thuộc nhiều hơn vào sức mạnh của các khớp nối. Các nhà thiết kế sáng tạo đang thử nghiệm với gạch không chỉ có hình chữ nhật mà còn hình tam giác để kết hợp theo ba chiều. Có khả năng cao rằng hình tam giác sẽ được sử dụng ngày càng nhiều trong các thiết kế phức tạp hơn. Mặc dù tam giác rất cứng cáp, nhưng khi sắp xếp không mạnh mẽ bằng hình lục giác trong tự nhiên.
- Tam giác Heron
- Tam giác cầu
- Tam giác tỷ lệ vàng
- Tam giác Bermuda
- Bất đẳng thức Pedoe
- Bất đẳng thức tam giác
