1. Gia tốc là gì?
Gia tốc là đại lượng đo lường sự thay đổi của vận tốc theo thời gian. Nói một cách khác, gia tốc biểu thị mức độ thay đổi vận tốc trong quá trình di chuyển. Nếu vận tốc không thay đổi, nghĩa là không có gia tốc. Gia tốc chỉ xuất hiện khi vận tốc thay đổi. Trong hệ đơn vị quốc tế SI, gia tốc được đo bằng m/s², tức là mét trên giây bình phương.
Gia tốc, một cách đơn giản, là đại lượng vật lý thể hiện sự thay đổi nhanh chóng hay chậm chạp của vận tốc, bao gồm cả hướng và độ lớn. Vận tốc và gia tốc đều là đại lượng véc tơ. Qua giá trị gia tốc, bạn có thể biết được sự thay đổi tốc độ của vật thể là nhanh hay chậm. Gia tốc đóng vai trò quan trọng trong vật lý, giúp mô tả chuyển động của các vật thể trong không gian và thời gian.
Chuyển động sẽ tăng tốc khi vectơ gia tốc cùng hướng với chuyển động, giảm tốc khi vectơ gia tốc ngược chiều với chuyển động, và thay đổi hướng khi vectơ gia tốc có hướng khác với chuyển động.
Ví dụ: Nếu bạn đang lái xe và đạp mạnh chân ga, xe sẽ có gia tốc dương (dương vì tốc độ tăng). Ngược lại, nếu bạn đạp mạnh chân phanh, xe sẽ có gia tốc âm (âm vì tốc độ giảm).
Một số loại gia tốc phổ biến mà bạn thường gặp là:
- Gia tốc tức thời
- Gia tốc trung bình
- Gia tốc pháp tuyến
- Gia tốc tiếp tuyến
- Gia tốc toàn phần
- Gia tốc trọng trường
2. Các công thức liên quan đến việc tính toán gia tốc
- Công thức tổng quát để tính gia tốc:
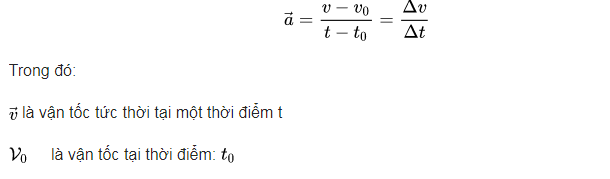
- Công thức tính gia tốc tức thời:
Gia tốc tức thời phản ánh sự thay đổi vận tốc của vật trong một khoảng thời gian rất ngắn (tức thời).
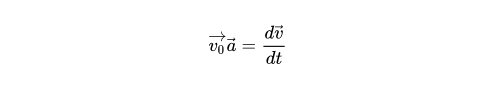
Trong đó:
v là vận tốc với đơn vị là m/s
t là thời gian với đơn vị là s
- Công thức tính gia tốc trung bình: Gia tốc trung bình thể hiện sự thay đổi vận tốc của vật trong một khoảng thời gian cụ thể. Nó được tính bằng sự biến thiên của vận tốc chia cho sự thay đổi thời gian.
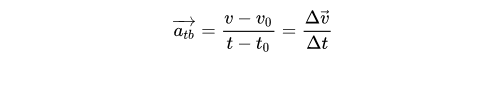
Trong đó:
v là tốc độ tức thời với đơn vị m/s
r là bán kính cong với đơn vị m
Lưu ý: Khi vật chuyển động theo đường tròn đều, v và R đều không thay đổi. Do đó, gia tốc pháp tuyến trong trường hợp này chính là gia tốc hướng tâm và là hằng số.
- Công thức tính gia tốc tiếp tuyến: Gia tốc tiếp tuyến đo sự thay đổi độ lớn của vectơ vận tốc. Gia tốc tiếp tuyến có phương trùng với phương của tiếp tuyến, cùng chiều với chuyển động khi vật tăng tốc và ngược chiều khi vật giảm tốc.
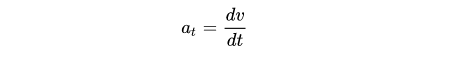
Mối liên hệ giữa gia tốc tiếp tuyến và gia tốc pháp tuyến. Gia tốc trong chuyển động theo đường cong gồm hai thành phần.
+ Gia tốc pháp tuyến: Đặc trưng cho sự thay đổi về phương của vận tốc theo thời gian
+ Gia tốc tiếp tuyến: Thể hiện sự thay đổi về hướng và độ lớn của vận tốc theo thời gian
- Công thức tính gia tốc toàn phần: Gia tốc toàn phần là tổng hợp của gia tốc tiếp tuyến và gia tốc pháp tuyến theo vectơ.
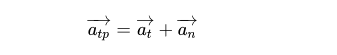
- Mối quan hệ giữa gia tốc, vận tốc và quãng đường.
Chúng ta sẽ chứng minh mối quan hệ giữa gia tốc, vận tốc và quãng đường như sau:
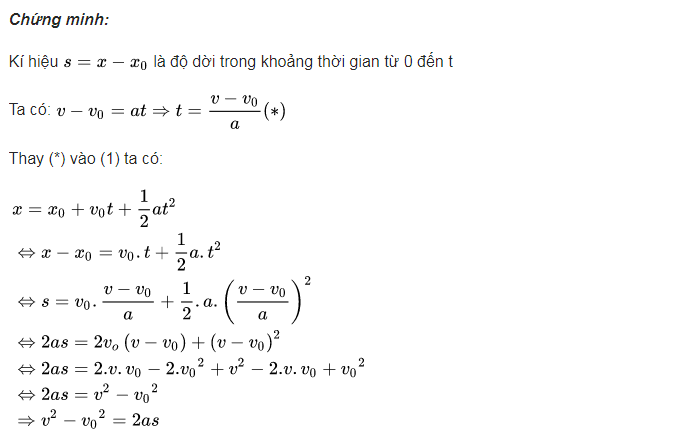
Để sử dụng công thức tính gia tốc giải bài tập vật lý, bạn có thể thực hiện các bước sau:
Bước 1: Xác định các thông số vận tốc và thời gian. Để tính gia tốc, bạn cần biết vận tốc và thời gian. Vận tốc có thể được cung cấp trong bài toán hoặc tính từ quãng đường và thời gian di chuyển. Thời gian cũng có thể có sẵn trong bài toán hoặc được tính từ các dữ liệu khác.
Bước 2: Áp dụng công thức tính gia tốc.
Sử dụng công thức gia tốc: a = (v - v0)/(t - t0) = Δv/Δt, trong đó a là gia tốc, v là vận tốc hiện tại, v0 là vận tốc ban đầu, t là thời gian hiện tại, t0 là thời gian ban đầu, Δv là sự thay đổi vận tốc và Δt là sự thay đổi thời gian. Từ các thông số đã xác định ở bước 1, bạn có thể tính gia tốc của vật.
Bước 3: Giải các bài tập vật lý liên quan đến gia tốc.
Dựa vào gia tốc đã tính, bạn có thể áp dụng để giải các bài tập vật lý liên quan, như tính lực tác động, khoảng cách di chuyển, hoặc tốc độ vật sau một khoảng thời gian. Đối với những bài tập phức tạp hơn, có thể cần sử dụng nhiều công thức và phương pháp khác nhau. Việc thực hành và nắm vững kiến thức cơ bản sẽ giúp bạn giải quyết các bài tập về gia tốc một cách chính xác và dễ dàng.
3. Các bài tập về gia tốc
1: Một chiếc xe tăng tốc từ 18,5 m/s lên 46,1 m/s trong khoảng thời gian 2,37 giây. Tính gia tốc trung bình của xe.
Viết công thức: a = Δv / Δt = (vf – vi)/(tf – ti)
Xác định các giá trị: vf = 46,1 m/s, vi = 18,5 m/s, tf = 2,47 s, ti = 0 s.
Tính toán: a = (46,1 – 18,5)/2,47 = 11,17 m/s².
2: Vật di chuyển theo hướng dương của trục Ox với vận tốc không thay đổi.
A. Tọa độ của vật luôn có giá trị dương.
B. Vận tốc của vật luôn mang giá trị dương.
C. Cả tọa độ và vận tốc của vật đều luôn có giá trị dương.
D. Tọa độ luôn trùng khớp với quãng đường di chuyển.
Đáp án đúng: B. Vận tốc của vật luôn có giá trị dương.
3: Xe di chuyển quãng đường 48 km trong thời gian t giây. Trong 1/4 thời gian đầu, xe chạy với tốc độ trung bình là v1 = 30 km/h. Tìm tốc độ trung bình trong phần thời gian còn lại:
A. 56 km/h.
B. 50 km/h.
C. 52 km/h.
D. 54 km/h.
Đáp án đúng: D. 54 km/h.
Hướng dẫn giải:
Quãng đường xe di chuyển từ A đến B là: s = 48t.
Quãng đường xe đã chạy trong 1/4 thời gian: s1 = 30.t/4
Tốc độ trung bình trong khoảng thời gian còn lại là:
Vtb = (48t - 7,5t)/0,75t = 54 km/h
4. Một vật được ném lên với vận tốc ban đầu 20 m/s và đạt đến độ cao 10 m. Tính thời gian vật đạt đến độ cao này và gia tốc của vật tại thời điểm đó.
Giải pháp:
Để tính thời gian đạt đến độ cao 10 m, sử dụng công thức: S = 1/2 x a x t^2
Trong đó,
S là quãng đường di chuyển, a là gia tốc, và t là thời gian.
10 = 1/2 x 9,8 x t^2
t = √(10/4,9) = 1,43 s
Thời gian để vật đạt độ cao 10 m là 1,43 s.
Gia tốc của vật tại thời điểm này có thể tính theo công thức:
a = v^2 / (2h)
Trong đó, v là vận tốc ban đầu của vật, và h là độ cao đạt được của vật.
a = 20^2 / (2 * 10) = 20 m/s²
Do đó, gia tốc của vật tại thời điểm đạt độ cao 10 m là 20 m/s².
Các bài tập vận dụng không có đáp án:
1. Một viên bi lăn từ đỉnh một mặt phẳng nghiêng với gia tốc 0,56 m/s²
a) Tính vận tốc của viên bi sau 2 giây kể từ khi bắt đầu chuyển động.
b) Sau bao lâu từ lúc bắt đầu lăn, viên bi đạt tốc độ 6,3 m/s? Tính quãng đường viên bi đi được từ lúc bắt đầu đến khi đạt tốc độ 6,6 m/s (giả sử mặt phẳng nghiêng đủ dài).
2. Một đoàn tàu đang di chuyển với vận tốc 45,2 km/h thì hãm phanh và chuyển động thẳng với gia tốc âm đến ga. Sau 2,5 phút, tàu dừng lại tại sân ga.
a) Tính toán gia tốc của đoàn tàu
b) Xác định quãng đường mà tàu đã di chuyển trong thời gian hãm
Tham khảo: Gia tốc là gì? Chuyển động nhanh dần đều có đặc điểm gì về gia tốc?
