| Thuật toán tìm kiếm cây và đồ thị |
|---|
|
| Danh sách |
|
| Liên quan |
|
Thuật toán Kruskal là phương pháp trong lý thuyết đồ thị dùng để tìm cây bao trùm có tổng trọng số nhỏ nhất cho một đồ thị liên thông không hướng có trọng số. Nói cách khác, thuật toán tìm một tập hợp các cạnh sao cho tạo thành cây chứa tất cả các đỉnh và có tổng trọng số các cạnh là tối thiểu. Đây là một ví dụ của thuật toán tham lam.
Thuật toán này được Joseph Kruskal giới thiệu lần đầu vào năm 1956.
Ngoài thuật toán Kruskal, một số phương pháp khác để giải quyết bài toán này là thuật toán Prim, thuật toán xóa ngược và thuật toán Borůvka.
Giới thiệu bài toán
Xét một đồ thị có trọng số với n đỉnh, nhiệm vụ là tìm cây khung nhỏ nhất.
Ý tưởng của thuật toán
Thuật toán Kruskal xây dựng cây khung nhỏ nhất dựa trên nguyên tắc hợp nhất các cạnh.
- Thuật toán không quan tâm đến thứ tự các cạnh.
- Thuật toán xử lý các cạnh theo thứ tự đã được sắp xếp theo trọng số.
Để tạo ra tập n-1 cạnh của cây khung nhỏ nhất - gọi là tập K, Kruskal đề xuất việc thêm từng cạnh vào tập này theo quy tắc như sau:
- Ưu tiên các cạnh có trọng số thấp hơn.
- Chỉ thêm cạnh vào tập khi nó không tạo thành chu trình với các cạnh đã có.
Nguyên tắc này đảm bảo chính xác và đáng tin cậy, với điều kiện tập K có đủ n - 1 cạnh sẽ tạo thành cây khung nhỏ nhất.
Chi tiết thuật toán
Để tìm cây bao trùm nhỏ nhất cho đồ thị G, thuật toán thực hiện các bước sau.
- Khởi tạo rừng F (tập hợp các cây), với mỗi đỉnh của G là một cây riêng lẻ.
- Khởi tạo tập S bao gồm tất cả các cạnh của G.
- Trong khi S chưa rỗng và F có hơn một cây:
- Xóa cạnh có trọng số nhỏ nhất từ S.
- Nếu cạnh này nối hai cây khác nhau trong F, thêm nó vào F và hợp nhất hai cây này.
- Nếu không, loại bỏ cạnh này.
Khi thuật toán hoàn tất, rừng sẽ chỉ còn lại một cây duy nhất, và đó chính là cây bao trùm nhỏ nhất của đồ thị G.
Thuật toán giả
Xét đồ thị G=(X, E).
Bước 1: Sắp xếp các cạnh của đồ thị theo thứ tự trọng số tăng dần.
Bước 2: Khởi tạo T:= Ø.
Bước 3: Xử lý từng cạnh trong danh sách đã sắp xếp. Nếu thêm cạnh vào T không tạo chu trình, cập nhật T:=T+{e}.
Bước 4: Nếu T đã có đủ n-1 cạnh thì dừng lại, nếu không thì tiếp tục từ bước 3.Phương pháp gán nhãn đỉnh
Kỹ thuật gán nhãn đỉnh Trong thuật toán Kruskal, để xác định xem T + {e} có tạo thành chu trình hay không, ta sử dụng kỹ thuật gán nhãn đỉnh, một phương pháp đơn giản và hiệu quả.
- Ngay sau bước 1 của thuật toán, mỗi đỉnh i của đồ thị sẽ được gán nhãn i.
- Trong bước 2:
- Nếu hai đầu của cạnh e có cùng nhãn (tức là nhãn của e.v1 và nhãn của e.v2 giống nhau), T+{e} sẽ tạo chu trình và ta không thêm e vào T.
- Ngược lại [nếu Label(e.v1) khác Label(e.v2)] ta sẽ đưa e vào T và cập nhật nhãn bằng cách:
- lab1 = Min(Label(e.v1), Label (e.v2))
- lab2 = Max(Label(e.v1), Label (e.v2))
- Thay đổi nhãn của tất cả các đỉnh có nhãn lab2 thành nhãn lab1.
Ghi chú
- Khi xây dựng T, các cạnh có thể chưa liên kết với nhau, lúc đó T chỉ là một rừng, chưa phải là cây khung.
- Khi thuật toán kết thúc:
- Nếu T chưa có đủ n - 1 cạnh, đồ thị G không liên thông (không có cây khung).
- Ngược lại, T là cây khung cần tìm.
Thời gian thực hiện
- Nếu E là số lượng cạnh và V là số lượng đỉnh của đồ thị, thì thuật toán Kruskal hoạt động trong thời gian O(E log V).
- Để đạt được thời gian này, ta sắp xếp tất cả các cạnh theo trọng số trong thời gian O(E log E). Việc này cho phép thực hiện bước 'xóa cạnh nhỏ nhất trong S' trong thời gian hằng số. Sau đó, sử dụng cấu trúc dữ liệu cho các tập hợp không giao nhau để quản lý thông tin về các đỉnh thuộc cây nào trong F. Ta cần thực hiện O(E) thao tác, bao gồm hai thao tác 'tìm' và không quá một thao tác 'hợp' cho mỗi cạnh. Ngay cả những thuật toán đơn giản như hợp bằng trọng số cũng có thể thực hiện O(E) thao tác trong thời gian O(E log V). Do đó, tổng thời gian là O(E log E) = O(E log V).
Chứng minh tính chính xác
Chứng minh bao gồm hai phần: xác nhận rằng kết quả của thuật toán là một cây bao trùm và rằng cây bao trùm này là nhỏ nhất.
Cây bao trùm
F luôn là một rừng vì việc nối hai cây bằng một cạnh luôn tạo ra một cây mới. Giả sử phản chứng rằng F có ít nhất hai cây A và B. Khi cạnh đầu tiên nối các đỉnh trong A của F với phần còn lại của đồ thị được xét đến (cạnh này tồn tại vì G liên thông), thuật toán sẽ chọn cạnh đó. Do đó, A không thể là một cây trong F khi thuật toán kết thúc. Vì vậy, F liên thông và chính là cây bao trùm.
Nhỏ nhất
Chúng ta sẽ chứng minh mệnh đề P bằng phương pháp quy nạp: Nếu F là tập hợp các cạnh đã được chọn tại bất kỳ thời điểm nào trong quá trình thực hiện thuật toán, thì luôn tồn tại một cây bao trùm nhỏ nhất chứa tập hợp F.
- Rõ ràng mệnh đề P đúng khi thuật toán bắt đầu vì lúc này F là tập rỗng.
- Giả sử mệnh đề P đúng với một tập hợp F và giả sử T là một cây bao trùm nhỏ nhất chứa F. Nếu cạnh tiếp theo được thêm vào là e nằm trong T, thì mệnh đề P vẫn đúng với F + e. Ngược lại, nếu T + e tạo thành một chu trình C, thì sẽ tồn tại một cạnh f nằm trên C mà không thuộc F. (Nếu không có cạnh f, thì e không thể được thêm vào F vì nó sẽ tạo chu trình C trong F.) Do đó, T − f + e là một cây và có trọng số bằng với T, vì T đã có trọng số nhỏ nhất và f không thể nhẹ hơn e, nếu không thuật toán đã chọn f trước e. Vì vậy, T − f + e là cây bao trùm nhỏ nhất chứa F + e và mệnh đề P là đúng.
- Vì thế, mệnh đề P đúng khi thuật toán kết thúc và F là một cây bao trùm. Điều này chỉ có thể xảy ra nếu F là cây bao trùm nhỏ nhất.
Ví dụ
- Giả sử đồ thị G như trong hình: Yêu cầu tìm cây bao trùm nhỏ nhất cho đồ thị G.
- Đồ thị G có 7 đỉnh
- Đồ thị G có n đỉnh. Thuật toán Kruskal sẽ dừng lại khi tập hợp T chứa n-1 cạnh
- n = 7
- Vậy số cạnh trong tập hợp T là: n - 1 = 7 - 1 = 6(*)
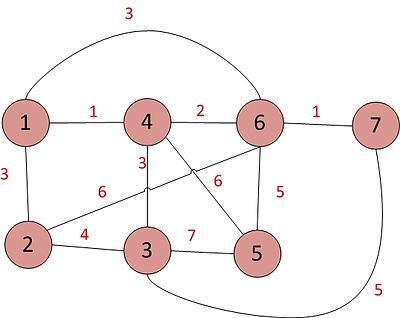
Bước 1: Liệt kê toàn bộ các cạnh và trọng số của chúng: Dựa vào đồ thị, ta liệt kê các cạnh kèm theo đỉnh đầu, đỉnh cuối và trọng số tương ứng.
| Điểm đầu | Điểm cuối | Trọng số |
|---|---|---|
| 1 | 2 | 3 |
| 1 | 4 | 1 |
| 1 | 6 | 3 |
| 2 | 3 | 4 |
| 2 | 6 | 6 |
| 3 | 4 | 3 |
| 3 | 5 | 7 |
| 3 | 7 | 5 |
| 4 | 5 | 6 |
| 4 | 6 | 2 |
| 5 | 6 | 5 |
| 6 | 7 | 1 |
Bước 2: Sắp xếp các cạnh theo thứ tự trọng số từ nhỏ đến lớn:
| Điểm đầu | Điểm cuối | Trọng số |
|---|---|---|
| 1 | 4 | 1 |
| 6 | 7 | 1 |
| 4 | 6 | 2 |
| 1 | 2 | 3 |
| 1 | 6 | 3 |
| 3 | 4 | 3 |
| 2 | 3 | 4 |
| 3 | 7 | 5 |
| 5 | 6 | 5 |
| 2 | 6 | 6 |
| 4 | 5 | 6 |
| 3 | 5 | 7 |
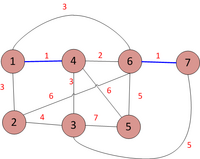
Bước 3: Sử dụng kết quả từ bước 2 để xác định cây khung bằng thuật toán Kruskal:






| Kết quả | Cạnh đang xét |
|---|---|
| 1-4-1: Ta nhận thấy cạnh 1-4 không tạo ra một chu trình nào. Vì vậy, thêm 1-4 vào tập hợp | |
| 6-7-1: Ta nhận thấy cạnh 6-7 không tạo ra một chu trình nào. Vì vậy, thêm 6-7 vào tập hợp | |
| 4-6-2: Ta nhận thấy cạnh 4-6 không tạo ra một chu trình nào. Vì vậy, thêm 4-6 vào tập hợp | |
| 1-2-3: Ta nhận thấy cạnh 1-2 không tạo ra một chu trình nào. Vì vậy, thêm 1-2 vào tập hợp | |
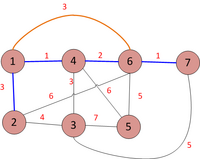
| 1-6-3: Ta nhận thấy cạnh 1-6 tạo ra một chu trình. Không thêm vào tập hợp.
3-4-3: Ta nhận thấy cạnh 3-4 không tạo ra một chu trình. Vì vậy, thêm 3-4 vào tập hợp | |
| 2-3-4: Ta nhận thấy cạnh 2-3 tạo ra một chu trình. Không thêm vào tập hợp. | |
| 3-7-5: Ta nhận thấy cạnh 3-7 tạo ra một chu trình. Không thêm vào tập hợp. | |
| 5-6-5: Ta nhận thấy cạnh 5-6 không tạo ra một chu trình nào. Vì vậy, thêm 5-6 vào tập hợp |
- Chúng ta đã thu thập được 6 cạnh. Kết thúc thuật toán. (Thỏa mãn điều kiện (*))
- Kết quả: Đồ thị sau khi xử lý như sau

Tổng chi phí: Cộng tất cả các trọng số của các cạnh lại với nhau
- Tổng chi phí tính được: 3 + 1 + 3 + 2 + 5 + 1 = 15
- Cây bao trùm tối ưu nhất
Ghi chú
- Kruskal, Joseph. B. (1956), “On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem”, Proceedings of the American Mathematical Society, 7 (1): 48–50
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (ấn bản 2). MIT Press và McGraw-Hill. ISBN 0-262-03293-7. Xem phần 23.2: Thuật toán Kruskal và Prim, trang 567–574.
- Goodrich, Michael T.; Tamassia, Roberto (2006). Data Structures and Algorithms in Java (ấn bản 4). John Wiley & Sons, Inc. ISBN 0-471-73884-0. Xem phần 13.7.1: Thuật toán Kruskal, trang 632.
Tài nguyên ngoài
- Hướng dẫn minh họa thuật toán Kruskal bằng ngôn ngữ Java
- Ví dụ lập trình thuật toán Kruskal bằng C#
