Thuật toán tìm kiếm A*

Trong khoa học máy tính, A* (đọc là A sao) là một thuật toán tìm kiếm trên đồ thị. Nó tìm đường từ một nút khởi đầu đến một nút đích (hoặc đến một nút thỏa mãn điều kiện đích). Thuật toán này sử dụng một 'đánh giá heuristic' để xếp loại các nút theo ước lượng về tuyến đường tốt nhất qua các nút đó, và duyệt các nút theo thứ tự của đánh giá này. Do đó, A* là một ví dụ của tìm kiếm theo lựa chọn tốt nhất (best-first search).

Thuật toán A* lần đầu được mô tả vào năm 1968 bởi Peter Hart, Nils Nilsson, và Bertram Raphael. Trong bài báo của họ, nó được gọi là thuật toán A; khi sử dụng với một đánh giá heuristic thích hợp sẽ đạt được hiệu suất tối ưu, do đó có tên A*.

Năm 1964, Nils Nilsson phát triển một phương pháp dựa trên khám phá để tăng tốc thuật toán Dijkstra, gọi là A1. Năm 1967, Bertram Raphael cải tiến đáng kể A1, nhưng không đạt được tối ưu, gọi là A2. Năm 1968, Peter E. Hart chứng minh A2 là tối ưu khi sử dụng đánh giá heuristic thích hợp. Ông gọi thuật toán mới này là A* (A sao, A-star).

Khái niệm trực quan

Xét bài toán tìm đường - một bài toán mà A* thường được sử dụng để giải quyết. A* dần dần xây dựng tất cả các tuyến đường từ điểm bắt đầu cho đến khi tìm được đường đến đích. Tuy nhiên, giống như tất cả các thuật toán tìm kiếm có thông tin (informed tìm kiếm thuật toán), nó chỉ xây dựng các tuyến đường có vẻ dẫn đến đích.

Để xác định tuyến đường nào có khả năng dẫn đến đích, A* sử dụng một 'đánh giá heuristic' về khoảng cách từ bất kỳ điểm nào đến đích. Trong bài toán tìm đường, đánh giá này có thể là khoảng cách đường chim bay - một ước lượng thường dùng cho khoảng cách trên đường.

Điểm khác biệt của A* với tìm kiếm theo lựa chọn tốt nhất là nó còn tính đến khoảng cách đã đi qua. Điều này làm cho A* 'đầy đủ' và 'tối ưu', nghĩa là, A* luôn tìm thấy đường đi ngắn nhất nếu có. A* không đảm bảo sẽ nhanh hơn các thuật toán tìm kiếm đơn giản hơn. Trong một mê cung, có thể cần đi xa đích trước khi quay lại để đến đích. Trong trường hợp này, thử các nút theo thứ tự 'gần đích hơn thì thử trước' có thể tốn thời gian.

Mô tả thuật toán

A* duy trì một tập các đường đi chưa hoàn thiện, bắt đầu từ nút xuất phát, trong một hàng đợi ưu tiên (priority queue). Thứ tự ưu tiên của một đường đi được quyết định bởi hàm f(x) = g(x) + h(x).

Trong đó, g(x) là chi phí của đường đi cho đến hiện tại, tức tổng trọng số của các cạnh đã đi qua. h(x) là hàm đánh giá heuristic về chi phí nhỏ nhất để đến đích từ x. Ví dụ, nếu 'chi phí' được tính bằng khoảng cách, thì khoảng cách đường chim bay giữa hai điểm là một đánh giá heuristic hợp lý.

Giá trị của hàm f(x) càng thấp thì độ ưu tiên của x càng cao (có thể dùng cấu trúc heap tối thiểu để cài đặt hàng đợi ưu tiên này).

function A*(điểm_bắt_đầu, đích)
    var đóng:= tập rỗng
    var q:= tạo_hàng_đợi(tạo_đường_đi(điểm_bắt_đầu))
    while q không rỗng
        var p:= lấy_phần_tử_đầu(q)
        var x:= nút cuối của p
        if x in đóng
            continue
        if x = đích
            return p
        thêm x vào tập đóng
        foreach y in các_đường_đi_tiếp_theo(p)
            thêm_vào_hàng_đợi(q, y)
    return thất_bại

Trong đó, các_đường_đi_tiếp_theo(p) trả về tập hợp các đường đi tạo bởi việc mở rộng p thêm một nút liền kề. Giả thiết rằng hàng đợi được sắp xếp tự động theo giá trị của hàm f.

'Tập đóng' (đóng) lưu tất cả các nút cuối của p (nơi các đường đi mới đã được mở rộng) để tránh lặp lại chu trình, dẫn đến thuật toán tìm kiếm theo đồ thị. Đôi khi hàng đợi được gọi là 'tập mở'. Tập đóng có thể bỏ qua (thu được thuật toán tìm kiếm theo cây) nếu đảm bảo có lời giải hoặc hàm các_đường_đi_tiếp_theo loại bỏ các chu trình.

Các tính chất

Giống như tìm kiếm theo chiều rộng (breadth-first search), A* là thuật toán hoàn chỉnh (complete) nghĩa là nó sẽ luôn tìm ra lời giải nếu tồn tại.

Nếu hàm heuristic h có tính chất thu nạp (admissible), tức không bao giờ đánh giá cao hơn chi phí thực sự nhỏ nhất để tới đích, thì A* có tính chất thu nạp (hay tối ưu) nếu sử dụng tập đóng. Nếu không dùng tập đóng, hàm h phải có tính chất đơn điệu (hay nhất quán) thì A* mới tối ưu. Nghĩa là nó không bao giờ đánh giá chi phí từ một nút đến nút kề cao hơn chi phí thực. Một cách hình thức, với mọi nút x và y (trong đó y là nút tiếp theo của x):

h(x) ≤ g(y) − g(x) + h(y)

A* có tính chất hiệu quả tối ưu (optimally efficient) với mọi hàm heuristic h, nghĩa là không có thuật toán nào dùng hàm heuristic đó mà mở ít nút hơn A*, trừ khi có một số lời giải chưa hoàn thiện mà tại đó h dự đoán chính xác chi phí đường đi tối ưu.

Bài toán ví dụ

Trên bàn cờ kích thước n x n, hãy tìm đường đi ngắn nhất từ điểm 〇 đến điểm △, với điều kiện:

• Các ô trắng là đường đi
• Các ô đen là vật cản, không đi được
• Chỉ được di chuyển lên, xuống, trái, phải nếu không bị cản. Không được đi chéo

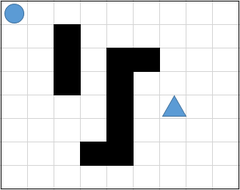
Trong bài toán này, đường đi ngắn nhất là đường chéo từ 〇 đến △

Chiều dài đường chéo được tính bằng công thức

Khi di chuyển qua mỗi ô, giá trị của ô sẽ tăng thêm 1 đơn vị

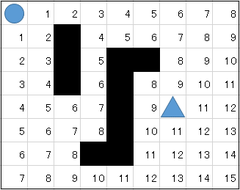
Vì f(x) = g(x) + h(x), ta có bảng sau:

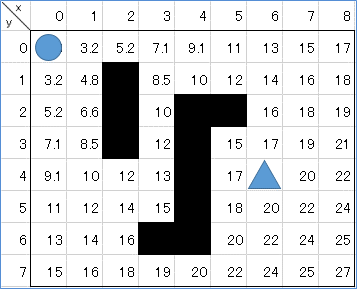
Tiếp theo từ vị trí 0 sẽ xét các ô xung quanh để tìm đường đi ngắn nhất

Ví dụ:

Xét điểm P(0,0), có 2 điểm kề bên là P(1,0) và P(0,1) với giá trị $f\left(x\right)=g\left(x\right)+h\left(x\right)=3.2$

Vì 2 giá trị bằng nhau nên chọn điểm nào cũng được. Ở bước 2 thì chọn điểm P(1,0)

Điểm P(1,0) có hai điểm liền kề với giá trị lần lượt là: $P(2,0)=5.2,P(1,1)=4.8$ cộng với điểm P(0,1) có sẵn, chúng ta có ba điểm $P(0,1)=3.2,P(2,0)=5.2,P(1,1)=4.8$

Theo mình, hàm đánh giá trong ví dụ trên tính sai. Việc so sánh giữa hai giá trị f(x) và h(x) là khác nhau nên so sánh này là không chính xác. Node cần di chuyển tới phải là node có giá trị hàm f(x) nhỏ nhất, không phải giá trị gần với f(x) của node đích (trong ví dụ là h(x) tại node đích là 8.6). Hãy tham khảo thêm tài liệu để tránh sai sót khi chỉ dựa trên Wikipedia. uet maidinh

Giá trị $P(2,0)=5.2$ là gần nhất với giá trị 8.6. Do đó, P(2,0) được chọn để xét tiếp. Tương tự các bước trước, chúng ta có bảng dưới đây.

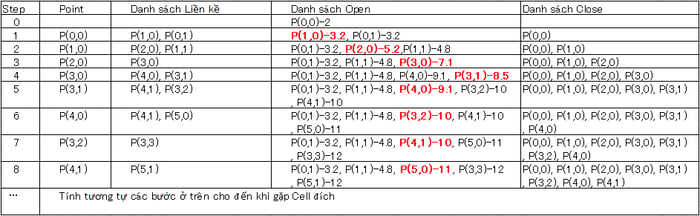
Sau khi đến được điểm △, ta có sơ đồ đường đi ngắn nhất như sau:

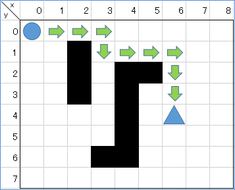
Liên hệ với tìm kiếm chi phí đều (uniform-cost search)

Thuật toán Dijkstra là một dạng đặc biệt của A* trong đó đánh giá heuristic là một hàm hằng $h\left(x\right)=0$ cho mọi $x$.

Độ phức tạp của thuật toán

Độ phức tạp thời gian của A* phụ thuộc vào đánh giá heuristic. Trong tình huống xấu nhất, số nút được mở rộng theo hàm mũ của độ dài lời giải, nhưng sẽ là hàm đa thức khi hàm heuristic h đáp ứng điều kiện sau:

$|h\left(x\right)-<!--\; -\; -->h^{\ast <!--\; \ast \; -->}\left(x\right)|\le <!--\; \le \; -->O(\log <!--\; \; -->h^{\ast <!--\; \ast \; -->}(x\left)\right)$

trong đó $h^{\ast <!--\; \ast \; -->}$ là heuristic tối ưu, tức là hàm cho ra chi phí chính xác để đi từ $x$ đến đích. Nói cách khác, sai số của h không nên tăng nhanh hơn logarit của 'heuristic hoàn hảo' $h^{\ast <!--\; \ast \; -->}$ - hàm cho biết khoảng cách thực từ x tới đích (Russell và Norvig 2003, tr. 101).

Vấn đề bộ nhớ của A* còn phức tạp hơn độ phức tạp thời gian. Trong trường hợp xấu nhất, A* phải lưu trữ số lượng nút tăng theo hàm mũ. Một số biến thể của A* đã được phát triển để giải quyết vấn đề này, bao gồm A* lặp sâu dần (iterative deepening A*), A* giới hạn bộ nhớ (memory-bounded A* - MA*) và A* giới hạn bộ nhớ đơn giản (simplified memory bounded A*).

Một thuật toán tìm kiếm có thông tin khác cũng tối ưu và đầy đủ nếu đánh giá heuristic của nó là có thể thu nạp được (admissible). Đó là tìm kiếm đệ quy lựa chọn tốt nhất (recursive best-first search - RBFS).

• Hart, P. E. (1968). Nilsson, N. J.; Raphael, B. “A Formal Basis for the Heuristic Determination of Minimum Cost Paths”. IEEE Transactions on Systems Science and Cybernetics SSC4 (2): 100–107.
• Hart, P. E. (1972). Nilsson, N. J.; Raphael, B. “Correction to 'A Formal Basis for the Heuristic Determination of Minimum Cost Paths'”. SIGART Newsletter. 37: 28–29.
• Nilsson, N. J. (1980). Principles of Artificial Intelligence. Palo Alto, California: Tioga Publishing Company.
• Russell, S. J. (2003). Artificial Intelligence: A Modern Approach. Norvig, P. tr. 97-104.

Liên kết ngoài

Ngôn ngữ: Tiếng Anh

• Hướng dẫn thuật toán A* của Justin Heyes-Jones tại đây
• Mô phỏng bước đơn tương tác của Herbert Glarner trong VB 6.0, được triển khai dưới dạng DLL, bao gồm giao diện người dùng cho phép mô phỏng trên lưới do người dùng định nghĩa.
• Một hướng dẫn khác về thuật toán A* cho người mới bắt đầu Lưu trữ 2005-12-24 tại Wayback Machine (chú ý: sai sót khi cho rằng A* luôn cần một 'tập đóng')
• Suy nghĩ của Amit về tìm đường và A*
• Minh họa của Sven Koenig về lập kế hoạch suốt đời A* và A*
• Bài viết của Tony Stentz về tìm đường D* (Dynamic A*) Lưu trữ 2006-09-12 tại Wayback Machine
• Bản demo JSearch của Remko Tronçon và Joost Vennekens Lưu trữ 2006-07-15 tại Wayback Machine: minh họa các thuật toán tìm kiếm khác nhau, bao gồm cả A*.
• Bài viết của Sune Trudslev về tìm đường trong C# Lưu trữ 2006-07-21 tại Wayback Machine