Tích trong toán học

Trong lĩnh vực toán học, tích chính là kết quả thu được từ phép nhân, hoặc một biểu thức thể hiện sự nhân giữa các yếu tố. Ví dụ, 6 là tích của 2 và 3 (kết quả của phép nhân), còn $x\cdot <!--\; \cdot \; -->(2+x)$ là tích của $x$ và $(2+x)$ (cho thấy hai nhân tố cần được nhân với nhau).

Thứ tự của các số thực hoặc số phức khi nhân không làm thay đổi kết quả; đặc điểm này được gọi là tính giao hoán. Tuy nhiên, khi nhân với ma trận hoặc các đối tượng đại số khác, thứ tự nhân có thể ảnh hưởng đến kết quả. Ví dụ, phép nhân ma trận và phép nhân trong các đại số khác thường không thỏa mãn tính giao hoán.

Trong toán học, có rất nhiều loại tích khác nhau: ngoài việc là phép nhân giữa các số, đa thức hoặc ma trận, còn có những phép nhân được định nghĩa trên nhiều cấu trúc đại số khác nhau. Một cái nhìn tổng quan về các loại tích này được trình bày ở đây.

Tích của hai số

Tích của hai số nguyên dương

Nếu đặt các viên đá vào trong một hình chữ nhật có $r$ hàng và $s$ cột, tổng số viên đá sẽ là

$r\cdot <!--\; \cdot \; -->s=\underset{i=1}{\overset{s}{\sum <!--\; \sum \; -->}}r=\underset{j=1}{\overset{r}{\sum <!--\; \sum \; -->}}s$

các viên đá.

Tích của hai số nguyên

Số nguyên bao gồm cả số dương và số âm. Khi nhân hai số nguyên, quy tắc thực hiện giống như với các số tự nhiên, nhưng cần lưu ý thêm quy tắc về dấu của kết quả:

Diễn đạt bằng lời:

• Âm nhân Âm bằng Dương
• Âm nhân Dương bằng Âm
• Dương nhân Âm bằng Âm
• Dương nhân Dương bằng Dương

Tích của hai phân số

Để nhân hai phân số, ta thực hiện phép nhân tử số với tử số và mẫu số với mẫu số:

Tích của hai số thực

Để có định nghĩa chính xác về tích của hai số thực, hãy tham khảo phần Xây dựng trường số thực.

Tích của hai số phức

Để nhân hai số phức, ta sử dụng quy tắc phân phối và định nghĩa $i^2=-<!--\; -\; -->1$:

Số phức có thể được biểu diễn trong hệ tọa độ cực như sau:

Thêm vào đó,

$c+di=s\cdot <!--\; \cdot \; -->(\cos <!--\; \; -->(\mathrm{\psi <!--\; \psi \; -->})+i\sin <!--\; \; -->(\mathrm{\psi <!--\; \psi \; -->}\left)\right)=s\cdot <!--\; \cdot \; -->e^{i\mathrm{\psi <!--\; \psi \; -->}}$, từ đó ta có:

Ý nghĩa hình học là chúng ta nhân các bán kính và cộng các góc.

Tích của hai quaternion

Tích của hai quaternion có thể được tìm hiểu chi tiết trong các tài liệu về quaternions. Tuy nhiên, cần lưu ý một điểm thú vị rằng $a\cdot <!--\; \cdot \; -->b$ và $b\cdot <!--\; \cdot \; -->a$ nói chung không bằng nhau.

Tích của dãy số

Ký hiệu đại diện cho tích của một dãy số là ký tự Hy Lạp viết hoa pi ∏ (tương tự như ký tự viết hoa Sigma ∑ dùng để biểu thị tổng). Tích của một dãy chỉ có một số duy nhất chính là số đó. Tích của một dãy rỗng được gọi là tích rỗng và có giá trị bằng 1.

Vành giao hoán

Vành giao hoán có một phép nhân duy nhất.

Các lớp dư trong số nguyên

Các lớp dư trong vành $Z/NZ$ có thể thực hiện phép cộng với nhau:

$(a+NZ)+(b+NZ)=a+b+NZ$

và cũng có thể thực hiện phép nhân với nhau:

$(a+NZ)\cdot <!--\; \cdot \; -->(b+NZ)=a\cdot <!--\; \cdot \; -->b+NZ$

Vành hàm số

Các hàm số thực có thể được cộng và nhân với nhau bằng cách thực hiện phép toán trên kết quả của chúng:

$(f+g)\left(m\right):=f\left(m\right)+g\left(m\right)$

$(f\cdot <!--\; \cdot \; -->g)\left(m\right):=f\left(m\right)\cdot <!--\; \cdot \; -->g\left(m\right)$

Tích chập

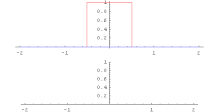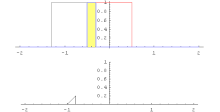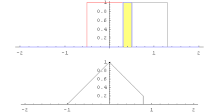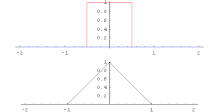
Hai hàm đồng hóa có thể được nhân với nhau qua một phương pháp đặc biệt gọi là tích chập.

Nếu

thì tích phân

$(f\ast <!--\; \ast \; -->g)\left(t\right):=\underset{-<!--\; -\; -->\mathrm{\infty <!--\; \infty \; -->}}{\overset{\mathrm{\infty <!--\; \infty \; -->}}{\int <!--\; \int \; -->}}f\left(\mathrm{\tau <!--\; \tau \; -->}\right)\cdot <!--\; \cdot \; -->g(t-<!--\; -\; -->\mathrm{\tau <!--\; \tau \; -->})d\mathrm{\tau <!--\; \tau \; -->}$

được xác định và gọi là tích chập.

Trong biến đổi Fourier, tích chập chuyển thành phép nhân điểm của hàm.

Vành đa thức

Tích của hai đa thức được định nghĩa như sau:

$\left(\underset{i=0}{\overset{n}{\sum <!--\; \sum \; -->}}{a}_i{X}^i\right)\cdot <!--\; \cdot \; -->\left(\underset{j=0}{\overset{m}{\sum <!--\; \sum \; -->}}{b}_j{X}^j\right)=\underset{k=0}{\overset{n+m}{\sum <!--\; \sum \; -->}}{c}_k{X}^k$

trong đó

$c_k=\underset{i+j=k}{\sum <!--\; \sum \; -->}{a}_i\cdot <!--\; \cdot \; -->b_j$

Tích trong đại số tuyến tính

Phép vô hướng

Theo định nghĩa trong không gian vector, ta có thể tính tích vô hướng giữa bất kỳ hai vector nào, thông qua ánh xạ $R\times <!--\; \times \; -->V\to <!--\; \to \; -->V$.

Tích vô hướng

Tích chéo trong không gian ba chiều

Tích của ánh xạ tuyến tính

Tích của hai ma trận

Tích của hàm tuyến tính tương tự như phép nhân ma trận

Tích Tensor trong không gian vector

Các lớp của mọi đối tượng với tích tensor

Các loại tích khác trong đại số tuyến tính

Tích Descartes

Tích không có nội dung

Tích trên các cấu trúc đại số khác nhau

Các loại tích trong lý thuyết phân loại

Các dạng tích khác

•  Tích Deligne tensor trong phân loại Abel

Các liên kết bên ngoài

• Định nghĩa trên Wolfram Mathworld
• “Product”. PlanetMath.