
Công thức tính diện tích tam giác đều là một phần kiến thức quan trọng trong toán học và thường được áp dụng rộng rãi. Trong bài viết này, chúng ta sẽ học cách tính diện tích tam giác đều và đường cao tam giác đều theo các công thức chuẩn nhất. Hãy cùng khám phá!
Công thức tính diện tích hình tam giác
Trước khi tìm hiểu cách tính diện tích tam giác đều, chúng ta sẽ điểm qua một số khái niệm cơ bản, tính chất và công thức tính diện tích hình tam giác:
Hình tam giác là gì?
Trong hình học, hình tam giác là một loại hình có 3 cạnh và 3 đỉnh. Các đỉnh không nằm trên cùng một đường thẳng và tổng của 3 góc trong tam giác luôn bằng 180 độ.

Công thức chung để tính diện tích hình tam giác
Để tính diện tích hình tam giác, chúng ta nhân chiều dài cạnh đáy với độ dài đường cao rồi chia cho 2. Công thức chính xác như sau:
S = ½ x (a x h)
Trong công thức này:
- a: độ dài cạnh đáy
- h: chiều cao từ đỉnh đối diện đến cạnh đáy, vuông góc với cạnh đáy của tam giác
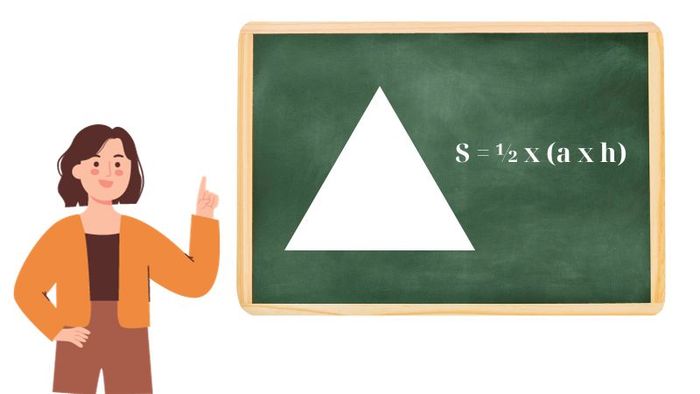
Lưu ý: Đây là công thức chung có thể áp dụng cho tất cả các loại hình tam giác, bao gồm cả tam giác đều.
Ví dụ: Cho tam giác ABC, với AH vuông góc với BC. Biết AH = 6m, BC = 7m. Tính diện tích tam giác ABC?
Hướng dẫn giải:
Diện tích tam giác ABC là: (6 x 7) / 2 = 42 / 2 = 21 (m2).
Vậy, diện tích tam giác ABC là 21 m2.
Phân biệt các loại tam giác trong hình học
Chú ý rằng, trong toán học có nhiều loại tam giác khác nhau và bạn có thể phân biệt để áp dụng cách tính diện tích tam giác đều, tam giác vuông… qua một số đặc điểm liên quan đến góc, cạnh, như:

- Tam giác thường: Không có góc vuông, không có cạnh hay góc nào bằng nhau.
- Tam giác tù: Có một góc lớn hơn 90 độ.
- Tam giác nhọn: Gồm ba góc bé hơn 90 độ.
- Tam giác vuông cân: Có một góc vuông và hai cạnh bằng nhau.
- Tam giác vuông: Một góc bằng 90 độ, hai cạnh góc vuông và cạnh huyền.
- Tam giác cân: Hai cạnh và hai góc bằng nhau, hai cạnh bằng nhau là cạnh bên và đáy.
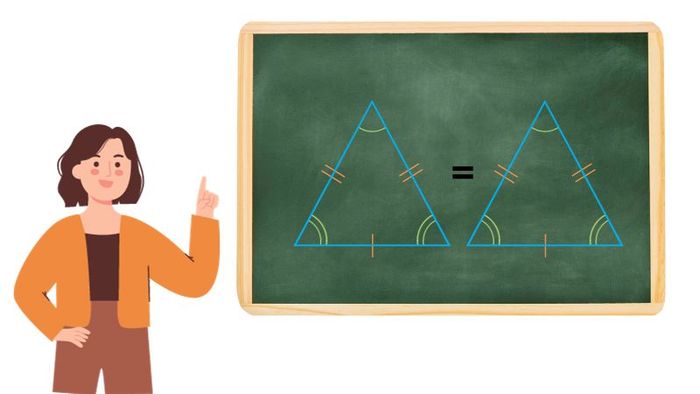
- Tam giác đều: Ba cạnh và ba góc bằng nhau (mỗi góc 60 độ). Áp dụng công thức và cách tính diện tích tam giác đều để nhanh chóng có kết quả.
Tính chất của tam giác
Dưới đây là những tính chất cơ bản khi giải bài toán có tam giác:
- Tam giác luôn có tổng của ba góc bằng 180 độ.
- Khi cộng hai cạnh của tam giác lại với nhau, ta sẽ được một con số lớn hơn so với cạnh thứ ba. Ví dụ, với ba cạnh a, b, c của tam giác, ta có a + c > b, b + c > a và a + b > c.
- Hai tam giác bằng nhau nếu các góc và các cạnh tương ứng của chúng bằng nhau.
- Mỗi tam giác đều có ba đường cao, mỗi đường cao kết nối từ đỉnh đến cạnh đối diện và vuông góc với cạnh đối diện.
- Mỗi tam giác đều có ba đường trung tuyến, mỗi đường trung tuyến kết nối từ một đỉnh đến trung điểm của cạnh đối diện.
Cách tính diện tích tam giác đều
Như đã đề cập ở trên, tam giác đều là một dạng đặc biệt của tam giác. Một tam giác được gọi là đều nếu có một trong số các đặc điểm sau:
- Tam giác có ba cạnh bằng nhau.
- Tam giác có ba góc bằng nhau và mỗi góc đều bằng 60 độ.
- Tam giác cân có hai cạnh bằng nhau và hai góc bằng 60 độ.
- Tam giác có hai góc bằng 60 độ được xem là tam giác đều.
Sau khi xác định đó là một hình tam giác đều, bạn có thể áp dụng các tính chất cơ bản sau:
- Ba góc bằng nhau và mỗi góc đều là 60 độ.
- Đường trung tuyến (đi qua trung điểm của cạnh đáy) trong tam giác đều đồng thời cũng là đường phân giác (chia một góc thành hai góc bằng nhau) và đường cao (vuông góc với cạnh đáy).
Dựa vào dữ liệu của bài toán, bạn có thể áp dụng từng công thức khác nhau như sau:
Trong trường hợp bài toán cung cấp chiều dài của một cạnh và chiều dài của đường cao.
Trong tình huống này, bạn có thể sử dụng công thức chung là: S = ½ x (a x h).

Ví dụ:
Tính diện tích tam giác đều ABC khi có đường cao là 12cm và chiều dài cạnh là 8cm:
=> Diện tích của tam giác ABC là: (8 x 12) / 2 = 48 (cm2).
Trong trường hợp bài toán chỉ cung cấp chiều dài của cạnh.
Nếu bạn chỉ biết chiều dài của cạnh, bạn có thể nối một đường từ đỉnh đến đáy để tạo thành đường cao. Đường cao này sẽ cắt cạnh đối diện tại trung điểm của cạnh đó. Sau đó, áp dụng công thức Pythagore (a2 + b2 = c2) để tính độ dài của đường cao và tiếp tục tính diện tích hình tam giác đều như trong trường hợp trước.
Hoặc, để tiết kiệm thời gian, bạn có thể sử dụng công thức tính nhanh sau:
S = (a^2 * √3) / 4

Tức là, chúng ta sẽ lấy bình phương chiều dài của cạnh tam giác đều nhân với √3 rồi chia cho 4 để tính diện tích hình tam giác đều.
Ví dụ:
Cho tam giác ABC có ba cạnh bằng nhau, mỗi cạnh độ dài 6cm, hãy tính diện tích tam giác này?
Tam giác ABC có ba cạnh bằng nhau, do đó là một tam giác đều. Áp dụng công thức trên, diện tích tam giác ABC là:
S = (6^2 * √3) / 4 = 15.6 (cm2).
Trong bài toán, yêu cầu tính độ dài của đường cao của tam giác đều.
Ngoài các phương pháp tính diện tích tam giác đều đã đề cập, trong một số trường hợp, bài toán cũng có thể yêu cầu tính chiều cao của tam giác đều.
Trước khi đi vào hướng dẫn chi tiết, bạn cần hiểu rõ tính chất của đường cao trong tam giác đều:
- Đường cao trong tam giác đều là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đáy và vuông góc với cạnh đáy.
- Trong tam giác đều, ba đường cao bằng nhau và cắt nhau tại một điểm duy nhất – đây là trọng tâm của tam giác, nơi các đường cao vuông góc với nhau.
- Đối với tam giác đều, bạn có thể tính chiều dài đường cao bằng công thức: h = a√3/2 (với a là độ dài cạnh của tam giác).
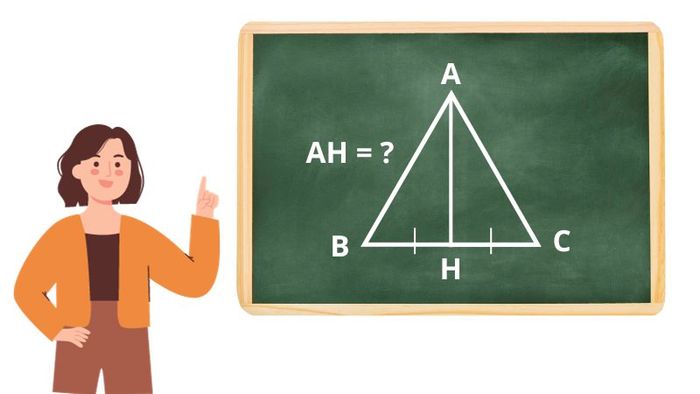
Ví dụ: Tính chiều dài đường cao AH của tam giác ABC, biết AB = 5cm?
Áp dụng công thức trên, ta có AH = AB√3/2 = 5√3/2 = 4.33 (cm).
Cách tính diện tích các loại tam giác khác
Ngoài cách tính diện tích tam giác đều, bạn cũng có thể sử dụng các công thức sau để tính diện tích của một số loại tam giác thông thường khác:
Cách tính diện tích tam giác cân
Với tam giác cân, có 2 cạnh bằng nhau và đường cao nối từ đỉnh xuống trung điểm của cạnh đáy. Công thức tính diện tích vẫn là:
S = ½ x (a x h)
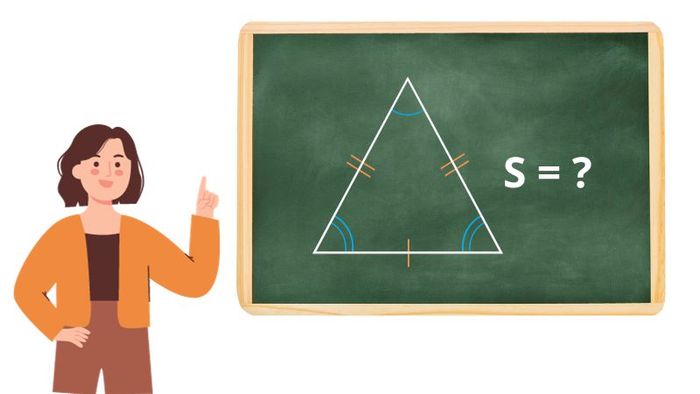
Trong đó, a là độ dài cạnh đáy và h là chiều cao.
Ví dụ: Tính diện tích tam giác cân ABC với cạnh đáy dài 10 cm và đường cao là 7 cm?
Diện tích tam giác ABC là: S = (a x h) / 2 = (10 x 7) / 2 = 35 (cm2).
Cách tính diện tích tam giác vuông
Với công thức S = ½ x (a x h), trong tam giác vuông, a và h là độ dài của 2 cạnh góc vuông, và hai cạnh này vuông góc với nhau. Bất kỳ cạnh nào làm cạnh đáy, cạnh còn lại được xem là đường cao.
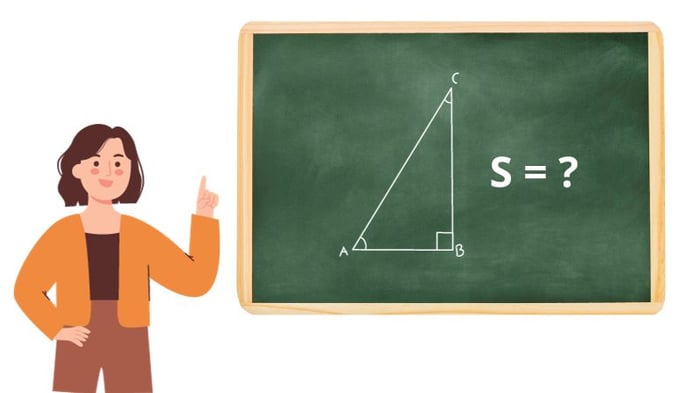
Ví dụ: Cho tam giác vuông ABC, với AB = 3m và BC = 4m, tính diện tích tam giác ABC.
Diện tích tam giác ABC là: (3 x 4) / 2 = 6 (m2).
Cách tính diện tích tam giác vuông cân
Giống như cách tính diện tích tam giác đều, tam giác vuông cân là một loại hình tam giác đặc biệt có 1 góc vuông và hai cạnh góc vuông bằng nhau. Các góc còn lại bằng nhau, mỗi góc là 45 độ.
Có thể dùng công thức tính nhanh sau:
S = a^2/2

Trong đó, a là độ dài cạnh đáy.
Ví dụ: Cho tam giác ABC vuông tại A, có AB = AC = 5cm. Tính diện tích tam giác ABC?
ABC vuông tại B và hai cạnh góc vuông bằng nhau (mỗi cạnh đều 5cm), nên đây là tam giác vuông cân.
Tính cạnh đáy BC (cạnh huyền của tam giác) bằng công thức Pitago: AB^2 + AC^2 = BC^2 => BC = √50.
Vậy diện tích tam giác ABC = BC^2/2 = 50/2 = 25 (cm).
Một số lưu ý quan trọng khi giải các bài toán tính diện tích tam giác
Để giải nhanh các bài toán về diện tích tam giác, bạn cần hiểu rõ một số điều sau:
Hiểu rõ tính chất của từng loại tam giác
Việc hiểu rõ tính chất giúp bạn dễ dàng nhận biết loại tam giác và áp dụng phương pháp tính diện tích thích hợp như tam giác đều hay tam giác vuông… để tiết kiệm thời gian và công sức. Đôi khi đề bài không cung cấp đủ dữ liệu, yêu cầu người giải phải áp dụng linh hoạt để đưa ra kết quả chính xác.
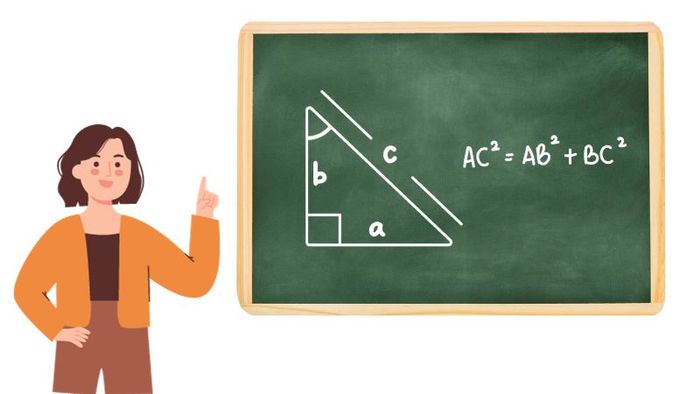
Áp dụng định lý Pitago
Khi giải các bài toán tam giác vuông, thường cần sử dụng định lý Pitago để tìm dữ kiện cần thiết. Hãy xem xét và áp dụng định lý này để giải bài toán một cách nhanh chóng và hiệu quả nhất!
Luyện tập thường xuyên
Để hiểu rõ cách tính diện tích tam giác đều và các loại tam giác khác, bạn cần luyện tập thường xuyên. Qua đó, bạn có thể nhận biết được các dạng đề thường gặp và áp dụng phương pháp giải phù hợp nhất. Bất kể trình độ toán học của bạn như thế nào, chỉ cần bạn chăm chỉ luyện tập, chắc chắn bạn sẽ giải được mọi loại bài toán tam giác một cách thành thạo.

Bài viết trên cung cấp cách tính diện tích tam giác đều và một số loại tam giác khác để bạn tham khảo. Hy vọng nó hữu ích và đừng quên chia sẻ để mọi người cùng biết nhé!
