Tính đối xứng qua trục

Trong không gian hai chiều hồng tâm có đối xứng trục.

Một mặt quay có đối xứng trục trong không gian 3 chiều.

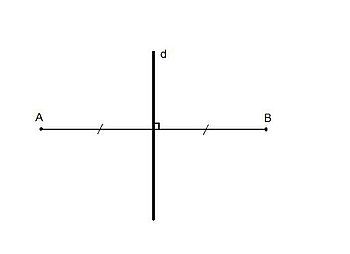
Khi đường thẳng d là đường trung trực của đoạn thẳng AB, ta nói điểm A đối xứng với điểm B qua đường thẳng d. Đường thẳng d

được gọi là trục đối xứng của điểm A và B.

Nói cách khác, hai điểm được gọi là đối xứng với nhau qua một đường thẳng nếu đường thẳng đó là đường trung trực của đoạn thẳng nối hai điểm đó. Đối xứng này được gọi là đối xứng trục.

Hai hình đối xứng qua một đường thẳng

Hai hình được coi là đối xứng với nhau qua một đường thẳng nếu mỗi điểm của hình này cách đều đường thẳng đó như điểm tương ứng trên hình kia, và ngược lại. Đây còn được gọi là đối xứng trục.

Trong mặt phẳng hai chiều, hình ảnh của một hình sau khi phản chiếu qua trục đối xứng với hình gốc, trong không gian ba chiều chúng đối xứng với nhau qua một mặt phẳng.

Hình có đối xứng qua trục.

Định nghĩa: cmmb

Một hình phẳng được coi là có đối xứng qua trục nếu tồn tại ít nhất một đường thẳng sao cho mỗi điểm trên hình đều có một điểm tương ứng với nó trên hình và nằm đối xứng qua đường thẳng đó. Nói cách khác, hình vẫn giữ nguyên khi phản chiếu qua đường thẳng này.

Trục đối xứng của một số hình học

1. Đường tròn, trục đối xứng là đường kính của đường tròn. Đường tròn có vô số trục đối xứng.
2. Tam giác cân, trục đối xứng là đường cao, đường trung tuyến, đường phân giác xuất phát từ đỉnh tương ứng với cạnh đáy. Tam giác cân chỉ có 1 trục đối xứng.
3. Tam giác đều, trục đối xứng là đường cao, đường trung trực, đường trung tuyến, đường phân giác của tam giác đều. Tam giác đều có 3 trục đối xứng.
4. Hình thang cân, trục đối xứng là đường thẳng qua trung điểm hai đáy của hình thang cân. Hình thang cân có 1 trục đối xứng.
5. Hình thoi, trục đối xứng là hai đường chéo của hình thoi. Hình thoi có 2 trục đối xứng.
6. Hình vuông, trục đối xứng là hai đường chéo của hình vuông và hai đường qua trung điểm từng cặp cạnh đối diện của hình vuông. Hình vuông có 4 trục đối xứng.
7. Hình chữ nhật, trục đối xứng là hai đường qua trung điểm từng cặp cạnh đối diện của hình chữ nhật. Hình chữ nhật có 2 trục đối xứng.
8. Đa giác đều có nhiều cạnh và có nhiều trục đối xứng.

Một số định lý liên quan đến đối xứng trục trong hình học

Định lý Colling

Các đường thẳng đối xứng qua ba cạnh của tam giác đồng quy khi và chỉ khi đi qua trực tâm của tam giác. Trong trường hợp này, điểm đồng quy nằm trên đường tròn ngoại tiếp tam giác.

Định lý Bliss

Cho ba đường thẳng song song đi qua ba trung điểm của ba cạnh của tam giác khi đó các đường thẳng đối xứng của ba cạnh tam giác đó qua ba đường thẳng này một cách lần lượt sẽ đồng quy tại đường tròn chín điểm của tam giác đó.

Định lý Paul Yiu

Cho đường thẳng qua tâm nội tiếp của tam giác và cắt ba cạnh BC, CA, AB của tam giác lần lượt tại X, Y, Z. Lấy các điểm X′, Y′, Z′ là đối xứng của X, Y, Z qua ba đường phân giác tương ứng. Khi đó ba điểm X′, Y′, Z′ thẳng hàng.

Chữ cái có tính chất đối xứng trục

A, B, C, D, E, H, I, M, O, K, U, V, W, X, Y

1. Hình học
2. Đường thẳng
3. Điểm
4. Tâm đối xứng
5. Định lý của Đào (hình côn)

Chú giải

Bản mẫuài viết về tính chất đối xứng qua Commons