1. Khái niệm về lũy thừa
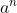
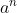
Trong đó:
Cơ số (a): Cơ số là số được nhân với chính nó. Trong phép tính lũy thừa a^n, cơ số a là số được nhân lên với chính nó n lần. Cơ số có thể là số nguyên, số thập phân, số âm, hoặc thậm chí là một biểu thức toán học phức tạp.
Ví dụ:
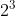
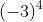
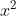
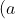
Cơ số xác định giá trị cơ bản của phép lũy thừa và có thể là bất kỳ giá trị số nào.
Số mũ (n): Số mũ chỉ số lần cơ số được nhân với chính nó, biểu thị số bước thực hiện phép lũy thừa. Số mũ phải là một số nguyên không âm (0, 1, 2, 3, ...).
Ví dụ:
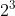
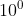
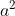
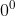
Ý nghĩa của các thành phần:
- Cơ số a xác định giá trị cơ bản của phép lũy thừa.
- Số mũ n chỉ số lần cơ số a được nhân với chính nó.
Khi kết hợp cơ số và số mũ, ta tạo ra một phép lũy thừa, giúp biểu diễn số lần một số được nhân với chính nó một cách rõ ràng. Lũy thừa không chỉ có giá trị trong toán học mà còn được áp dụng rộng rãi trong nhiều lĩnh vực như khoa học máy tính, kinh tế, vật lý, và nhiều lĩnh vực khác, để mô tả và tính toán các quy luật tỷ lệ, biến đổi.
2. Cách đọc lũy thừa
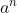
Ví dụ:
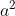
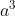
3. Các phép toán với lũy thừa
Nhân hai lũy thừa cùng cơ số
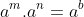
Khi nhân hai lũy thừa có cùng cơ số, cơ số được giữ nguyên và số mũ được cộng lại với nhau.
Chia hai lũy thừa có cùng cơ số
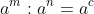
Khi chia hai lũy thừa có cùng cơ số (khác 0), cơ số vẫn giữ nguyên và số mũ được trừ đi.
Lũy thừa của lũy thừa
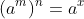
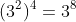
Nhân hai lũy thừa có cùng số mũ nhưng khác cơ số
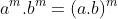
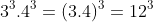
4. Bài tập ứng dụng
Câu 1: Viết biểu thức sau dưới dạng lũy thừa: 6 × 6 × 6 × 6 × 6
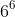
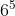
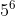
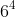
Giải đáp
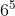
Chọn đáp án B.
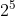
A. 2 là cơ số
B. 5 là số mũ
C. 2 là số mũ
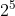
Giải thích
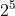
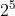
Chọn đáp án C.
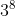
A. ba lũy thừa tám
B. ba mũ tám
C. lũy thừa bậc tám của số ba
D. tám lũy thừa ba
Giải thích
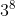
Chọn đáp án D.
Câu 4: Biểu diễn số 81 dưới dạng lũy thừa. Chọn câu không đúng.
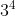
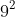
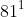
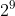
Giải thích
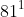
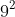
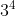
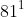
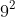
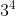
Vì vậy, đáp án A, B, C là đúng, còn D là sai.
Chọn đáp án D.
Câu 5: Chuyển đổi tích của 10 . 10 . 10 . 100 thành dạng lũy thừa với cơ số 10 sẽ ra kết quả nào?
A. 10^4
B. 10^5
C. 10^6
D. 10^7
Giải thích
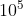
Chọn đáp án B.
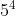
A. 20
B. 25
C. 125
D. 625
Giải thích
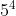
Chọn đáp án D.
5. Các ứng dụng thực tiễn của lũy thừa
- Các ứng dụng trong lĩnh vực tài chính:
Bài toán lãi suất khi gửi tiền vào ngân hàng: Trong tài chính, lũy thừa giúp tính lợi nhuận từ lãi suất kép (compound interest). Ví dụ, nếu bạn gửi một khoản tiền vào ngân hàng với lãi suất hàng năm, lợi nhuận tích lũy sau nhiều năm được tính bằng công thức A = P(1 + r)^t, trong đó A là số tiền cuối cùng, P là số tiền gửi ban đầu, r là lãi suất hàng năm (dưới dạng thập phân), và t là số năm gửi tiền.
Bài toán vay - mua trả góp: Trong các hợp đồng vay tiền hoặc mua trả góp, lũy thừa giúp tính tổng số tiền phải thanh toán sau một thời gian dài.
- Các ứng dụng trong đời sống và xã hội:
Bài toán tăng trưởng dân số: Trong lĩnh vực nhân khẩu học và kế hoạch hóa gia đình, lũy thừa giúp dự đoán sự gia tăng dân số trong một khu vực theo thời gian.
Bài toán về dữ liệu và thống kê: Trong các lĩnh vực liên quan đến dữ liệu và thống kê, lũy thừa thường được dùng để biểu thị và tính toán các tỷ lệ thay đổi, tỷ lệ tăng trưởng, hoặc mức độ biến động của dữ liệu.
- Các ứng dụng trong khoa học kỹ thuật:
Bài toán phóng xạ: Trong vật lý hạt nhân, lũy thừa được sử dụng để mô tả quá trình giảm dần của phóng xạ từ các vật chất.
Tính toán các cơn dư chấn sau động đất: Trong địa chất và xây dựng, lũy thừa được sử dụng để đánh giá cường độ động đất và tác động của nó lên các công trình. Các phương trình địa chấn áp dụng lũy thừa để mô tả mức độ dao động và ảnh hưởng.
Cường độ âm thanh và mức đo lường: Trong âm học và kỹ thuật, lũy thừa giúp mô tả mức độ âm thanh (được đo bằng đơn vị dB - decibel).
Các ứng dụng này chỉ là một phần trong số nhiều ứng dụng của lũy thừa trong thực tế. Từ những vấn đề phức tạp trong khoa học đến các quyết định tài chính hàng ngày, lũy thừa thể hiện vai trò quan trọng trong nền kinh tế và xã hội hiện đại.
Những ví dụ cụ thể cho thấy sức mạnh của lũy thừa không chỉ trong các bài toán lý thuyết mà còn trong các tình huống thực tiễn hàng ngày.
Lũy thừa với số mũ tự nhiên giúp chúng ta thực hiện các phép toán lặp lại hiệu quả. Từ tính toán lãi suất đầu tư, dự đoán tăng trưởng dân số, đến các ứng dụng trong khoa học và kỹ thuật như phóng xạ và cường độ âm thanh, lũy thừa đã và đang chứng tỏ tầm quan trọng của mình.
Hiểu và áp dụng lũy thừa không chỉ giúp giải quyết các bài toán phức tạp mà còn xây dựng nền tảng vững chắc cho các kỹ năng toán học cơ bản. Nó cũng mở rộng tầm nhìn và cách suy nghĩ logic trong các mô hình toán học và thực tế, góp phần vào sự phát triển trí tuệ của trẻ.
