Toán lớp 4 trang 112: Phân số bằng nhau với hướng dẫn chi tiết

1. Hướng dẫn giải bài tập toán lớp 4 trang 112 về phân số bằng nhau

Bài 1: Điền số thích hợp vào ô trống

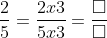
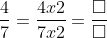
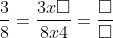
Cách giải:

Sử dụng quy tắc cơ bản về phân số

- Khi nhân cả tử và mẫu của một phân số với cùng một số nguyên dương khác 0, ta được một phân số tương đương với phân số ban đầu.

- Khi chia cả tử và mẫu của một phân số cho cùng một số nguyên dương khác 0, ta cũng được một phân số tương đương với phân số ban đầu.

Kết quả:

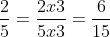
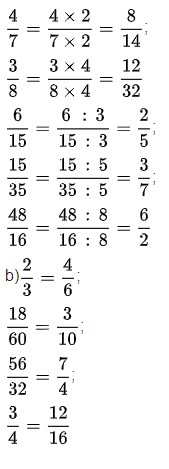
Bài 2: Thực hiện các phép tính và so sánh các kết quả

a) Tính 18 chia cho 3 và (18 nhân 4) chia (3 nhân 4)

b) Tính 81 chia cho 9 và (81 chia 3) chia (9 chia 3)

Nhận xét: Việc nhân (hoặc chia) cả số bị chia và số chia với cùng một số tự nhiên khác 0 sẽ không làm thay đổi giá trị của thương.

Phương pháp giải:

Khi có dấu ngoặc trong biểu thức, trước tiên phải tính toán phần trong ngoặc, sau đó mới xử lý phần bên ngoài.

Kết quả là:

a) 18 chia 3 bằng 6

(18 nhân 4) chia (3 nhân 4) = 72 chia 12 = 6

Do đó, kết quả của phép chia 18 : 3 và phép tính (18 x 4) : (3 x 4) đều là 6.

b) 81 chia 9 bằng 9

(81 chia 3) chia (9 chia 3) = 27 chia 3 = 9

Vì vậy, kết quả của phép chia 81 : 9 và phép tính (81 : 3) : (9 : 3) là giống nhau.

Bài 3: Điền số phù hợp vào chỗ trống

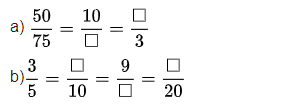
Cách giải:

Áp dụng các tính chất cơ bản của phân số:

- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số nguyên dương khác 0, phân số mới sẽ bằng phân số ban đầu.

- Nếu chia cả tử số và mẫu số của một phân số cho cùng một số nguyên dương khác 0, phân số mới vẫn giữ nguyên giá trị như phân số gốc.

Kết quả:

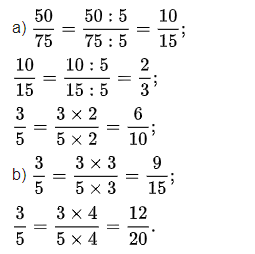
Kết quả được trình bày như sau:

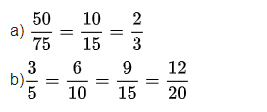
2. Lý thuyết Toán lớp 4 bài 112: Phân số tương đương

a) Có hai dải giấy có kích thước giống nhau.

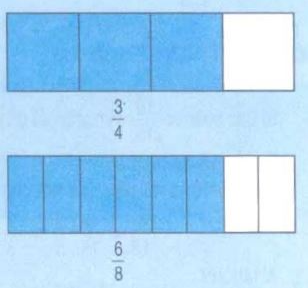
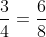
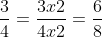
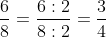
Dựa trên nhận xét này, ta có thể phát biểu tính chất cơ bản của phân số như sau:

• Nếu nhân cả tử số và mẫu số của một phân số với cùng một số nguyên dương khác 0, phân số mới sẽ bằng phân số gốc.

• Nếu tử số và mẫu số của một phân số đều chia hết cho cùng một số nguyên dương khác 0, thì sau khi chia, phân số mới sẽ bằng phân số gốc.

3. Các dạng bài tập về phân số lớp 4

Dạng 1: Tìm phân số của một số cho trước

1. Cách giải

Để tìm phân số a/b của số c, ta nhân số c với phân số a/b.

2. Ví dụ cụ thể

Ví dụ 1: Tính toán:

a. 4/15 của 30kg

b. 21/17 của 17m2

Giải đáp:

a. 4/15 của 30kg bằng 30 × 4/15 = 8 (kg).

b. 21/17 của 17m2 bằng 17 × 21/17 = 21 (m2)

Ví dụ 2: Một sân trường có chiều dài 120m, và chiều rộng là 5/6 của chiều dài. Tính diện tích sân trường.

Giải pháp:

Chiều rộng của sân trường hình chữ nhật là:

120 × 5/6 = 100 (m)

Diện tích của sân trường hình chữ nhật là:

120 × 100 = 12.000 (m2)

Kết quả: 12.000 m2

Dạng 2: Tìm số khi biết giá trị của phân số

1. Cách giải

Để tìm một số khi biết giá trị của phân số, ta chia số đó cho phân số đã cho.

2. Ví dụ cụ thể

Ví dụ 1: Tìm một số, biết rằng:

a. 5/7 của số đó bằng 25

b. 4/9 của số đó bằng 16

Giải pháp:

a. Số cần tìm là: 25 ÷ 5/7 = 35

b. Số cần tìm là: 16 ÷ 4/9 = 36

Ví dụ 2: Một xí nghiệp đã hoàn thành 5/9 kế hoạch và còn phải thực hiện thêm 560 sản phẩm nữa để hoàn tất kế hoạch. Tính tổng số sản phẩm theo kế hoạch của xí nghiệp.

Giải đáp:

Phần sản phẩm còn lại mà xí nghiệp cần hoàn thành là:

1 – 5/9 = 4/9 (theo kế hoạch)

Số sản phẩm xí nghiệp phải thực hiện theo kế hoạch là:

560 : 4/9 = 1260 (sản phẩm)

Kết quả là 1260 sản phẩm

4. Bài tập ứng dụng các dạng toán về phân số lớp 4

Bài 1: An có phân số 5/6 và viết 5 phân số tương đương với mẫu số lần lượt là 12, 30, 42, 66, 96. Bạn hãy cho biết những phân số An đã viết là gì?

Bài 2: Hồng cho rằng hai phân số 48/92 và 36/69 là bằng nhau, trong khi Lan lại khẳng định chúng không bằng nhau. Bạn hãy cho biết ai đúng?

Bài 3: Dũng cho rằng phân số 5/7 lớn hơn phân số 6/8, còn Bình thì nói phân số 6/8 lớn hơn phân số 5/7. Bạn hãy cho biết ai nói đúng?

Bài 4: Minh đã viết các phân số 2/3, 5/6, 7/9, 10/8, 1/2 và yêu cầu Hùng sắp xếp chúng từ bé đến lớn. Hùng đang gặp khó khăn trong việc sắp xếp. Hãy giúp Hùng làm điều đó.

Bài 5: Lan nói rằng cô ấy có thể tìm được 5 phân số lớn hơn 3/7 và nhỏ hơn 4/7. Bạn hãy cho biết, Lan có thể làm được điều này không?

Bài 6: Hãy tìm các phân số có mẫu số bằng 9 sao cho mỗi phân số đó lớn hơn 6/18 và nhỏ hơn 16/27.

Bài 7: Viết số 15 dưới dạng phân số với mẫu số lần lượt là 3, 5, 10.

Bài 8: Quan sát biểu thức 7/8 + 8/9 + 3/5, An cho rằng tổng của chúng nhỏ hơn 3. Bạn hãy kiểm tra xem nhận định của An có chính xác không?

Bài 9: Cho phân số a/b với a/b < 1. Nếu cộng cả tử số và mẫu số với cùng một số, ta sẽ có một phân số mới.

Bài 10: Với phân số 7/19, hãy tìm số tự nhiên cần thêm vào tử số và bớt khỏi mẫu số để có được phân số mới, sau khi rút gọn bằng phân số 19/15.

Bài 11: Tính toán:

Bài 12: Một sân trường có chiều dài 120m và chiều rộng bằng 5/6 chiều dài. Tính diện tích của sân trường.

Bài 13: Một cửa hàng có 4 tấn gạo và đã bán được 3/8 số gạo đó. Hãy tính số ki-lô-gam gạo còn lại trong cửa hàng.

Bài 14: Mẹ năm nay 49 tuổi và tuổi của con là 2/7 tuổi của mẹ. Bạn hãy tính tuổi của con năm nay.

Bài 15: Tìm một số biết rằng:

a) 2/7 của số đó bằng 42.

b) 9/34 của số đó bằng 108.

Bài 16: Một cửa hàng có 4 tấn gạo và đã bán được 3/8 số gạo. Tính số ki-lô-gam gạo còn lại trong cửa hàng.

Bài 17: Năm nay mẹ 49 tuổi, và tuổi của con là 3/7 tuổi của mẹ. Vậy năm nay con bao nhiêu tuổi?

Bài 18: Một lớp học gồm 40 học sinh, trong đó có 1/2 số học sinh được xếp loại giỏi, 3/4 số học sinh còn lại được xếp loại khá, phần còn lại là học sinh trung bình. Tính số học sinh trung bình trong lớp.

Bài 19: Một mảnh đất hình chữ nhật có chiều dài 50m và chiều rộng 36m. Diện tích của 5/9 phần đất được sử dụng để trồng vườn, phần còn lại được dùng làm ao. Tính diện tích phần đất làm ao.

Bài 20: Một trường học có tổng cộng 1200 học sinh. Trong đó, số học sinh có học lực trung bình chiếm 3/8 tổng số học sinh, số học sinh khá chiếm 2/5 số học sinh, phần còn lại là học sinh giỏi. Tính số học sinh giỏi của trường.

Bài 21: Có hai kho chứa tổng cộng 360 tấn cà phê. Nếu lấy 1/3 số cà phê ở kho thứ nhất và 2/5 số cà phê ở kho thứ hai thì số cà phê còn lại ở cả hai kho là như nhau. Tính số cà phê còn lại ở mỗi kho.

a) Tính số lượng cà phê ban đầu ở mỗi kho.

b) Xác định số tấn cà phê đã được lấy ra từ mỗi kho.

Bài 22: Một đội công nhân phải hoàn thành việc sửa chữa một đoạn đường qua ba giai đoạn. Trong giai đoạn đầu, đội sửa được 1/3 đoạn đường. Giai đoạn hai, đội sửa 3/7 đoạn đường còn lại. Để hoàn thành công việc, đội cần phải sửa thêm 160m nữa ở giai đoạn ba. Tính tổng chiều dài đoạn đường theo kế hoạch.

Bài 23: Có hai thùng dầu. Biết rằng 2/3 số dầu trong thùng đầu tiên là 24 lít và 3/4 số dầu trong thùng thứ hai là 36 lít. Tính tổng số lít dầu trong cả hai thùng.

Bài 24: Khối lớp 4 của một trường tiểu học có ba lớp: 4A, 4B và 4C. Biết rằng 2/3 số học sinh của lớp 4A là 18 học sinh; 3/4 số học sinh của lớp 4B là 24 học sinh; và 4/7 số học sinh của lớp 4C là 16 học sinh. Tính tổng số học sinh của khối lớp 4.

Bài 25: Nếu giảm 10m chiều dài của một tấm vải thì phần còn lại là 7/12 chiều dài ban đầu. Tính chiều dài tổng cộng của tấm vải.