1. Hướng dẫn giải bài tập toán lớp 4 trang 126: Phép cộng phân số
Bài 1:
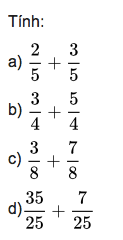
Phương pháp giải: Để thực hiện phép cộng hai phân số có cùng mẫu số, ta chỉ cần cộng các tử số với nhau và giữ nguyên mẫu số.
Đáp án:
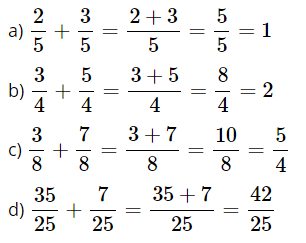
Bài 2: Hoàn thành câu bằng cách điền vào chỗ trống:
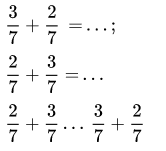
Phương pháp giải: Đầu tiên, tính giá trị của hai phân số, sau đó so sánh kết quả của chúng.
Đáp án:
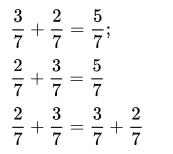
Bài 3: Hai xe tải cùng vận chuyển gạo từ kho. Xe tải đầu tiên đã chuyển 2/7 số gạo, còn xe tải thứ hai chuyển 3/7 số gạo. Tính tổng phần gạo cả hai xe đã chuyển.
Phương pháp giải: Tổng số gạo mà cả hai xe tải chuyển được là tổng của số gạo mỗi xe đã chuyển.
Đáp án:
Tổng số gạo mà hai ô tô đã chuyển là:
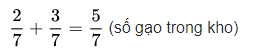
Kết quả: 5/7 số gạo trong kho.
2. Kiến thức về phép cộng phân số lớp 4
- Cộng hai phân số có cùng mẫu số
Nguyên tắc: Để thực hiện phép cộng hai phân số với cùng mẫu số, ta chỉ cần cộng các tử số lại với nhau và giữ nguyên mẫu số.
Ví dụ:
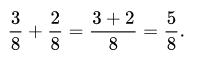
- Cộng hai phân số có mẫu số khác nhau
Nguyên tắc: Để cộng hai phân số có mẫu số khác nhau, trước tiên ta phải quy đồng mẫu số của chúng, sau đó thực hiện cộng như cộng hai phân số có cùng mẫu số.
Ví dụ:
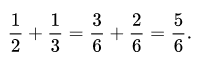
Lưu ý: Khi thực hiện phép cộng phân số, nếu kết quả không phải là phân số tối giản, hãy rút gọn nó về dạng phân số tối giản.
- Tính chất của phép cộng phân số:
+ Tính chất giao hoán: Đổi chỗ các phân số trong một tổng không làm thay đổi tổng đó: a + b = b + a
+ Tính chất kết hợp: Cộng tổng hai phân số với phân số thứ ba có thể thực hiện bằng cách cộng phân số thứ nhất với tổng của hai phân số còn lại: (a + b) + c = a + (b + c)
+ Cộng với số 0: Bất kỳ phân số nào cộng với 0 đều bằng chính phân số đó: a + 0 = 0 + a = a
- Các loại bài tập về phép cộng phân số:
+ Dạng 1: Tính tổng của hai phân số. Áp dụng quy tắc cộng cho phân số cùng mẫu hoặc khác mẫu để giải.
+ Dạng 2: Tính giá trị biểu thức. Áp dụng quy tắc ưu tiên thực hiện các phép toán nhân, chia trước, phép cộng trừ sau, và thực hiện các phép toán trong ngoặc trước.
+ Dạng 3: So sánh. Tính giá trị các biểu thức, sau đó sử dụng quy tắc so sánh các phân số để đưa ra kết luận.
+ Dạng 4: Tìm x. Xác định vai trò của (x) trong biểu thức và áp dụng các quy tắc đã học ở lớp 3 để tìm giá trị của (x).
+ Dạng 5: Tính nhanh. Sử dụng các tính chất của phép cộng phân số và nhóm các phân số để thực hiện tính toán một cách dễ dàng.
+ Dạng 6: Giải toán có lời văn.
- Cách học toán lớp 4 hiệu quả:
+ Phụ huynh nên khơi dậy tình yêu môn toán cho con bằng cách giải thích sự quan trọng của việc học toán, lồng ghép môn toán vào các câu đố vui và câu chuyện hàng ngày. Khi toán trở thành phần quen thuộc trong cuộc sống, các bé sẽ dễ tiếp cận và dần yêu thích môn toán hơn.
+ Đặt mục tiêu trong học tập rất quan trọng. Các em nên xác định mục tiêu rõ ràng cho môn toán ngay từ khi còn nhỏ và hướng tới mục tiêu lâu dài cho các môn học sau này. Đặt mục tiêu cao như đạt 9 điểm môn toán sẽ thúc đẩy các em nỗ lực nhiều hơn, khác với việc đặt mục tiêu chỉ đạt 7 điểm. Mục tiêu là động lực giúp các em biết mình cần học gì và vì sao học.
+ Phương pháp học tập là yếu tố cần thiết cho mọi môn học, đặc biệt là toán. Áp dụng phương pháp học đúng giúp các em biết cần học gì và thời điểm nào là hiệu quả nhất. Phương pháp học toán phù hợp sẽ giúp các em tập trung vào trọng tâm và đạt hiệu quả tốt hơn. Hãy tìm cho mình phương pháp học toán phù hợp với khả năng để đạt thành công.
+ Toán học thường được chia thành các chuyên đề và dạng bài tương ứng. Khi học đến một chuyên đề nào đó, các em nên ôn tập và nắm vững kiến thức trước khi chuyển sang chuyên đề khác. Để học toán hiệu quả, các em cần học đến đâu chắc đến đó và không nên nhảy từ kiến thức này sang kiến thức khác. Tuân thủ nguyên tắc học đến đâu luyện đến đó sẽ giúp nắm chắc kiến thức.
+ Lý thuyết toán học ở các cấp học ngày càng phức tạp, từ cơ bản đến nâng cao. Ở các lớp thấp hơn, kiến thức có phần dễ tiếp thu hơn, nhưng khi lên lớp cao, khó khăn sẽ tăng lên. Do đó, các em cần phải hệ thống hóa kiến thức và nắm vững lý thuyết. Lý thuyết là nền tảng để ứng dụng vào bài tập và cuộc sống sau này. Thiếu lý thuyết sẽ dẫn đến thiếu hụt kiến thức cơ bản, làm khó khăn trong việc giải bài tập.
+ Toán học yêu cầu các em phải luyện tập liên tục để đạt kết quả tốt. Nếu không chăm chỉ làm bài tập, lý thuyết sẽ trở thành kiến thức trừu tượng. Các em cần thực hành bài tập không chỉ ở lớp mà còn ở nhà, dành thời gian ôn tập và làm nhiều bài tập khó để củng cố và nâng cao kỹ năng. Thực hành thường xuyên sẽ giúp các em chủ động hơn trong học tập và khám phá kiến thức mới.
+ Đào sâu kiến thức giúp các em ghi nhớ lâu dài và ứng dụng đúng cách. Để hiểu sâu, các em cần ôn tập thường xuyên những gì đã học. Nếu không ôn lại, kiến thức sẽ dần bị quên theo thời gian. Đừng nghĩ rằng mình luôn nhớ như mới học, vì ôn tập nhiều sẽ giúp các em nhớ lâu và áp dụng kiến thức hiệu quả hơn.
3. Các bài tập toán nâng cao về phép cộng phân số
Bài 1: Tính toán:
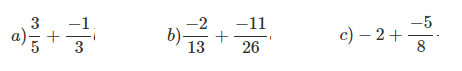
Đáp án: a) 4/15 b) -15/26 c) -21/8
Bài 2: Thực hiện phép tính
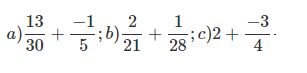
Đáp án: a) 7/30 b) 11/84 c) 5/4
Bài 3: Thực hiện phép tính
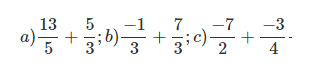
Đáp án: a) 64/15 b) 2 c) -17/4
Bài 4: Giải các tổng sau (trước tiên hãy rút gọn phân số)
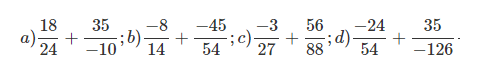
Đáp án: a) -11/4 b) -59/42 c) 52/99 d) -13/18
Bài 5: Tính tổng các phân số và rút gọn kết quả nếu có thể.
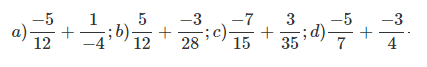
Đáp án: a) -2/3 b) 13/42 c) -8/21 d) -1/28
Bài 6: Điền dấu thích hợp ( > < = ) vào các khoảng trống.
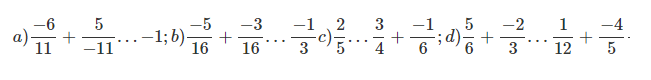
Đáp án:
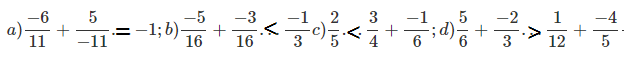
Bài 7: Điền các dấu thích hợp ( > < = ) vào các ô trống.
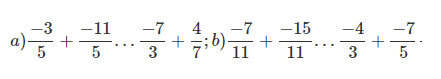
Đáp án:
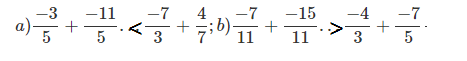
Bài 8: Xác định giá trị của x
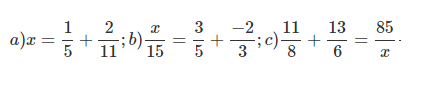
Đáp án: a) x = 21/55 b) x = -1 c) x = 24
Bài 9: Cho
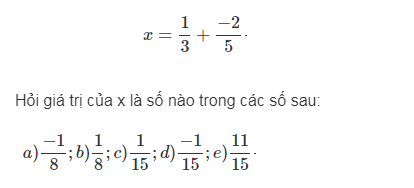
Đáp án: -1/15
Bài 10: So sánh các phân số dưới đây:
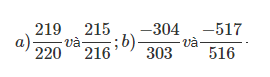
Đáp án: 219/220 lớn hơn 215/216
Bài 11: So sánh các phân số sau đây:
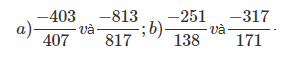
Đáp án: a) -4/407 nhỏ hơn -4/817
b) -251/138 nhỏ hơn -317/171
Bài 12: Biến phân số 3/4 thành tổng của hai phân số với tử số bằng 1.
Đáp án: 3/4 = (1+2)/4 = 1/4 + 2/4 = 1/4 + 1/2.
Bài 13: Biến phân số -7/12 thành tổng của hai phân số với tử số bằng -1.
Đáp án: -7/12 = (-3)+(-4)/12 = -3/12 = -4/12 = -1/4 + -1/3.
Bài 14: Chuyển các phân số dưới đây thành tổng của một số nguyên và một phân số.
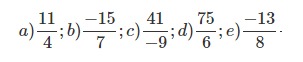
Đáp án:
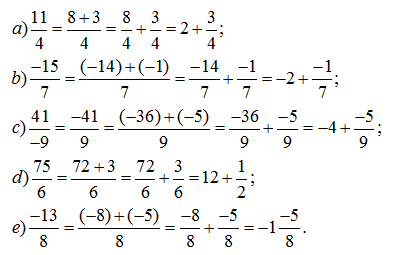
Bài 15: Chuyển các tổng sau đây thành phân số tương ứng:
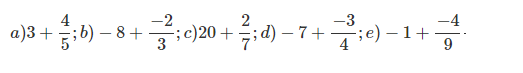
Đáp án: a) 19/5 b) -26/3 c) 142/7 d) -31/4 e) -13/9.
