Toán lớp 5: Bài tập trang 110

1. Những kiến thức cơ bản về bài toán tính diện tích

- Kiến thức lý thuyết về hình hộp chữ nhật:

+ Hình hộp chữ nhật là một khối gồm 6 mặt, tất cả đều là hình chữ nhật. Hai mặt đối diện nhau là mặt đáy của hình hộp, còn các mặt còn lại là các mặt bên.

+ Hình hộp chữ nhật có ba kích thước chính: chiều dài, chiều rộng và chiều cao.

+ Hình hộp chữ nhật có tổng cộng 8 đỉnh và 12 cạnh.

- Bài tập về tính diện tích xung quanh của hình hộp chữ nhật

+ Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích của 4 mặt bên của hình hộp.

+ Để tính diện tích xung quanh, ta nhân chu vi của mặt đáy với chiều cao (cùng đơn vị đo).

+ Công thức tính diện tích xung quanh hình hộp chữ nhật là: S = [2 x (a + b)] x h (trong đó S là diện tích xung quanh, a là chiều dài đáy, b là chiều rộng đáy, và h là chiều cao của hình hộp).

+ Để tính chiều cao, ta chia diện tích xung quanh cho chu vi của mặt đáy.

+ Để tính chu vi mặt đáy, ta chia diện tích xung quanh cho chiều cao.

- Bài tập về tính diện tích toàn phần của hình hộp chữ nhật

+ Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích của hai mặt đáy.

+ Công thức để tính diện tích toàn phần của hình hộp chữ nhật là: S = [2 x (a + b)] x h + 2 x a x b (S là diện tích toàn phần; a là chiều dài đáy; b là chiều rộng đáy; h là chiều cao).

(S đại diện cho diện tích toàn phần của hình hộp chữ nhật; a là chiều dài đáy; b là chiều rộng đáy; h là chiều cao của hình hộp chữ nhật)

2. Bài tập trang 110 về tính diện tích

Bài 1: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật với các kích thước sau:

a) Chiều dài 25 dm, chiều rộng 1,5 m và chiều cao 18 dm.

b) Kích thước: chiều dài từ 4 đến 5 m, chiều rộng từ 1 đến 3 m, và chiều cao 1,4 m.

Phương pháp giải:

- Để tính diện tích xung quanh của hình hộp chữ nhật, ta nhân chu vi của mặt đáy với chiều cao (cùng đơn vị đo).

- Để tính diện tích toàn phần của hình hộp chữ nhật, ta cộng diện tích xung quanh với diện tích của hai đáy.

Lời giải chi tiết:

a) Chuyển đổi 1,5m thành 15dm

Diện tích xung quanh của hình hộp chữ nhật là: (25 + 15) × 2 × 18 = 1440 (dm2)

Diện tích đáy của hình hộp chữ nhật là: 25 × 15 = 375 (dm2)

Diện tích toàn phần của hình hộp chữ nhật là: 1440 + 375 × 2 = 2190 (dm2)

b) Diện tích xung quanh hình hộp chữ nhật là: (4/5 + 1/3) × 2 × 1/4 = 17/30 (m2)

Diện tích đáy của hình hộp chữ nhật là: 4/5 × 1/3 = 4/15 (m2)

Diện tích toàn phần của hình hộp chữ nhật là: 17/30 + 4/15 × 2 = 11/10

Kết quả:

a) 1440 dm2; 2190 dm2;

b) 17/30 m2; 11/10 m2.

Bài 2: Một cái thùng hình chữ nhật không có nắp có chiều dài 1,5 m, chiều rộng 0,6 m và chiều cao 8 dm. Thùng được sơn bên ngoài. Tính diện tích sơn cần quét là bao nhiêu mét vuông?

Phương pháp giải:

Vì thùng không có nắp và chỉ quét mặt ngoài, diện tích cần sơn bằng diện tích xung quanh cộng với diện tích một mặt đáy.

Lưu ý: Các kích thước của thùng chưa đồng nhất đơn vị đo, nên cần quy đổi về cùng một đơn vị trước khi tính toán.

Lời giải chi tiết:

Tóm tắt nội dung

Thùng không có nắp, hình dạng hình hộp chữ nhật

Chiều dài: 1,5 m

Chiều rộng: 0,6 m

Chiều cao: 8 dm

Diện tích cần quét sơn bên ngoài là: ....?

Chuyển đổi: 8 dm = 0,8 m

Diện tích xung quanh thùng là: (1,5 + 0,6) × 2 × 0,8 = 3,36 (m2)

Diện tích mặt đáy thùng là: 1,5 × 0,6 = 0,9 (m2)

Tổng diện tích quét sơn là: 3,36 + 0,9 = 4,26 (m2)

Kết quả: 4,26 m2

Bài 3:

Đánh dấu Đ nếu đúng, S nếu sai.

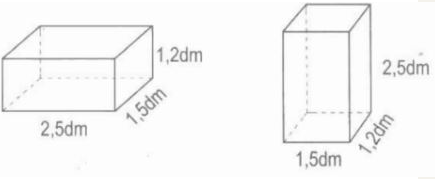
a) Diện tích toàn phần của hai hình hộp chữ nhật là như nhau.

b) Diện tích toàn phần của hai hình hộp chữ nhật không giống nhau.

c) Diện tích xung quanh của hai hình hộp chữ nhật là bằng nhau.

d) Diện tích xung quanh của hai hình hộp chữ nhật không giống nhau.

Phương pháp giải:

- Tính diện tích xung quanh và toàn phần của từng hình hộp rồi so sánh kết quả.

- Để tính diện tích xung quanh của hình hộp chữ nhật, ta nhân chu vi của mặt đáy với chiều cao (cùng đơn vị đo).

- Để tính diện tích toàn phần của hình hộp chữ nhật, ta cộng diện tích xung quanh với diện tích của hai mặt đáy.

Lời giải chi tiết:

+) Hình bên trái:

Diện tích xung quanh của hình hộp chữ nhật là: (2,5 + 1,5) × 2 × 1,2 = 9,6 (dm2)

Diện tích đáy của hình hộp chữ nhật là: 2,5 × 1,5 = 3,75 (dm2)

Diện tích toàn phần của hình hộp chữ nhật là: 9,6 + 3,75 × 2 = 17,1 (dm2)

+) Hình bên phải

Diện tích xung quanh của hình hộp chữ nhật là: (1,5 + 1,2) × 2 × 2,5 = 13,5 (dm2)

Diện tích đáy của hình hộp chữ nhật là: 1,5 × 1,2 = 1,8 (dm2)

Diện tích toàn phần của hình hộp chữ nhật là: 13,5 + 1,8 × 2 = 17,1 (dm2)

Ta có: 9,6 dm2 < 13,5 dm2, vì vậy diện tích xung quanh của hai hình hộp chữ nhật không giống nhau.

17,1 dm2 = 17,1 dm2, do đó diện tích toàn phần của hai hình hộp chữ nhật là bằng nhau.

Vậy kết quả là:

a) Đ

b) S

c) S

d) Đ

Chú ý:

Hai hình hộp chữ nhật được so sánh có một hình nằm ngang và một hình đứng, nhưng cả hai đều có ba kích thước là 2,5 dm, 1,5 dm, và 1,2 dm. Do đó, mặc dù diện tích toàn phần giống nhau, diện tích xung quanh lại khác nhau.

3. Những lưu ý khi giải bài tập về diện tích xung quanh và toàn phần của hình hộp chữ nhật

Để giải tốt các bài tập về diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật, học sinh cần chú ý một số điểm sau:

- Trước khi bắt đầu, hãy đồng nhất các số đo chiều dài, chiều rộng và chiều cao về cùng một đơn vị. Việc bỏ qua bước này có thể dẫn đến kết quả sai lệch so với đáp án. Để tránh mất điểm không đáng có, học sinh cần đọc kỹ đề bài và nếu các số đo chưa đồng nhất về đơn vị, cần chuyển đổi chúng về một đơn vị chung.

- Để giải bài tập về diện tích xung quanh và diện tích toàn phần hình hộp chữ nhật hiệu quả, học sinh cần ôn luyện và nắm vững các công thức liên quan, đồng thời học cách áp dụng linh hoạt phù hợp với dữ liệu bài toán. Điều này đòi hỏi học sinh phải suy luận từ dữ liệu đề bài và các công thức đã học, cùng với việc luyện tập nhiều bài toán để hiểu sâu về vấn đề.

- Khi làm bài tập, học sinh nên thực hiện từng bước một cách chắc chắn. Sau khi thành thạo các bước cơ bản và rèn luyện các kỹ năng liên quan, có thể thử sức với các bài tập nâng cao để củng cố kiến thức.

- Để thành công trong việc giải bài tập tính diện tích xung quanh và diện tích toàn phần của hình chữ nhật, cũng như các bài toán khác, học sinh cần phát triển tính kiên trì. Kỹ năng suy luận và tư duy logic là rất quan trọng, nhưng nỗ lực và kiên trì là yếu tố không thể thiếu. Khi gặp bài toán khó, đừng vội bỏ cuộc; hãy đọc kỹ đề bài, phân tích cẩn thận dữ liệu và liên kết chúng với kiến thức và công thức đã học để tìm ra phương án giải quyết phù hợp.

Trên đây là các nội dung liên quan đến bài tập Toán lớp 5 ở trang 110. Để tìm hiểu chi tiết về các dạng bài toán này, các bạn có thể tham khảo bài viết: Hình hộp chữ nhật là gì? Công thức tính diện tích xung quanh và thể tích của hình hộp chữ nhật?. Chúc các bạn học tốt!