1. Toán lớp 5 trang 88: Tính diện tích hình tam giác
Bài 1: Tính diện tích của hình tam giác với đáy dài a và chiều cao h:
a) a = 30,5 dm và h = 12 dm
b) a = 16 dm và h = 5,3 m.
Hướng dẫn giải
Sử dụng công thức tính diện tích: S = (a x h) / 2, trong đó S là diện tích, a là độ dài đáy và h là chiều cao.
Chú ý: Đảm bảo a và h có cùng đơn vị đo lường.
Câu trả lời:
a) Diện tích của hình tam giác là:
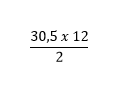
b) Chuyển đổi 5,3 m = 53 dm.
Tính diện tích của hình tam giác là:
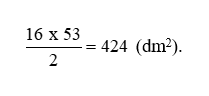
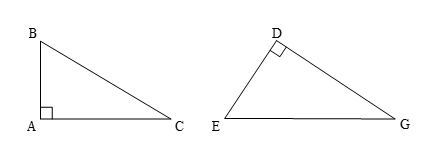
Bài 2: Xác định đáy và chiều cao tương ứng cho từng hình tam giác vuông dưới đây:
Phương pháp giải bài toán
Nhìn vào hình minh họa và áp dụng kiến thức về đáy và chiều cao của tam giác.
Hướng dẫn giải bài tập:
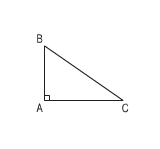
Hình tam giác vuông ABC:
- Đáy là AC và chiều cao tương ứng là BA.
- Đáy là AB và chiều cao tương ứng là CA.
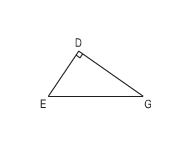
Hình tam giác vuông DEG:
- Đáy là DE và chiều cao tương ứng là GD.
- Đáy là DG và chiều cao tương ứng là ED.
Bài 3:
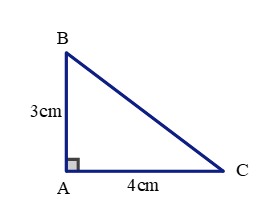
a) Tính diện tích của hình tam giác vuông ABC.
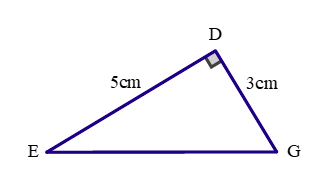
b) Tính diện tích của hình tam giác vuông DEG.
Diện tích của hình tam giác vuông được tính bằng cách nhân độ dài của hai cạnh góc vuông rồi chia cho 2.
Lời giải:
a, Diện tích của tam giác vuông ABC là:
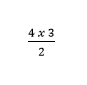
b, Diện tích của tam giác vuông DEG là:
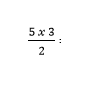
Ghi nhớ: Để tính diện tích của tam giác vuông, nhân độ dài hai cạnh góc vuông rồi chia cho 2 (phải cùng đơn vị đo).
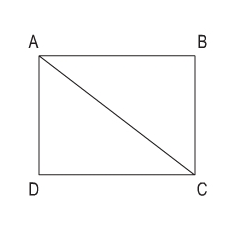
Giải Toán lớp 5 trang 89 Bài 4: a) Đo các cạnh của hình chữ nhật ABCD và tính diện tích của tam giác ABC.
b) Đo chiều dài các cạnh của hình chữ nhật MNPQ cùng với độ dài cạnh ME
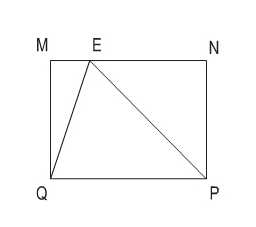
Tính toán:
- Tổng diện tích của hai tam giác MQE và NEP.
- Tính diện tích của hình tam giác EPQ.
Phương pháp giải
- Diện tích của tam giác vuông ABC được tính bằng cách nhân độ dài hai cạnh góc vuông (cùng đơn vị đo) rồi chia cho 2.
- Diện tích của tam giác EQP = Diện tích hình chữ nhật MNPQ trừ đi tổng diện tích của hai tam giác MQE và NEP.
Lời giải:
a, Sau khi đo, ta có: AB = 4cm, BC = 3cm
Tính diện tích của hình tam giác ABC:
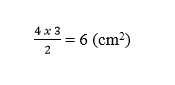
b, Sau khi đo, ta có: MQ = NP = 3cm, MN = PQ = 4cm, ME = 1cm
Do đó, NE = 4 - 1 = 3 cm
Tính diện tích của hình chữ nhật MNPQ:
4 x 3 = 12 (cm²)
Diện tích của tam giác MQE là:
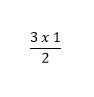
Diện tích của tam giác NEP là:
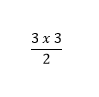
Tổng diện tích của hai tam giác là:
1,5 + 4,5 = 6 (cm²)
Diện tích của tam giác EQP là:
12 - 6 = 6 (cm²)
Lưu ý: Tổng diện tích hai tam giác MQE và NEP bằng diện tích tam giác EPQ, vì nó bằng nửa diện tích của hình chữ nhật MNPQ. Do đó, tổng diện tích của hai tam giác và diện tích tam giác EPQ có thể tính như sau:
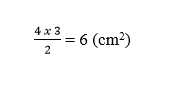
2. Cách giải bài tập về diện tích hình tam giác
I* Các công thức cần nhớ
Xét tam giác với các cạnh BC = a, AC = b, AB = c, có:
• ha, hb, hc
là chiều dài của đường cao tương ứng với các cạnh BC, CA, AB
• R là bán kính của đường tròn ngoại tiếp tam giác;
• r là bán kính của đường tròn nội tiếp tam giác;
• p = (a + b + c) / 2 là nửa chu vi của tam giác;
• S là diện tích của tam giác.
Dưới đây là các công thức tính diện tích của tam giác ABC:
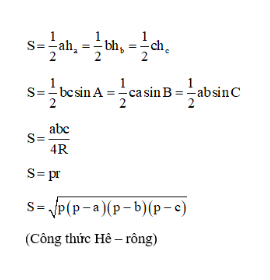
+ Phương pháp giải: Sử dụng linh hoạt các công thức đã học dựa trên thông tin bài toán.
Ví dụ minh họa
Bài 1. Cho tam giác ABC với AB = 3, AC = 6, và ∠BAC = 60°. Tính diện tích của tam giác ABC.
Lời giải:
Diện tích của tam giác ABC được tính như sau:
S = 1/2 × AB × AC × sin(BAC)
= 1/2 × 3 × 6 × sin 60° = 9√3/2 = 9√3/2 (đvdt).
Bài 2. Tam giác ABC với AC = 4, ∠BAC = 30°, và ∠ACB = 75°. Tính diện tích của tam giác ABC.
Lời giải:
Theo định lý về tổng ba góc trong tam giác ABC, ta có:

Bài 3. Tam giác ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC được tính như sau:
Lời giải:
Nửa chu vi của tam giác ABC là:
p = (a + b + c) / 2 = (21 + 17 + 10) / 2 = 24 (đvđd)
Theo công thức Hê-rông, diện tích tam giác ABC được tính như sau:
S = √[p(p - a)(p - b)(p - c)]
= √[24 × (24 - 21) × (24 - 17) × (24 - 10)] = √84 = 84 (đvdt).
Bài 4. Tam giác đều nội tiếp đường tròn với bán kính R = 4 cm có diện tích là bao nhiêu?
Lời giải:
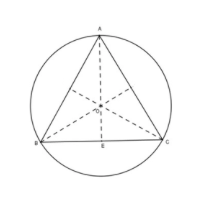
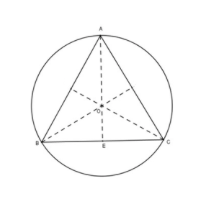
Giả sử tam giác đều ABC có cạnh a (cm, a > 0) thỏa mãn yêu cầu của bài toán.
Theo đề bài, đường tròn có bán kính R = 4 cm là đường tròn ngoại tiếp tam giác ABC. Tâm O của đường tròn chính là giao điểm của ba đường trung trực của tam giác.
Vì tam giác ABC đều nên O cũng chính là trực tâm của tam giác.
Đặt E là trung điểm của cạnh BC
Theo đó, ta có: AE = 2/3 AO (dựa trên tính chất của trọng tâm)
Vì AO = R = 4 cm
Nên AE = 6 cm
Vì tam giác ABC đều nên trung tuyến AE đồng thời là đường cao.
Áp dụng định lý Pythagoras trong tam giác vuông ABE, ta có:
AB² = AE² + BE²
Từ đó, ta suy ra: a² = 6² + (a/2)² ⇒ a = 4√3 (cm)
Do đó, diện tích của tam giác đều ABC là:
S = AB × AC × BC / 4R = (4√3)³ / 4 × 4 = 12√3 = 433 / 4 × 4 = 123 (cm²).
3. Các bài tập tương tự
Bài 1: Trong Δ ABC, nếu đường cao AH = 2/3 BC thì diện tích của tam giác là bao nhiêu?
A. 2/5 BC² B. 2/3 BC²
C. 1/3 BC² D. 1/3 BC
Giải pháp:
Diện tích của tam giác được tính bằng: S = 1/2 × cạnh đáy × đường cao.
Trong đó: cạnh đáy là b và đường cao là h.
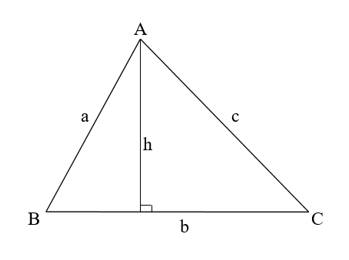
Vậy, diện tích tam giác là: S = 1/2 × AH × BC = 1/2 × 2/3 BC × BC = 1/3 BC².
Chọn đáp án C.
Bài 2: Tam giác ABC có đáy BC = 6 cm và đường cao AH = 4 cm. Tính diện tích của tam giác ABC.
A. 24 cm² B. 12 cm²
C. 24 cm D. 14 cm²
Giải:
Diện tích của tam giác ABC là S = 1/2 x AH x BC = 1/2 x 6 x 4 = 12 cm².
Chọn đáp án B.
Bài 3: Tam giác ABC vuông tại A với đáy BC = 5 cm và AB = 4 cm. Tính diện tích của tam giác.
A. 12 cm² B. 10 cm²
C. 6 cm² D. 3 cm²
Lời giải:
Áp dụng định lý Pytago, ta có: AB² + AC² = BC² nên AC = √ (BC² - AB²)
⇒ AC = √ (5² - 4²) = 3 cm.
Vậy diện tích tam giác ABC là: S = 1/2 x AB x AC = 1/2 x 4 x 3 = 6 cm².
Chọn đáp án C.
Bài 4: Cho tam giác ABC với đường cao AH. Biết AB = 15 cm, AC = 41 cm, HB = 12 cm. Tính diện tích của tam giác ABC.
A. 234 cm² B. 214 cm²
C. 200 cm² D. 154 cm²
Lời giải:
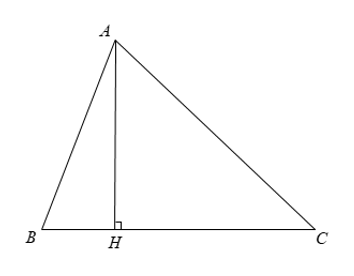
Áp dụng định lý Pythagoras, ta có:
+ Xét tam giác ABH, ta có AH² + BH² = AB² ⇒ AH = √ (AB² - BH²)
⇒ AH = √ (15² - 12²) = 9 cm.
+ Xét tam giác ACH, ta có AC² = AH² + HC² ⇒ HC = √ (AC² - AH²)
⇒ HC = √ (41² - 9²) = 40 cm.
Vì vậy, diện tích tam giác ABC là: S = 1/2 AH.BC = 1/2 AH (HB + HC) = 1/2 × 9 × (12 + 40) = 234 cm².
Chọn đáp án A.
Bài 5: Cho tam giác ABC với AB = 6 cm, AC = 8 cm. Hai đường cao từ B và C lần lượt là BH và CK. Biết BH = 9 cm. Tính CK.
A. 12 cm B. 15 cm
C. 9 cm D. 8 cm
Giải quyết:
Diện tích của tam giác ABC là:
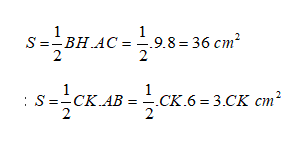
Từ đó, ta có: 3CK = 36, suy ra CK = 12 cm.
Chọn đáp án A.
Bài 6: Trong tam giác vuông ABC tại điểm A với AB = 6 cm và AC = 8 cm, tìm chiều dài của đường cao từ A?
A. 4 cm B. 4,5 cm
C. 4,8 cm D. 5 cm
Giải pháp:
Áp dụng định lý Pytago cho tam giác ABC, ta có:
Tính BC2: AB2 + AC2 = 62 + 82 = 100
Do đó: BC = 10 cm
Diện tích của tam giác ABC được tính như sau:
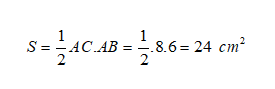
Đặt AH là đường cao từ đỉnh A trong tam giác ABC.
Như vậy:
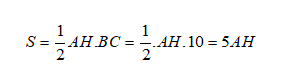
Từ đó: 5AH = 24 nên AH = 4,8 cm
Chọn đáp án C
Bài 7: Trong tam giác ABC, với đường cao AH = 6 cm và diện tích tam giác ABC là 30 cm2. Gọi M là trung điểm của BC. Tính diện tích tam giác ABM.
A. 10 cm2 B. 12 cm2
C. 20 cm2 D. 15 cm2
Giải chi tiết:

Chọn đáp án D
Bài 8: Trong tam giác ABC có diện tích 40 cm2. M là trung điểm của AC. Tìm diện tích tam giác ABM?
A. 10 cm2 B. 20 cm2
C. 25 cm2 D. Không đủ thông tin
Giải đáp:

Chọn đáp án B
Bài 9: Trong tam giác ABC với AB = 4 cm và AC = 7 cm, BH và CK lần lượt là các đường vuông góc từ đỉnh B và C. Tính tỷ số BH/CK?
A. 4/7 B. 7/4
C. 4/3 D. Đáp án khác
Giải đáp:

Chọn đáp án A
Bài 10: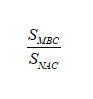
A. 1/2 B. 2
C. 1 D. Không thể xác định
Giải đáp:

Chọn đáp án C
Mytour hy vọng mang đến cho quý khách hàng những thông tin tư vấn hữu ích. Xem thêm nội dung liên quan tại: Nội dung vở bài tập Toán lớp 5 bài 87 Luyện tập Diện tích hình tam giác. Cảm ơn quý khách đã hợp tác!
