1. Tìm hiểu về hình thang
1.1 Định nghĩa hình thang
Hình thang là một tứ giác lồi với hai cạnh đối song song. Hai cạnh song song này được gọi là đáy của hình thang, trong khi hai cạnh còn lại gọi là các cạnh bên.
Các loại hình thang đặc biệt
- Hình thang vuông: Đây là hình thang có một góc vuông, còn được gọi là hình thang vuông.
- Hình thang cân: Đây là hình thang có hai góc kề trên một cạnh đáy bằng nhau, được gọi là hình thang cân.
- Hình thang vuông cân: Đây là hình thang vừa vuông vừa cân, đồng thời cũng được gọi là hình chữ nhật.
1.2 Ứng dụng của hình thang
Hình thang có nhiều ứng dụng trong thực tế, chẳng hạn như:
- Hình thang thường được áp dụng trong thiết kế kiến trúc như xây dựng nhà ở, cầu đường, để tạo nên sự cân đối và hài hòa cho công trình.
- Hình thang còn được dùng để tính diện tích, chu vi, và thể tích của các vật thể có hình dáng giống hoặc gần giống như hình thang, chẳng hạn như mái nhà, bể chứa nước, hộp quà, v.v.
- Hình thang được sử dụng trong việc biểu diễn dữ liệu thống kê qua các loại biểu đồ hình thang như biểu đồ tần suất hay biểu đồ phân phối tần suất, giúp minh họa phân bố và xu hướng.
- Hình thang còn là công cụ hữu ích trong việc giải thích các khái niệm toán học như tỷ lệ, phân số, và phương trình bậc nhất.
1.3 Cách nhận diện hình thang
– Có 5 đặc điểm để nhận diện hình thang như sau:
+ Tứ giác có hai cạnh đối song song
+ Hình thang có một góc vuông gọi là hình thang vuông
+ Hình thang có hai góc kề một đáy giống nhau được gọi là hình thang cân
+ Hình thang có hai cạnh bên bằng nhau được gọi là hình thang cân
+ Hình thang có hai đường chéo bằng nhau cũng là hình thang cân
– Các dấu hiệu nhận diện hình thang cân:
+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
+ Hình thang với hai đường chéo bằng nhau là hình thang cân.
+ Hình thang có hai trục đối xứng trùng nhau với hai đáy gọi là hình thang cân
+ Nếu hai cạnh bên của hình thang bằng nhau thì đó là hình thang cân
+ Hình thang có thể nội tiếp đường tròn được gọi là hình thang cân
2. Các đặc điểm và tính chất của hình thang
a. Tính chất liên quan đến góc
- Tổng của hai góc kề một cạnh bên trong hình thang bằng 180 độ, với các góc nằm ở cùng một phía của hai cạnh đáy song song
- Trong hình thang cân, hai góc kề cùng một đáy có giá trị bằng nhau
b. Tính chất liên quan đến cạnh
- Nếu hai cạnh đáy của hình thang bằng nhau, thì hai cạnh bên sẽ cũng bằng nhau và song song với nhau
- Khi hai cạnh bên của hình thang song song thì chúng bằng nhau, và các cạnh đáy cũng bằng nhau
c. Tính chất của đường trung bình
Đường trung bình là đoạn thẳng nối hai điểm giữa của hai cạnh bên trong hình thang
- Đường thẳng nối điểm giữa một cạnh bên của hình thang và song song với hai cạnh đáy sẽ đi qua điểm giữa của cạnh bên còn lại
- Đường trung bình của hình thang vừa song song với hai cạnh đáy vừa bằng một nửa tổng chiều dài của hai đáy
Hình thang có bốn đỉnh, cho phép nối bất kỳ hai đỉnh khác nhau để tạo thành đường chéo. Do đó, hình thang có tổng cộng bốn đường chéo, nhưng thực tế chỉ có hai đường chéo phân biệt vì chúng trùng nhau.
3. Công thức để tính diện tích hình thang
Để tính diện tích hình thang, chúng ta sử dụng công thức: trung bình cộng của hai cạnh đáy nhân với chiều cao giữa hai đáy.
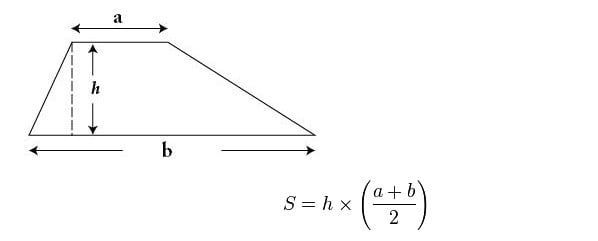
Trong đó:
+ S: diện tích của hình thang.
+ h: chiều cao từ đỉnh đến đáy của hình thang.
+ a và b: các cạnh đáy của hình thang.
Theo công thức trên, diện tích hình thang được xác định bằng chiều cao nhân với trung bình cộng của hai đáy. Có một câu thơ dễ nhớ về công thức tính diện tích hình thang như sau:
Để tính diện tích hình thang
Cộng hai đáy lớn và nhỏ vào với nhau
Cộng lại và nhân với chiều cao
Chia đôi để lấy nửa là ra kết quả
Phương pháp tính diện tích hình thang cân
Bên cạnh việc sử dụng công thức tính diện tích hình thang thông thường, bạn cũng có thể chia hình thang cân thành các phần nhỏ để tính diện tích từng phần rồi cộng lại.
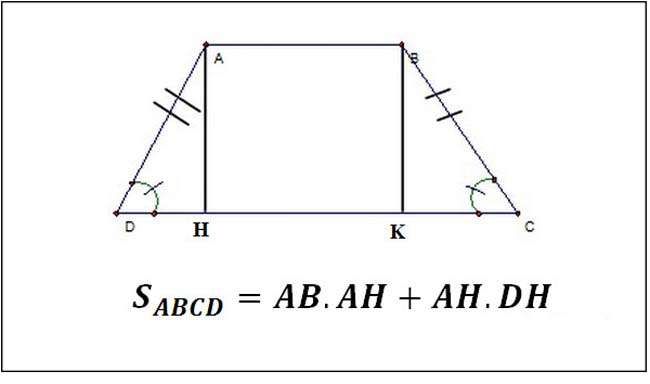
Giả sử hình thang cân ABCD với hai cạnh bên AD và BC bằng nhau. Khi đó, đường cao AH và BK chia hình thang thành một hình chữ nhật ABHK và hai hình tam giác ADH và BCK. Tính diện tích hình chữ nhật ABHK và hai hình tam giác ADH, BCK, sau đó cộng tất cả diện tích để có diện tích của hình thang ABCD.
Công thức tính diện tích hình thang với 4 cạnh (bài toán nâng cao):
Khi bài toán cung cấp độ dài của 4 cạnh, với cạnh đáy a, c (c lớn hơn a), và hai cạnh bên b và d, bạn có thể tính diện tích hình thang theo công thức dưới đây.
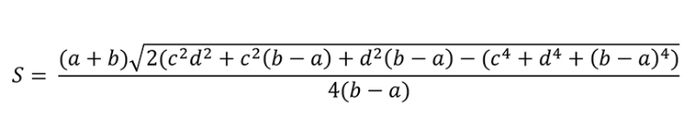
Trong đó:
S: Diện tích hình thang.
a: Cạnh đáy nhỏ hơn.
c: Cạnh đáy lớn hơn.
b, d: Các cạnh bên của hình thang.
4. Toán lớp 5 trang 93, 94 Diện tích hình thang có đáp án chi tiết
Bài 1: Tính diện tích của hình thang với hai cạnh đáy lần lượt là a và b, và chiều cao h:
a) a = 14cm; b = 6cm; h = 7cm
b) a = 2/3 m; b = 1/2 m; h = 9/4 m
c) a = 2,8m; b = 1,8m; h = 0,5m
Phương pháp giải
Sử dụng công thức tính diện tích hình thang:
S = (a + b) x h / 2
Trong đó S là diện tích; a và b là các cạnh đáy; h là chiều cao.
Gợi ý đáp án:
a) Tính diện tích của hình thang như sau:
(14 + 6) x 7 / 2 = 70 (cm²)
b) Diện tích của hình thang tính được là:
(2/3 + 1/2) x 9/4 / 2 = 21/16 = 1,3125 (m²)
c) Diện tích của hình thang tính được là:
(2,8 + 1,8) x 0,5 / 2 = 23/20 = 1,15 (m²)
Bài 2: Một thửa ruộng hình thang có đáy lớn dài 120 m. Đáy nhỏ bằng 2/3 đáy lớn và dài hơn chiều cao 5 m. Với tỷ lệ thu hoạch 64,5 kg thóc cho mỗi 100 mét vuông, tính tổng số thóc thu hoạch được trên thửa ruộng này.
Phương pháp giải
- Xác định độ dài đáy nhỏ bằng cách nhân đáy lớn với 2/3.
- Tính chiều cao bằng cách trừ 5 m từ độ dài đáy nhỏ.
- Tính diện tích ruộng bằng cách lấy tổng chiều dài hai đáy nhân với chiều cao rồi chia cho 2.
- Tính tỷ lệ giữa diện tích ruộng và 100 m².
- Tính lượng thóc thu hoạch: nếu diện tích ruộng gấp bao nhiêu lần 100 m² thì lượng thóc cũng sẽ gấp bấy nhiêu lần 64,5 kg.
Gợi ý đáp án:
Đáy nhỏ của thửa ruộng hình thang là:
120 × 2/3 = 80 (m)
Chiều cao của thửa ruộng hình thang là:
80 – 5 = 75 (m)
Diện tích thửa ruộng là:
(120 + 80) x 75 / 2 = 7500 (m²)
Mỗi mét vuông thu hoạch được số thóc là:
64,5 chia 100 = 0,645 (kg thóc)
Tổng số thóc thu hoạch trên thửa ruộng là:
0,645 × 7500 = 4837,5 (kg)
Kết quả: 4837,5 kg
Bài 3: Đúng thì ghi Đ, sai thì ghi S:
a) Các hình thang AMCD, MNCD, NBCD đều có diện tích bằng nhau.
b) Diện tích hình thang AMCD bằng 1/3 diện tích của hình chữ nhật ABCD.
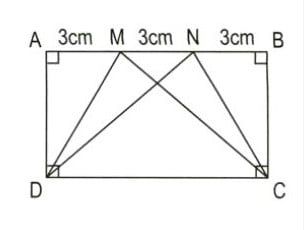
Phương pháp giải
Sử dụng công thức tính diện tích hình thang:
S = (a + b) x h / 2
Trong đó, S là diện tích; a, b là chiều dài của hai đáy; h là chiều cao của hình thang.
Gợi ý đáp án:
a) Do ba hình thang AMCD, MNCD, NBCD có cùng đáy lớn, đáy nhỏ và chiều cao, nên diện tích của chúng là bằng nhau.
⟶ Đánh dấu Đ vào ô trống.
b) Diện tích của hình chữ nhật ABCD được tính bằng:
(3 + 3 + 3) x AD = 9 x AD
Diện tích của hình thang AMCD tính như sau:
(3 + 9) x AD / 2 = 6 x AD
Kết quả là:
(6 x AD) / (9 x AD) = 6/9 = 2/3
Do đó, diện tích của hình thang AMCD bằng với diện tích của hình chữ nhật ABCD.
