1. Tam giác đều
Bài tập 1: Trong các hình sau (H.4.1), hình nào là tam giác đều?
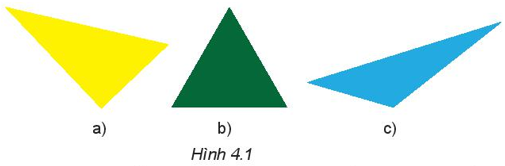
Trả lời: Trong số các hình (H.4.1), hình b) chính là tam giác đều.
Tìm kiếm các ví dụ thực tế về hình tam giác đều.
Trả lời:
Một số ví dụ thực tế về hình tam giác đều bao gồm mặt của trò chơi Rubik hình tam giác và kệ sách có thiết kế dạng tam giác đều.
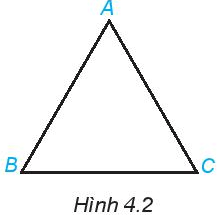
Bài tập 2: Xem hình 4.2 về tam giác đều ABC. Xác định các đỉnh, cạnh, và góc của tam giác ABC. Dùng thước thẳng để đo và so sánh các cạnh của tam giác ABC. Dùng thước đo góc để đo và so sánh các góc của tam giác ABC.
Trả lời:
Trong hình 4.2, tam giác đều ABC có: a) Các đỉnh: A, B, C b) Các cạnh: AB, BC, AC c) Các góc: Góc A, Góc B, Góc C
Sử dụng thước thẳng, ta thấy rằng: AB = BC = AC, tức là các cạnh của tam giác đều này bằng nhau.
Sử dụng thước đo góc, chúng ta nhận thấy rằng các góc A, B, và C đều có độ lớn bằng 60 độ, cho thấy các góc của tam giác đều ABC cũng bằng nhau và đều là 60 độ.
Bài 3: Thực hành trang 78 Toán lớp 6 Tập 1: Vẽ tam giác đều ABC với cạnh dài 3 cm theo hướng dẫn.
Bước 1: Vẽ đoạn thẳng AB có chiều dài 3 cm.
Bước 2: Dùng ê ke với góc 60 độ để tạo góc BAx bằng 60 độ.
Bước 3: Vẽ tiếp góc ABy cũng bằng 60 độ. Khi hai đường BAx và By giao nhau tại điểm C, ta có tam giác đều ABC.
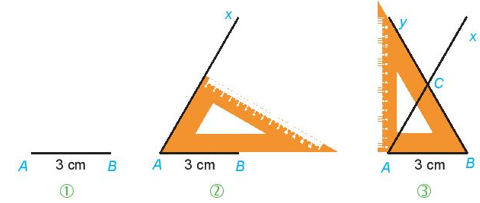
Kiểm tra hình vẽ: Các cạnh của tam giác ABC có đồng đều không? Các góc có giống nhau không?
Trả lời:
a) Sau khi hoàn tất vẽ, kiểm tra lại hình sẽ thấy:
b) Các cạnh AB, AC và BC đều dài 3 cm, nghĩa là các cạnh của tam giác ABC đều bằng nhau.
c) Các góc A, B và C đều bằng 60 độ, tức là các góc trong tam giác ABC đều bằng nhau và đều có giá trị 60 độ.
Bài 4. Hướng dẫn cách vẽ tam giác đều với mỗi cạnh dài 2 cm.
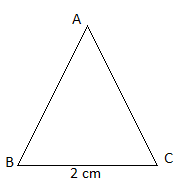
Các bước để vẽ tam giác đều ABC với mỗi cạnh dài 2 cm như sau:
a) Bước 1: Vẽ đoạn thẳng AB dài 2 cm.
b) Bước 2: Dùng ê ke có góc 60 độ để tạo góc BAx bằng 60 độ.
c) Bước 3: Vẽ góc ABy sao cho góc này là 60 độ. Khi đường thẳng BAx và By giao nhau tại điểm C, ta sẽ có tam giác đều ABC.
Bài 5. Phát biểu nào dưới đây là không chính xác?
A. Nếu tam giác MNP có MN = NP, thì tam giác MNP là tam giác đều.
B. Nếu các góc của tam giác MNP đều bằng 60 độ, thì tam giác MNP là tam giác đều.
C. Nếu tam giác MNP có MN = NP = PQ, thì tam giác MNP là tam giác đều.
D. Nếu tam giác MNP có NP = PQ, điều này không đảm bảo rằng tam giác MNP là tam giác đều.
Đáp án chính xác là: A
2. Hình vuông
Bài 1: Hoạt động 3, trang 79, Toán lớp 6, Tập 1
Tìm kiếm một số ví dụ về hình vuông trong cuộc sống hàng ngày.
Trả lời: Một số ví dụ về hình vuông trong thực tế bao gồm mặt của xúc xắc, đĩa và gạch lát sàn.
Bài 2: Hoạt động 4, trang 79, Toán lớp 6, Tập 1
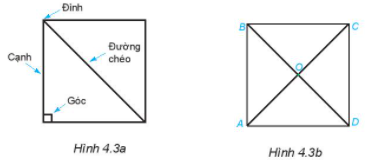
Xem xét Hình 4.3a. Xác định các đỉnh, cạnh và đường chéo của hình vuông ABCD (H.4.3b). Dùng thước thẳng để đo và so sánh độ dài các cạnh cũng như các đường chéo của hình vuông. Sử dụng thước đo góc để đo và so sánh các góc của hình vuông.
Trả lời:
Hình vuông ABCD có các đặc điểm sau: Đỉnh: A, B, C, D; Cạnh: AB, BC, CD, DA; Đường chéo: AC, BD
Sau khi đo bằng thước thẳng, chúng ta thấy rằng: AB = BC = CD = DA, cho thấy tất cả các cạnh của hình vuông đều có độ dài bằng nhau. Đường chéo AC = BD, chứng tỏ hai đường chéo của hình vuông có độ dài bằng nhau. Đo góc cho thấy các góc A, B, C, D đều bằng 90 độ, tức là các góc của hình vuông đều bằng nhau và đều là 90 độ.
Bài 3: Thực hành 1, trang 79, Toán lớp 6, Tập 1
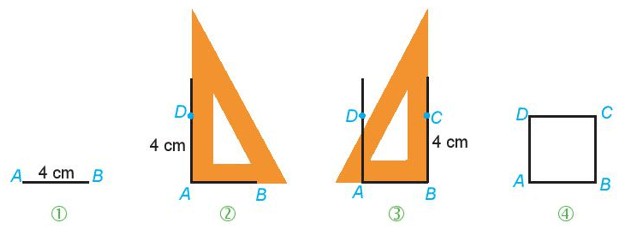
Vẽ hình vuông ABCD với cạnh dài 4 cm theo các bước hướng dẫn.
Bước 1: Vẽ đoạn thẳng AB dài 4 cm.
Bước 2: Vẽ một đường thẳng vuông góc với AB tại điểm A. Xác định điểm D trên đường thẳng này sao cho AD có độ dài 4 cm.
Bước 3: Tiếp theo, vẽ một đường thẳng vuông góc với AB tại điểm B. Xác định điểm C trên đường thẳng này sao cho BC dài 4 cm.
Bước 4: Kết nối điểm C và D để hoàn thành hình vuông ABCD. Kiểm tra lại hình vừa vẽ: Các cạnh có bằng nhau không? Các góc có đồng đều không?
Trả lời:
Khi hoàn thành việc vẽ, kiểm tra hình vẽ: Ta thấy rằng các cạnh AB, BC, CD, AD đều bằng nhau, chứng tỏ hình vuông có các cạnh đều. Đồng thời, các góc A, B, C, D đều bằng 90 độ, xác nhận rằng các góc của hình vuông là đồng đều và bằng 90 độ.
Gấp và cắt một hình vuông từ một tờ giấy hình chữ nhật như trong hình minh họa. Chuẩn bị giấy, kéo và thực hiện theo hướng dẫn. Cắt hình vuông theo hai đường chéo để có hai hình vuông nhỏ.
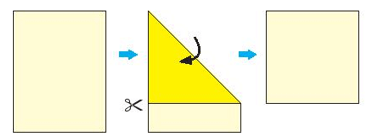
Cắt hình vuông theo hai đường chéo để phân chia thành bốn tam giác. Sau đó, ghép lại để tạo thành hai hình vuông.
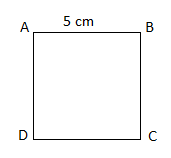
Bài 4: Hướng dẫn cách vẽ hình vuông với cạnh dài 5 cm.
Hướng dẫn chi tiết:
a) Bước 1: Vẽ đoạn thẳng CD dài 5 cm.
b) Bước 2: Tại điểm D, vẽ một đường thẳng vuông góc với CD. Xác định điểm A trên đường thẳng này sao cho AD dài 5 cm.
c) Bước 3: Tại điểm C, vẽ một đường thẳng vuông góc với CD. Xác định điểm B trên đường thẳng này sao cho BC dài 5 cm. d) Bước 4: Nối điểm A với B để hoàn thiện hình vuông ABCD.
Bài 5. Một hình vuông có chu vi 16 cm. Bình phương độ dài của một đường chéo của hình vuông là:
A. 16 cm
B. 20 cm
C. 25 cm
D. 32 cm
Hướng dẫn giải:
Để tính độ dài một cạnh của hình vuông, ta có: 16 ÷ 4 = 4 (cm).
Bình phương độ dài của đường chéo hình vuông được tính bằng công thức: 42 + 42 = 32 (cm).
Lựa chọn chính xác là D.
3. Hình lục giác đều
Bài 1: Xem xét hình 4.5.
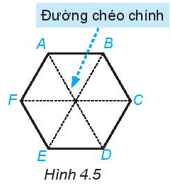
Liệt kê các đường chéo chính của hình lục giác đều ABCDEF.
Trả lời: Các đường chéo chính của hình lục giác đều ABCDEF là AD, BE, CF.
So sánh độ dài của các đường chéo chính.
Trả lời: Đo bằng thước thẳng, ta thấy rằng các đường chéo chính AD, BE và CF đều có cùng độ dài.
Bài 2: Luyện tập trang 80 Toán lớp 6 Tập 1 với hình lục giác đều như trong Hình 4.6.
Chúng ta biết rằng hình lục giác đều được tạo thành từ 6 tam giác đều. Liệt kê các tam giác đều đó và cho biết có thêm tam giác đều nào khác trong hình không?
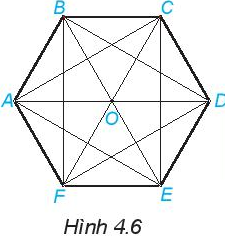
Trả lời:
a) Các tam giác đều tạo thành hình lục giác đều gồm: tam giác ABO, BCO, CDO, DEO, EFO, và FAO.
b) Ngoài các tam giác đều trên, hình còn chứa: tam giác ACE (vì AC = AE = CE) và tam giác BDF (vì BD = DF = BF).
Bài 3: Vận dụng trang 81 Toán lớp 6 Tập 1. Tìm các hình ảnh thực tế có dạng hình lục giác đều.
Trả lời: Một số hình ảnh thực tế có dạng hình lục giác đều bao gồm: gạch lát tường, khay đựng kẹo, đèn thả, mái đình, và nhiều ví dụ khác.
Bài 4: Để lắp đặt một trạm biến áp phục vụ cho sáu ngôi nhà, nên đặt trạm biến áp ở đâu để khoảng cách từ trạm đến sáu ngôi nhà là như nhau? Biết rằng sáu ngôi nhà nằm tại sáu đỉnh của hình lục giác đều.
Hướng dẫn giải: Để đảm bảo khoảng cách từ trạm biến áp đến sáu ngôi nhà là bằng nhau, bạn nên đặt trạm biến áp ở trung tâm của hình lục giác đều mà sáu ngôi nhà tạo thành. Trung tâm của hình lục giác đều sẽ có khoảng cách đều đến tất cả các đỉnh của nó. Vì vậy, việc đặt trạm biến áp tại điểm O trung tâm của hình lục giác đều sẽ đảm bảo khoảng cách đều từ trạm đến mỗi ngôi nhà.
Bài 5: Hình lục giác đều được cấu thành từ:
A. 3 tam giác đều.
B. 4 tam giác đều.
C. 5 tam giác đều.
D. 6 hình tam giác đều
Đáp án chính xác là D.
