Tổng hợp các công thức tính đạo hàm nhanh cho học sinh lớp 11

Các công thức tính đạo hàm nhanh sẽ giúp bạn nắm bắt kiến thức toán học quan trọng một cách dễ dàng. Bài viết này từ Mytour cung cấp các công thức tính nhanh đạo hàm u+v, giúp bạn giải bài tập hiệu quả hơn. Hãy khám phá để tự tin hơn trong việc học tập.

Các định nghĩa và quy tắc cơ bản

Các định nghĩa và quy tắc cơ bản trong việc áp dụng công thức tính đạo hàm nhanh là nền tảng quan trọng để bạn hiểu rõ cách vận dụng kiến thức vào thực tế. Dưới đây là các thông tin cần thiết để bạn có thể làm bài tập hiệu quả.

Định nghĩa về đạo hàm

Đạo hàm là tỷ lệ thể hiện sự thay đổi giữa giá trị hàm số và biến số tại một điểm cụ thể. Nó cho thấy tốc độ thay đổi của hàm tại điểm đó, giúp xác định độ dốc của đồ thị hàm trong toán học.

Trong vật lý, đạo hàm thường dùng để mô tả vận tốc tức thời hoặc sự biến đổi của một đại lượng theo thời gian. Công thức tính đạo hàm đóng vai trò quan trọng trong việc nghiên cứu chuyển động, tối ưu hóa và phân tích đồ thị, được ứng dụng rộng rãi trong nhiều ngành khoa học và kỹ thuật.

Ý nghĩa của đạo hàm

Đạo hàm mang lại giá trị quan trọng không chỉ trong toán học mà còn trong các ứng dụng thực tiễn. Trong toán học, nó giúp xác định tốc độ thay đổi của hàm, tìm cực trị và nghiên cứu tính đơn điệu của hàm. Ngoài ra, đạo hàm được áp dụng trong vật lý để tính vận tốc, gia tốc, trong kinh tế để phân tích lợi nhuận biên và trong kỹ thuật để thiết kế hệ thống điều khiển. Về mặt hình học, đạo hàm biểu thị độ dốc của tiếp tuyến với đồ thị hàm số tại một điểm, phản ánh xu hướng thay đổi tại đó.

Các quy tắc cơ bản để áp dụng công thức đạo hàm lớp 11

Học sinh lớp 11 thường xuyên sử dụng các công thức và quy tắc tính đạo hàm nhanh để giải các bài toán. Những quy tắc này giúp đơn giản hóa quá trình tính toán, hỗ trợ giải quyết nhanh chóng các bài toán phức tạp. Sau đây là các quy tắc đạo hàm cơ bản:

• Quy tắc đạo hàm của tổng: (𝑢 + 𝑣)′ = 𝑢′ + 𝑣′
• Quy tắc đạo hàm của tích: (𝑢 * 𝑣)′ = 𝑢′ * 𝑣 + 𝑢 * 𝑣′
• Quy tắc đạo hàm của thương: (𝑢𝑣)’ = 𝑢′ * 𝑣 - 𝑢 * 𝑣′ / 𝑣²
• Quy tắc đạo hàm của hàm hợp: Nếu 𝑦 = 𝑓(𝑔(𝑥)), thì 𝑦′ = 𝑓′(𝑔(𝑥))⋅𝑔′(𝑥)

Tổng hợp các công thức đạo hàm cơ bản

Đạo hàm là một khái niệm thiết yếu trong giải tích, dùng để mô tả sự thay đổi của hàm số theo biến độc lập. Dưới đây là những công thức tính đạo hàm phổ biến mà Mytour đã biên soạn, giúp bạn học tập hiệu quả hơn.

Công thức tổng quát về đạo hàm

Đạo hàm là phép toán được dùng để xác định mức độ thay đổi của hàm số tại một điểm. Công thức tính đạo hàm tổng quát thường được tính thông qua giới hạn như sau:

𝑓’(𝑥) = (f(x) − f(x0)) / (x − x0)

Giải thích:

• Δ 𝑥 = 𝑥 − 𝑥0: biểu thị sự thay đổi của biến 𝑥.

• Δ 𝑦 = 𝑓(𝑥) − 𝑓(𝑥0): biểu thị sự thay đổi tương ứng của hàm số.

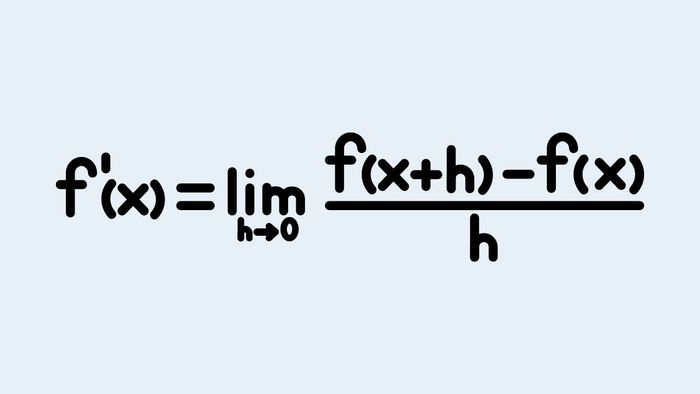
Laptop là công cụ hữu ích hỗ trợ bạn giải các bài toán đạo hàm hiệu quả hơn. Sử dụng phần mềm hỗ trợ, bạn sẽ tính đạo hàm nhanh chóng và chính xác hơn. Dưới đây là một số mẫu Laptop phổ biến:

Các công thức đạo hàm cơ bản

Ngoài công thức đạo hàm u+v, còn có nhiều công thức cơ bản khác. Những công thức này là nền tảng để bạn giải các bài toán đạo hàm phổ biến trong chương trình học. Dưới đây là các công thức cơ bản cần nhớ:

1. (c)'=0, với 𝑐 là một hằng số
2. (xn)'=nxn-1 với 𝑛 ∈ 𝑅
3. (x)' = 12x
4. (1x)' =-1x2
5. (nx)' = 1n * nxn-1, n ∈ N ,n>1 
6. (ex)'=ex
7. (ax)' =ax * ln a
8. (ln x)'=1x
9. (logax)' = 1x * ln a
10. (ax+bcx+d)'=ad - bx(cx+d)2
11. (ax2+bx+cex+f)'=aex2+2afx+(bf-ce)(ex+f)2

Công thức đạo hàm bậc cao

Đạo hàm bậc cao là một khái niệm quan trọng trong giải tích, giúp tính toán các đạo hàm nhiều lần của hàm số. Dưới đây là các công thức tính đạo hàm bậc cao phổ biến, giúp bạn tính toán nhanh chóng và chính xác:

1. (xm)(n)=m(m-1)...(m-n+1)xm-n khi m≥n
2. (xm)(n)=0 khi m
3. (logax)(n) = (-1)n-1 * (n-1)!ln a * 1/xn
4. (ln x)(n) = (-1)n-1 * (n-1)! * x^(-n)

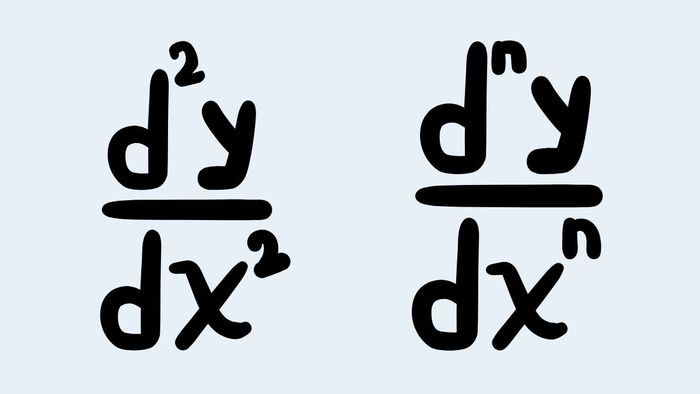
1. (ekx)(n)= kn * ekx
2. (ax)(n)= (ln a)^n * ax
3. (sin ax)(n) = an * sin(ax + n/2)
4. (cos ax)(n) = an * cos(ax + n/2)
5. (1/(ax + b))(n) = (-1)^n * an * n! * 1/(ax + b)^(n+1)

Các công thức đạo hàm của hàm số lượng giác

Đạo hàm của các hàm số lượng giác giúp ta nắm bắt sự biến thiên của các đại lượng theo các tham số. Sau đây là những công thức đạo hàm cơ bản của các hàm lượng giác:

1. (sin x)' = cos x
2. (cos x)' = -sin x
3. (tan x)' = 1/cos²x
4. (cot x)' = -1/sin²x
5. (sec x)' = sec x * tan x
6. (csc x)' = -csc x * cot x
7. (arcsin x)' = 1/√(1 - x²)
8. (arccos x)' = -1/√(1 - x²)
9. (arctan x)' = 1/(x² + 1)

Các công thức đạo hàm cập nhật mới nhất

Việc hiểu rõ các công thức đạo hàm không chỉ là chìa khóa giải các bài toán trong học tập mà còn là cơ sở cho nhiều ứng dụng trong đời sống. Sau đây là bảng tổng hợp các công thức đạo hàm từ cơ bản đến nâng cao:

Các dạng bài tập liên quan đến đạo hàm

Bài tập đạo hàm không chỉ giúp kiểm tra khả năng áp dụng lý thuyết mà còn rèn luyện kỹ năng giải quyết các bài toán phức tạp trong toán học. Dưới đây là một số dạng bài tập về đạo hàm giúp bạn củng cố và nâng cao kiến thức của mình.

Dạng 1: Bài tập đạo hàm theo khái niệm và định nghĩa của đạo hàm

Dạng bài tập này giúp bạn làm quen với việc tính đạo hàm. Để giải bài tập, bạn cần sử dụng định nghĩa đạo hàm để tính đạo hàm tại một điểm của hàm số. Ví dụ: Tính đạo hàm của hàm số y=f(x)=x²-x, áp dụng công thức đạo hàm theo định nghĩa.

Giải bài toán

Ta có: y = (x₀ + x)² - (x₀ + x) - (x₀² + x₀) = x(x + 2x₀ - 1)

Do đó, f'(x) = x₀y x = x₀(x + 2x₀ - 1)

=> f'(x) = 2x₀ - 1

Dạng 2: Xây dựng phương trình tiếp tuyến của hàm số tại điểm tiếp xúc

Phương trình tiếp tuyến của hàm số tại một điểm có thể biểu diễn dưới dạng y = f'(x₀)(x - x₀) + f(x₀), với f'(x₀) là đạo hàm tại điểm x₀ và f(x₀) là giá trị hàm tại x₀. Sau đó, áp dụng các công thức tính đạo hàm nhanh để giải quyết bài toán.

Ví dụ: Xây dựng phương trình tiếp tuyến của hàm số f(x) = x² tại điểm x₀ = 1

Giải bài toán

Ta có f'(x) = 2x₀

x₀ = 1 ⇒ f(1) = 1 ; f'(1) = 1

Vậy, phương trình tiếp tuyến là: y = f'(1)(x - 1) + f(1) = 2(x - 1) + 1 = 2x - 1

Dạng 3: Chứng minh đẳng thức với điều kiện liên quan đến đạo hàm cho trước

Ở dạng bài này, yêu cầu là chứng minh một đẳng thức liên quan đến đạo hàm, có thể là kiểm tra tính chính xác của một mối quan hệ giữa các đạo hàm hoặc xác định điều kiện để đẳng thức đúng. Bạn có thể sử dụng các công thức đạo hàm để giải quyết bài toán này.

Ví dụ: Cho y = f(x) = 2x + 6. Chứng minh y' < 10

Bài giải

Áp dụng công thức đạo hàm, ta có y' = 2 < 10

Do đó, y' < 10

Dạng 4: Giải phương trình và bất phương trình có liên quan đến đạo hàm

Ở dạng bài này, bạn sẽ áp dụng công thức đạo hàm để giải các phương trình hoặc bất phương trình. Mục tiêu là tìm giá trị của x sao cho đạo hàm của hàm số thỏa mãn các điều kiện đã cho.

Ví dụ: Giải bất phương trình f'(x) > 0 với f(x) = x^2 - 4x + 3

Bài giải

Ta có f'(x) = 2x - 4, giải bất phương trình f'(x) > 0.

=> 2x - 4 => x^2

Dạng 5: Cho hệ số góc, viết phương trình tiếp tuyến

Ở dạng bài này, bạn sẽ được cung cấp hệ số góc của tiếp tuyến tại một điểm cụ thể và phương trình hàm số. Dựa vào công thức tính đạo hàm, bạn có thể tìm được phương trình tiếp tuyến của hàm số tại điểm đã cho.

Ví dụ: Cho hàm số y = x^2 + 1. Viết phương trình tiếp tuyến tại điểm có hệ số góc m = 4.

Giải pháp

Ta có m = 4, y' = 2x => x = 2

Hoành độ x = 2 => y = 5

Phương trình tiếp tuyến có dạng: y = m(x - x0) + y0 => y = 4(x - 2) + 5

Phương trình tiếp tuyến với hệ số góc 4 là: y = 4x - 3

Dạng 6: Sử dụng đạo hàm và nguyên hàm để giải bài toán

Dạng bài này yêu cầu bạn áp dụng công thức đạo hàm và nguyên hàm để giải các bài toán. Bạn cần tính đạo hàm hoặc nguyên hàm của hàm số rồi sử dụng chúng để giải các phương trình liên quan.

Ví dụ: Cho hàm số f(x) = x³ + 2x² - 5x + 4. Tính đạo hàm và nguyên hàm của hàm số này.

Bài giải

• Đạo hàm của f(x) là: f'(x) = 3x² + 4x - 5
• Nguyên hàm của f(x) là: F(x) = x⁴ / 4 + 2x³ / 3 - 5x² / 2 + 4x + C

Dạng 7: Tính đạo hàm cấp cao

Dạng bài này yêu cầu bạn sử dụng công thức để tính đạo hàm cấp cao của một hàm số. Bạn cần tính đạo hàm nhiều lần cho đến khi đạt được cấp độ đạo hàm yêu cầu trong bài toán.

Ví dụ: Áp dụng công thức để tính đạo hàm cấp 2 của hàm số f(x) = 4x³ + 9x² - 10x + 6

Giải quyết bài toán

Đạo hàm bậc 1 của f(x): f'(x) = 12x² + 18x - 10

=> Đạo hàm bậc 2 của f(x): f''(x) = 24x + 18

Các câu hỏi phổ biến

Khi tìm hiểu đạo hàm, học sinh và sinh viên thường gặp phải một số vấn đề khó khăn trong việc hiểu và áp dụng các công thức. Dưới đây là các giải đáp cho những câu hỏi thường gặp liên quan đến đạo hàm.

Cách ghi nhớ bảng đạo hàm hiệu quả

Để nhớ bảng đạo hàm hiệu quả, bạn nên nhóm các công thức theo từng loại như hàm bậc, hàm lượng giác, hàm mũ,... và học từng nhóm một. Việc sử dụng bảng công thức trong các bài tập thực tế sẽ giúp bạn ghi nhớ nhanh hơn. Đặc biệt, việc ôn luyện thường xuyên và ứng dụng liên tục sẽ giúp bạn củng cố kiến thức lâu dài.

Phương pháp giải bài tập đạo hàm nhanh chóng

Giải bài tập đạo hàm nhanh yêu cầu bạn phải thuộc lòng các công thức cơ bản và nắm vững quy tắc đạo hàm như của tổng, tích, thương. Đọc kỹ đề bài để nhận diện dạng hàm số và áp dụng công thức phù hợp. Luyện tập đều đặn sẽ giúp bạn phản xạ nhanh và giải quyết bài toán chính xác hơn.

Việc làm chủ các công thức tính đạo hàm nhanh sẽ giúp bạn giải bài tập hiệu quả và tiết kiệm thời gian. Hy vọng với các công thức đạo hàm u+v trên từ Mytour, bạn sẽ tự tin hơn khi giải các bài toán đạo hàm. Khi đã thành thạo, bạn có thể áp dụng chúng vào bài tập và kỳ thi một cách dễ dàng.