
Các công thức tổ hợp, chỉnh hợp, hoán vị thường gây nhầm lẫn cho học sinh THPT khi phân biệt giữa các định nghĩa và công thức tính toán. Để làm bài tập và thi hiệu quả, học sinh cần phân biệt rõ ba loại công thức này. Bài viết sau sẽ giới thiệu chi tiết về công thức chỉnh hợp, tổ hợp, hoán vị để học sinh hiểu rõ hơn.
Hoán vị trong Toán học và các dạng thường gặp
Đầu tiên chúng ta sẽ tìm hiểu về hoán vị và các loại hoán vị phổ biến nhất:
Khái niệm của hoán vị
Để giải thích một cách đơn giản, từ “hoán” có nghĩa là “đổi chỗ” và từ “vị” có nghĩa là “vị trí”. Ví dụ, khi chúng ta có một tập hợp X gồm n phần tử khác nhau (với điều kiện n ≥ 0), thì mỗi cách sắp xếp các phần tử trong tập X theo một thứ tự nhất định được gọi là một hoán vị của n. Thông thường, số lượng hoán vị của n được ký hiệu là “Pn”.

Có bao nhiêu dạng hoán vị phổ biến?
Hiện nay có ba loại hoán vị thường gặp nhất là:
Hoán vị loại lặp
Đây là dạng hoán vị khi chúng ta có n đối tượng và trong đó có ni đối tượng thuộc loại i, mỗi loại có cấu trúc giống nhau. Nói một cách đơn giản, trong việc sắp xếp n đối tượng, có n1 đối tượng thuộc loại a1, n2 đối tượng thuộc loại a2,… và nk đối tượng thuộc loại ak (n1 + n2 + n3 +…..+ nk = n) được sắp xếp theo thứ tự ngẫu nhiên và được gọi là hoán vị loại lặp với cấp n và dạng (n1, n2,…, nk) thuộc k phần tử.
Mỗi kiểu sắp xếp của n đối tượng được coi là một hoán vị loại lặp với n.
Công thức tính toán cho loại hoán vị loại lặp như sau:
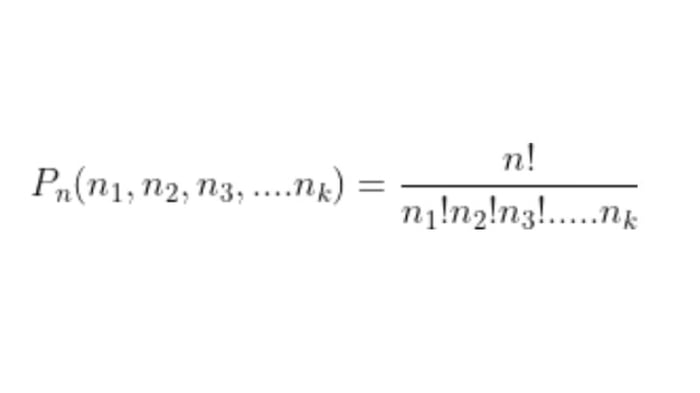
Trong đó, chúng ta có:
- “Pn” là hoán vị loại lặp với cấp “n” và dạng (n1, n2,…, nk) của “k” phần tử.
- n = n1 + n2 +…..+ nk: Số lượng phần tử.
- “n1” là số lượng phần tử “a1” có cấu trúc giống nhau.
- “n2” là số lượng phần tử “a2” có cấu trúc giống nhau.
- “nk” là số lượng phần tử “ak” có cấu trúc giống nhau.
Hoán vị loại vòng
Đây là dạng hoán vị trong đó các phần tử có thể sắp xếp thành một vòng với số lượng phần tử k lớn hơn 1 và “k” là một số nguyên. Công thức tính toán cho hoán vị loại vòng là:
Q(n) = (n-1)!
Hoán vị loại đồng nhất
Thường được gọi là hoán vị không đổi chỗ, đây là loại hoán vị mà mỗi phần tử được giữ nguyên vị trí của nó, không có sự hoán đổi giữa các phần tử.
Tổ hợp, chỉnh hợp là khái niệm gì?
Trước khi đi vào việc học các công thức về tổ hợp, chỉnh hợp, chúng ta cần hiểu rõ định nghĩa sau đây:
Khái niệm về tổ hợp
Tổ hợp là phương pháp chọn các phần tử từ một nhóm lớn mà không quan tâm đến thứ tự. Đôi khi chúng ta cũng có thể đếm số lượng tổ hợp có thể có. Tổ hợp chập “k” của “n” phần tử là số lượng nhóm có “k” phần tử được lấy từ tổng số “n” phần tử, mà không quan tâm đến thứ tự của các phần tử trong nhóm.
Với mỗi tập hợp con có “k” phần tử trong một tập hợp lớn gồm “n” phần tử (với n>0), tổ hợp chập “k” của “n” phần tử được xem là các nhóm có “k” phần tử được chọn từ tổng số “n” phần tử.
Khái niệm chỉnh hợp
Đây là phương pháp lựa chọn các phần tử từ một tập hợp lớn hơn và vẫn quan tâm đến thứ tự sắp xếp của chúng. Điều này khác với tổ hợp vì chỉnh hợp yêu cầu các phần tử được chọn phải có thứ tự cụ thể.

Chỉnh hợp chập “k” của “n” là một tập con của tập lớn S gồm “n” phần tử. Tập con này có chính xác “k” phần tử từ tập S và được sắp xếp theo một thứ tự nhất định.
Bộ công thức tổ hợp, chỉnh hợp, hoán vị đầy đủ kèm ví dụ
Dưới đây là bộ công thức tổ hợp, chỉnh hợp, hoán vị đầy đủ nhất trong Toán học:
Công thức tính toán chỉnh hợp
Theo khái niệm đã đề cập, số lượng chỉnh hợp chập “k” của một tập hợp có “n” phần tử (1≤ k ≤ n) được tính bằng công thức sau:
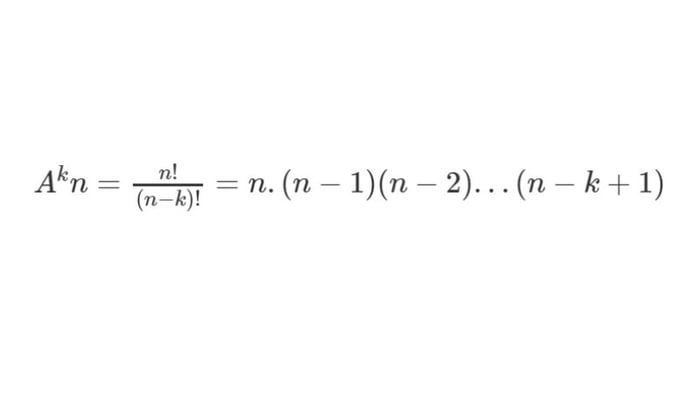
Ví dụ minh họa 1: Chúng ta có bao nhiêu cách để sắp xếp 3 bạn Hoàng, Hiếu, Hưng vào 2 chỗ ngồi có sẵn?
Đáp án:
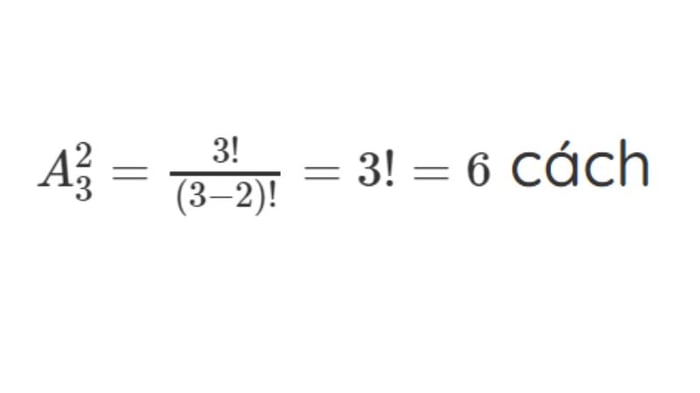
Ví dụ minh họa 2: Có bao nhiêu số có 04 chữ số khác nhau có thể được tạo ra từ các chữ số 1, 2, 3, 4, 5, 6, 7.
Đáp án:
Chúng ta có thể tạo ra các số gồm bốn chữ số khác nhau bằng cách lấy 04 chữ số từ tập hợp A gồm các phần tử là 1, 2, 3, 4, 5, 6, 7 và sắp xếp chúng theo một thứ tự cụ thể. Mỗi số này được coi là một chỉnh hợp chập 04 của 07 phần tử.
Do đó, số lượng các số tự nhiên có thể tạo ra từ tập hợp trên là 840 số.
Công thức tính tổ hợp
Khi nói đến công thức tổ hợp, chỉnh hợp, chúng ta sẽ có công thức tính tổ hợp chập “k” của số lượng “n” phần tử (1≤ k ≤ n) là:
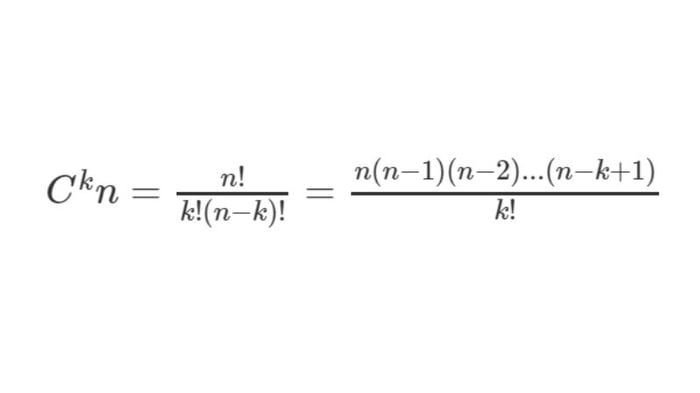
Trong trường hợp k > n, giá trị của “kn” sẽ là 0.
Ví dụ minh họa: Ông B có 11 người tham gia, muốn mời 05 người đi ăn. Trong số này, có 02 người không muốn tham gia. Ông B có bao nhiêu cách để mời?
Đáp án:
Ông B chọn một trong hai người này và thêm 4 người từ 9 người còn lại. Tổng cộng có:
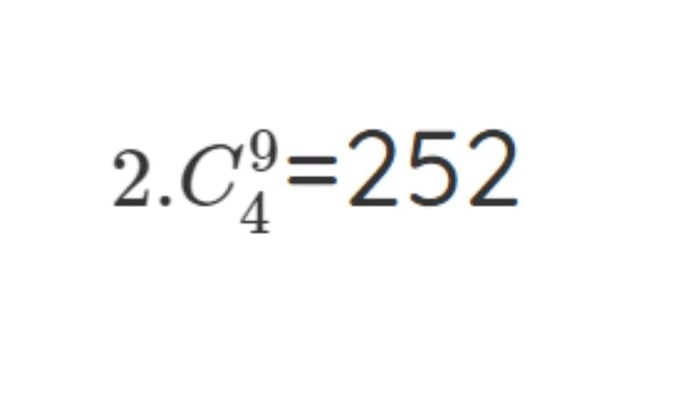
Ông B không mời hai người kia và chỉ mời 5 người từ chín người còn lại. Số cách là:
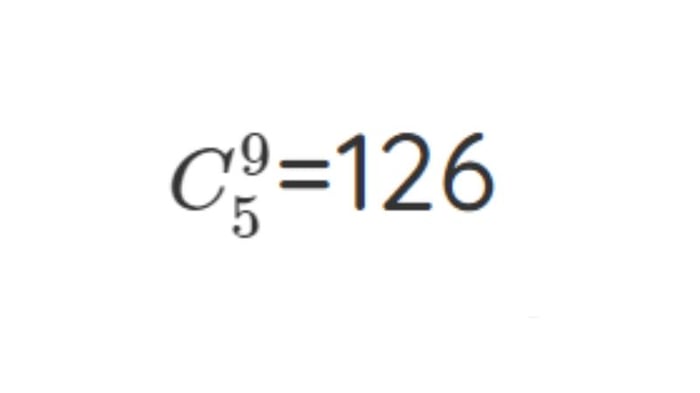
Tổng cộng, ông B sẽ có 328 cách để mời.
Công thức tính toán hoán vị
Để tính hoán vị của số lượng “n” phần tử (với n > 0), chúng ta sử dụng công thức:
Pn=n!
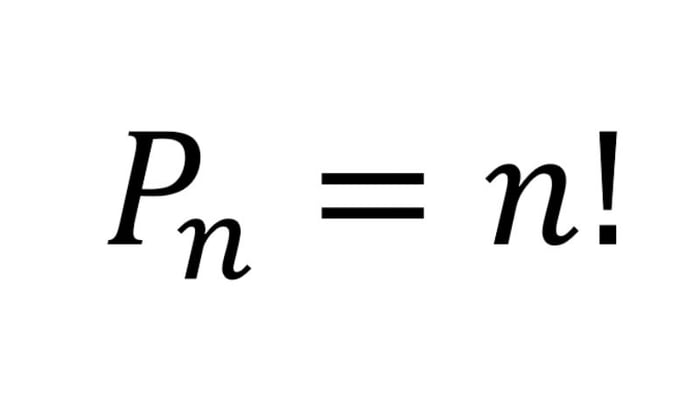
Bài tập ví dụ 1: Cho tập hợp A gồm 5 số là 3, 4, 5, 6, 7. Có bao nhiêu số tự nhiên khác nhau có thể được tạo ra từ tập hợp này?
Đáp án: Áp dụng công thức hoán vị Pn = n!. Vì vậy P5 = 5! và kết quả là 120 số.
Bài tập ví dụ 2: Hãy tính số cách sắp xếp 10 bạn thành một hàng theo chiều dọc?
Đáp án:
Sắp xếp 10 bạn thành một hàng theo chiều dọc là một loại hoán vị của 10 phần tử. Do đó, số cách sắp xếp 10 bạn thành một hàng dọc là P10 = 10!
Mối liên hệ giữa chỉnh hợp, tổ hợp và hoán vị trong toán học
Qua định nghĩa và các công thức về tổ hợp, chỉnh hợp, hoán vị ở trên, chúng ta có thể thấy chúng có mối quan hệ mật thiết với nhau. Cụ thể, một chỉnh hợp chập “k” của “n” phần tử có thể được xây dựng bằng cách thực hiện hai bước sau:
- Bước 1: Lựa chọn một tổ hợp chập “k” của “n” phần tử.
- Bước 2: Thực hiện hoán vị trên “k” phần tử đã chọn.
Do đó, chúng ta có thể biểu thị mối liên hệ giữa tổ hợp, chỉnh hợp và hoán vị bằng công thức sau:
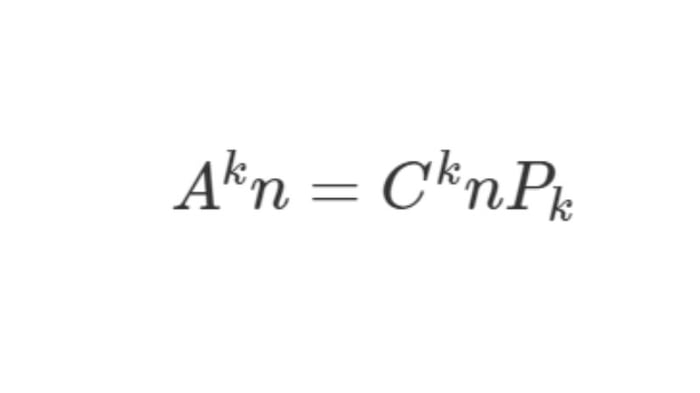
Quy tắc đếm chỉnh hợp, tổ hợp, hoán vị chính xác
Ngoài các công thức tổ hợp, chỉnh hợp, học sinh nên nắm rõ các quy tắc đếm chỉnh hợp, tổ hợp, hoán vị chính xác như sau:
Quy tắc áp dụng để đếm các tổ hợp
Chúng ta có một tập hợp A gồm n phần tử với điều kiện n > 0. Do đó, một tổ hợp chập “k” ngẫu nhiên của các phần tử từ tập A sẽ là một tập con gồm k phần tử của A, trong đó 0 ⩽ k ⩽ n ; k ∈ N.
Do đó, số lượng tổ hợp được tính bằng công thức sau: n!(n-k)!
Quy tắc để tính toán các chỉnh hợp
Chúng ta có một tập A gồm n phần tử với n ⩾ 1. Vì vậy, một chỉnh hợp chập “k” phần tử phân biệt thuộc A. Ở đây có 1 ⩽ k ⩽ n, k ∈ N.
Do đó, số lượng chỉnh hợp được tính bằng công thức sau: n!k!(n-k)!
Quy tắc đếm số hoán vị
Với một tập hợp gồm n phần tử phân biệt, chúng ta có thể lập được một hoán vị của r phần tử lấy ra từ tập hợp như sau:
- Lấy phần tử thứ nhất, có tổng cộng n cách;
- Lấy phần tử thứ hai, có n-1 cách sắp xếp hoán vị;
- ….
Tương tự, khi lấy phần tử thứ r trong tập hợp, có r-1 cách sắp xếp hoán vị:
- Trường hợp r = n, số lượng hoán vị khác nhau được tính bằng công thức P(n) = n!
- Trường hợp r < n, số hoán vị được tính bằng công thức P(n,r) = n!(n-r)!
Ví dụ minh họa về công thức tổ hợp, chỉnh hợp, hoán vị
Sau khi hiểu rõ công thức tổ hợp, chỉnh hợp, hoán vị, các bạn có thể xem ví dụ sau:
Ví dụ 1
Đề thi môn toán của lớp 12 tại một trường THPT gồm 12 đề tự luận và 15 đề trắc nghiệm. Mỗi học sinh khi dự thi phải làm 1 đề tự luận và 1 đề trắc nghiệm. Hỏi có bao nhiêu cách để mỗi học sinh chọn đề thi?
Giải:
Số cách chọn một đề tự luận là: 12 cách và số cách chọn một đề trắc nghiệm là 15 cách. Vậy tổng số cách để chọn đề thi là 12 x 15 = 180 cách.
Bài tập 2
Cho tập hợp A gồm các chữ số 1, 2, 3, 5, 7, 9:
a. Từ tập hợp trên có thể lập được bao nhiêu số tự nhiên khác nhau gồm 04 chữ số, mỗi số các chữ số đôi một khác nhau?
b. Từ tập hợp trên, có thể thiết lập được bao nhiêu số tự nhiên chẵn gồm 05 chữ số, mỗi số đều khác nhau lẫn nhau.
Giải pháp:
a. Chúng ta gọi số tự nhiên 04 chữ số là n = a1a2a3a4. Để có được số n như vậy, chúng ta cần chọn đồng thời các số a1, a2, a3, a4. Chúng ta có:
- a1 có tổng cộng 6 cách để chọn.
- a2 có tổng cộng 5 cách để chọn.
- a3 có tổng cộng 4 cách để chọn.
- a4 có tổng cộng 3 cách để chọn.
Vậy chúng ta có tổng cộng: 6 x 5 x 4 x 3 = 360 số n cần tìm.

b. Chúng ta xem xét số tự nhiên chẵn gồm 05 số là n = a1a2a3a4a5. Trong đó có:
- a5 chỉ có 1 cách chọn là 2.
- a1 có tổng cộng 5 cách để chọn.
- a2 có tổng cộng 4 cách để chọn.
- a3 có tổng cộng 3 cách để chọn.
- a4 có tổng cộng 2 cách để chọn.
Vậy tổng số n cần tìm là 1 x 2 x 3 x 4 x 5 = 120 số.
Bài tập 3
Cho tập hợp A chứa các số 0, 1, 2, 3, 4, 5, 6. Từ tập hợp này có thể tạo ra bao nhiêu số tự nhiên gồm 05 chữ số, mỗi số đều khác nhau và đảm bảo số 5 và số 2 không đứng cạnh nhau.
Giải pháp:
- Tìm ra các số tự nhiên gồm 05 chữ số khác nhau một cách tùy ý:
Số tự nhiên gồm 05 chữ số khác nhau với đảm bảo mỗi cặp số tùy ý có dạng n = a1a2a3a4a5. Trong đó:
- a1 có tổng cộng 6 cách để lựa chọn (a1 ≠ 0).
- a2 có tổng cộng 6 cách để lựa chọn.
- a3 có tổng cộng 5 cách để lựa chọn.
- a4 có tổng cộng 4 cách để lựa chọn.
- a5 có tổng cộng 3 cách để lựa chọn.
Do đó chúng ta có tổng cộng là 6 x 6 x 5 x 4 x 3 = 2169 số tự nhiên.
- Tìm ra số tự nhiên gồm 05 chữ số khác nhau từng đôi một và đảm bảo số 2 và số 5 không đứng cạnh nhau:
Giả sử có một chữ số ngẫu nhiên a là số 2 hoặc 5. Chúng ta sẽ tìm số tự nhiên có 04 chữ số:
Trường hợp 1: a1 = a
- a1 có tổng cộng 5 cách để lựa chọn.
- a2 có tổng cộng 4 cách để lựa chọn.
- a4 có tổng cộng 3 cách để lựa chọn.
Do đó chúng ta sẽ có 5 x 4 x 3 = 60 số.
Trường hợp 2: a1 ≠ a vì vậy:
- a1 có tổng cộng 4 cách để lựa chọn (vì a1 ≠ 0, 2, 5).
- Giả sử a2 = a thì có 3 vị trí cho số a.
- a3 có tổng cộng 4 cách để lựa chọn.
- a4 có tổng cộng 3 cách để lựa chọn.
Vậy chúng ta sẽ có 4 x 3 x 4 x 3 = 204. Với khả năng hoán đổi vị trí giữa số 2 và số 5, số lượng số sẽ là: 204 x 2 = 408.
Theo yêu cầu bài toán, ta có: 2160 – 408 = 1572 cách.
Qua các bài tập trên, các bạn có thể hiểu cách áp dụng các công thức toán học. Đây là những công thức tính chỉnh hợp, tổ hợp, hoán vị trong các bài toán cụ thể. Nhờ đó, các bạn có thể làm bài nhanh chóng và hấp thụ kiến thức hiệu quả hơn.
Các công thức tổ hợp, chỉnh hợp và hoán vị là những kiến thức cơ bản trong chương trình THPT. Chúng thường xuất hiện trong đề thi tốt nghiệp THPT qua nhiều năm. Vì vậy, học sinh cần nắm vững các công thức này để chuẩn bị tốt cho kỳ thi quan trọng.
