Tổng hợp đầy đủ các công thức Toán lớp 9 trong cả năm học

1. Tóm lược toàn bộ công thức Toán lớp 9 về Đại số

a) Căn bậc hai

- Các công thức cơ bản về căn bậc hai

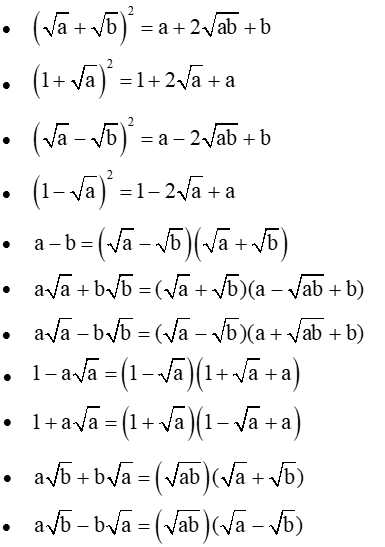
- Các điều kiện để căn thức có giá trị xác định

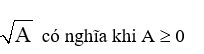
- Các điều kiện để các biểu thức có nghĩa

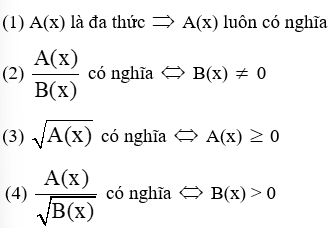
- Các đặc điểm của căn bậc 2

+ Đối với hai số a và b, với a, b > 0, ta có:

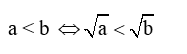
- Các công thức chuyển đổi căn thức

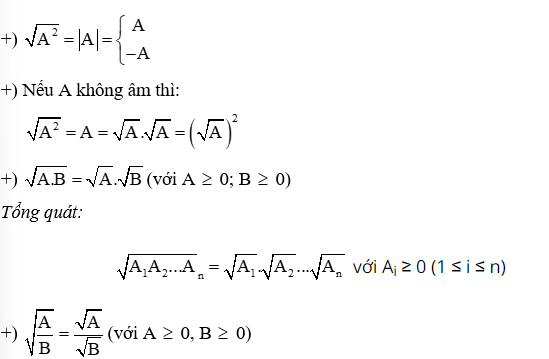
+ Đưa yếu tố A2 ra ngoài dấu căn bậc hai sẽ có:

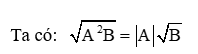
+ Đưa yếu tố vào trong dấu căn bậc hai:

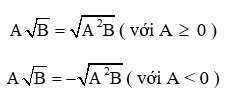
+ Khử mẫu trong biểu thức dưới dấu căn bậc hai:

Nhân mẫu số với yếu tố phụ để đạt được mẫu số dưới dạng bình phương:

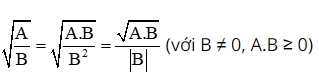
+ Đưa căn thức ra khỏi mẫu số

Dạng 1: Mẫu là biểu thức có dạng tích của các căn thức và số, thực hiện nhân cả tử lẫn mẫu với căn thức:

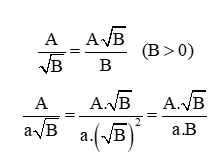
Dạng 2: Mẫu số là biểu thức tổng có căn thức, cần nhân cả tử và mẫu với biểu thức liên hợp của mẫu số.

- Phương trình có chứa căn bậc hai

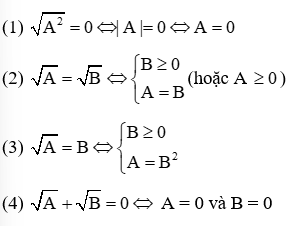
b) Căn bậc ba

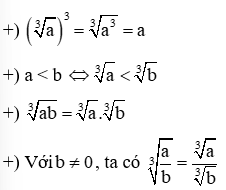
c) Hàm số bậc nhất

- Khái niệm về hàm số bậc nhất

+ Hàm số bậc nhất có dạng y = ax + b, với a và b là các số cố định và a khác 0.

- Tính chất: Hàm số bậc nhất y = ax + b xác định cho mọi giá trị x thuộc R và có các đặc điểm sau:

+ Hàm số đồng biến trên R khi a > 0

+ Hàm số nghịch biến trên R khi a < 0

- Đồ thị của hàm số y = ax + b (với a ≠ 0) là một đường thẳng

+ Cắt trục tung tại điểm có tọa độ y bằng b

+ Song song với đường thẳng y = ax nếu b ≠ 0, hoặc trùng với đường thẳng y = ax nếu b = 0

* Hướng dẫn vẽ đồ thị hàm số y = ax + b (với a ≠ 0)

Bước 1. Đặt x = 0, ta có y = b, nên điểm P(0; b) nằm trên trục tung Oy.

Đặt y = 0, ta tính được x = -b/a, dẫn đến điểm Q(-b/a; 0) nằm trên trục hoành Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q để có được đồ thị của hàm số y = ax + b.

- Mối quan hệ vị trí giữa hai đường thẳng

Xét hai đường thẳng (d): y = ax + b (với a ≠ 0) và (d’): y = a’x + b’ (với a’ ≠ 0). Khi đó:

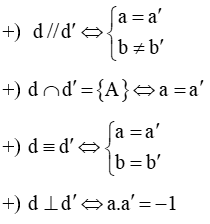
d) Hệ số góc của đường thẳng y = ax + b (với a ≠ 0)

* Góc tạo bởi đường thẳng y = ax + b với trục Ox. - Góc tạo bởi đường thẳng y = ax + b với trục Ox là góc giữa tia Ax và tia AT, trong đó A là điểm giao của đường thẳng y = ax + b với trục Ox, còn T là điểm thuộc đường thẳng y = ax + b.

* Hệ số góc của đường thẳng y = ax + b

- Hệ số a trong phương trình y = ax + b được gọi là hệ số góc của đường thẳng y = ax + b

e) Một số dạng phương trình đường thẳng

- Đường thẳng đi qua điểm M0(x0; y0) và có hệ số góc k có dạng: y = k(x – x0) + y0

- Đường thẳng đi qua điểm A(x0, 0) và B(0; y0) với x0.y0 ≠ 0 có phương trình x/x0 + y/y0 = 1

f) Công thức tính tọa độ trung điểm và độ dài của đoạn thẳng

Chohai điểm phân biệt A và B, với tọa độ A(xA, yA) và B(xB, yB). Khi đó

- Để tính độ dài đoạn thẳng AB, ta sử dụng công thức

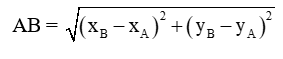
- Tọa độ trung điểm M của đoạn AB có thể tính bằng công thức

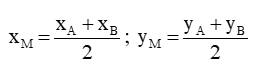
2. Tóm tắt toàn bộ công thức toán lớp 9 về phần Hình học

a) Các hệ thức lượng trong tam giác vuông

Xét tam giác ABC với đường cao AH

Gọi BC = a; AC = b; AB = c; AH = h; CH = b';

BH = c' và CH là các hình chiếu của AB và AC lên BC.

Chúng ta có các hệ thức sau đây:

+) b² = ab' ; c² = ac'

+) h² = b'c'

+) ah = bc

+) a² = b² + c² (Theo định lý Py-ta-go)

+) 1/ h² = 1/ b² + 1/ c²

b) Các tỉ số lượng giác của góc nhọn

- Khái niệm cơ bản

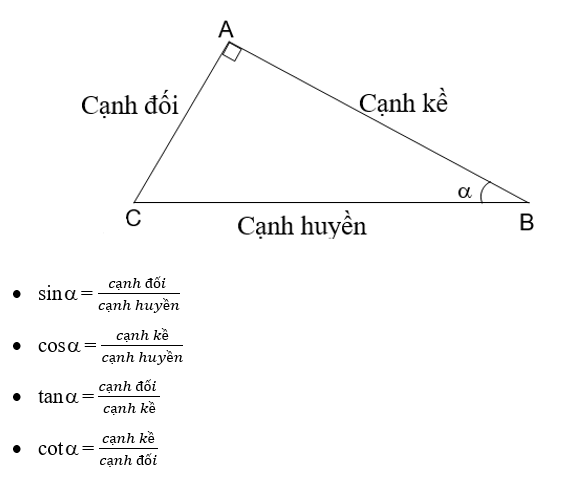
- Các tính chất quan trọng

- Các tỉ số lượng giác của những góc đặc biệt

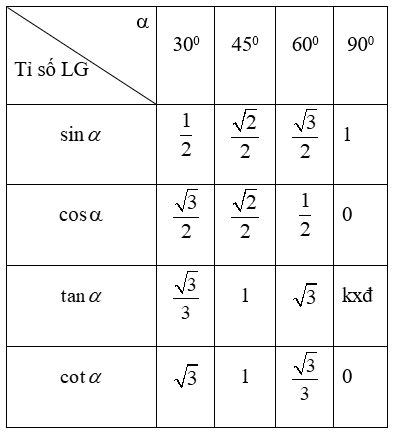
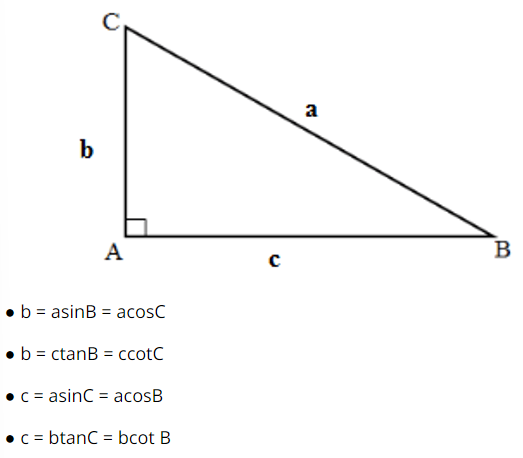
c) Các hệ thức liên quan đến cạnh và góc trong tam giác vuông

3. Một số bài tập cùng đáp án chi tiết

Bài 1: Chuyển đổi các biểu thức sau thành bình phương của biểu thức khác:

a) 4 - 2√3

b) 7 + 4√3

c) 13 - 4√3

Hướng dẫn cách giải:

a) 4 - 2√3 = 3 - 2√3 + 1 = (√3 - 1)²

b) 7 + 4√3 = 4 + 2 × 2 × √3 + 3 = (2 + √3)²

c) 13 - 4√3 = (2√3)² - 2 × 2 × √3 + 1 = (2√3 - 1)²

Bài 2: Đơn giản hóa biểu thức

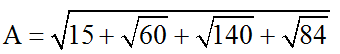
Hướng dẫn chi tiết:

  Phân tích biểu thức:

Chúng ta chú ý rằng:

√60 = 2√15 = 2√5 × √3

√140 = 2√35 = 2√5 × √7

√84 = 2√21 = 2√7 × √3

Và 15 = 3 + 5 + 7.

Chúng ta nhận thấy hình dạng của hằng đẳng thức: a² + b² + c² + 2ab + 2bc + 2ca = (a + b + c)² Giải thích:

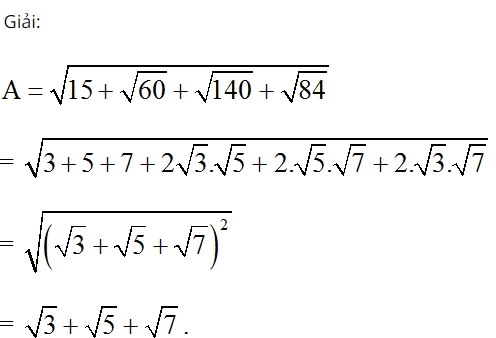
Bài 3: Xác định giá trị của x để biểu thức A dưới đây bằng 2

Cách giải: Tìm giá trị của x sao cho biểu thức đạt giá trị thỏa mãn các đẳng thức và bất đẳng thức

Phương pháp giải quyết

a) Xác định điều kiện của x để biểu thức A < m (hoặc A > m ; A ≥ m ; A ≤ m)

+ Xác định điều kiện có thể xảy ra

  + Đơn giản hóa biểu thức (nếu cần) +

Chuyển đổi điều kiện A < m để tìm giá trị của x.

Lưu ý: Khi nhân (chia) cả hai vế của bất phương trình với một biểu thức > 0, chiều của bất phương trình không thay đổi.

b) Xác định điều kiện của x để hàm số đạt giá trị cực đại hoặc cực tiểu

  + Xác định điều kiện hợp lệ

  + Đơn giản hóa biểu thức (nếu cần).

+ Sử dụng bất đẳng thức để đánh giá biểu thức ≤ k (tìm giá trị lớn nhất) hoặc ≥ k (tìm giá trị nhỏ nhất) (k là hằng số)

+ Tìm x để biểu thức đạt dấu =.

Lưu ý: Bất đẳng thức Cô-si: a² + b² ≥ 2ab

A² luôn lớn hơn hoặc bằng 0 với mọi giá trị của A.

Hướng dẫn giải:

Điều kiện xác định: x > 0 hoặc x = 0

Chúng ta có: 

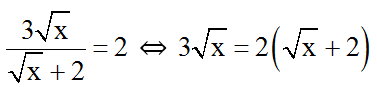
3√x = 2√x + 4

⇔ √x = 4

⇔ x = 16

Do đó, x = 16

Bài 4: Không sử dụng máy tính, hãy so sánh các giá trị sau:

1. 8 và √65.

2. √15 - 1 và √10

3. 3√3 - 2√2 và 2

4. 3√12 và 2√26

5. So sánh 4 - 2√2 và 3 - √3

Phương pháp giải:

Dựa vào quy tắc: Nếu a, b ≥ 0 thì a < b tương đương với √a < √b

Hướng dẫn giải

1. Chúng ta có 8 = √64. Vì √64 nhỏ hơn √65 nên 8 nhỏ hơn √65.

2. Chúng ta có √15 - 1 nhỏ hơn √16 - 1, tức là 4 - 1 = 3. Trong khi đó, √10 lớn hơn √9, tức là 3.

Do đó, √15 - 1 nhỏ hơn √10.

3. Ta có 3√3 lớn hơn 2√2, do đó 3√3 - 2√2 lớn hơn 0 và 2 cũng lớn hơn 0.

Giả sử 3√3 - 2√2 lớn hơn 2, thì (3√3 - 2√2)² phải lớn hơn 2², tức là 35 - 12√6 phải lớn hơn 4, từ đó 31 phải lớn hơn 12√6, dẫn đến √961 phải lớn hơn √864.

4. Giả sử 3√12 lớn hơn 2√26, điều này tương đương với √108 lớn hơn √104 (bất đẳng thức này là đúng).

Vậy, ta có 3√12 lớn hơn 2√26.

Giả sử 4 - 2√2 lớn hơn 3 - √3.

⇔ 4 - 3 lớn hơn 2√2 - √3 ⇔ 1 lớn hơn 2√2 - √3.

Vì 2√2 = 8 lớn hơn √3, nên: 2√2 - √3 lớn hơn 0.

Do đó, 12 lớn hơn (2√2 - √3)².

⇔ 1 lớn hơn 11 - 4√6

⇔ 4√6 lớn hơn 10

⇔ √96 lớn hơn √100 (bất đẳng thức không đúng).

Vậy, 4 - 2√2 nhỏ hơn 3 - √3.

Bài 5: Trong tam giác vuông ABC tại A với đường cao AH, tính cạnh BC biết rằng AB = 15 cm và HC = 16 cm.

Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:

AC² = CH. BC = 16. BC

AB² + AC² = BC²

⇔ 152 + 16. BC = BC²

⇔ BC² - 16. BC - 225 = 0

⇔ BC² - 25. BC + 9. BC - 225 = 0

⇔ BC. (BC - 25) + 9. (BC - 25) = 0

⇔ (BC - 25). (BC + 9) = 0

⇔ BC = 25 hoặc BC = -9 (bỏ qua)

=> AC² = 16.BC = 16. 25 = 400

=> AC = 20

+ Trong tam giác vuông ABC, áp dụng hệ thức lượng: AH. BC = AB.AC

Kết quả: BC = 25 cm và AC = 20 cm

Trên đây là một số thông tin liên quan đến công thức toán lớp 9, bao gồm công thức đại số và hình học. Để tìm hiểu chi tiết hơn về các nội dung trên, vui lòng tham khảo: Lý thuyết Chương 1: Hệ thức lượng trong tam giác vuông | Lý thuyết Toán 9. Trân trọng !