1. Tổng hợp kiến thức hình học lớp 8 học kỳ 1 - chương I về hình học
Hình tứ giác:
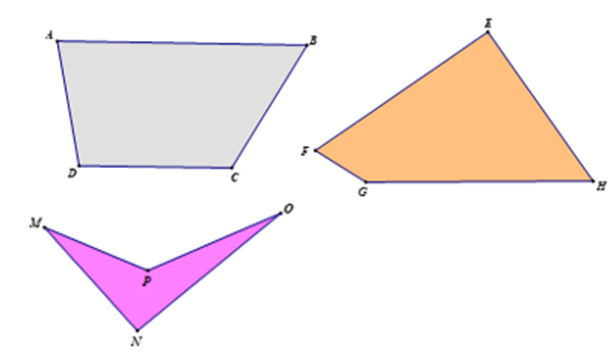
- Tứ giác ABCD là hình có bốn đoạn thẳng AB, BC, CD, DA, trong đó không có hai đoạn thẳng nào nằm chung trên một đường thẳng.
- Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng được giới hạn bởi đường thẳng chứa bất kỳ cạnh nào của nó. (Ngược lại là tứ giác lõm)
- Định lý: Tổng của các góc trong một tứ giác là 360°
- Góc ngoài của tứ giác là góc kề bù với một góc trong của tứ giác. Tổng các góc ngoài của tứ giác cũng bằng 360°
Hình thang:
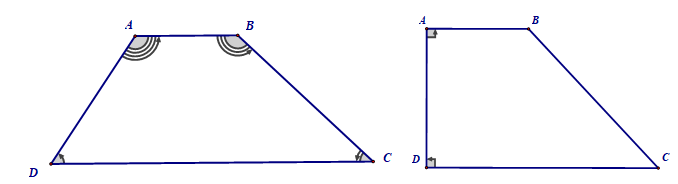
Hình thang ABCD có các đặc điểm sau:
- AB // CD
- Nếu ABCD là hình thang, thì ABCD là hình thang vuông
Hình thang cân:
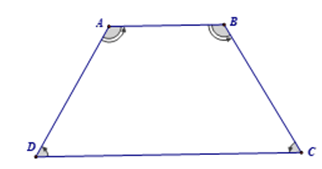
- Hình thang cân là loại hình thang có hai góc kề một đáy bằng nhau.
- Hai góc đối diện của hình thang cân có tổng bằng 180°
- Đặc điểm: Trong hình thang cân ABCD, ta có AD = BC và AC = BD
- Dấu hiệu nhận diện
+ Tứ giác ABCD là hình thang cân
+ Tứ giác ABCD là hình thang cân
+ Tứ giác ABCD là hình thang cân
Đường trung bình của tam giác và hình thang:
- Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm của hai cạnh của tam giác.
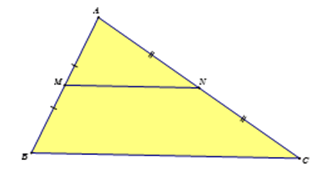
+ Trong tam giác ABC, đoạn MN là đường trung bình của tam giác
+ Đoạn MN là đường trung bình của tam giác ABC
- Đường trung bình của hình thang: Là đoạn thẳng nối hai trung điểm của hai cạnh bên trong hình thang.
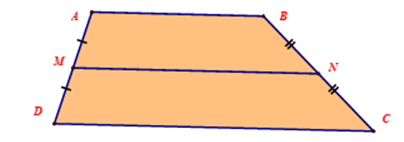
+ Trong hình thang ABCD, MN đóng vai trò là đường trung bình của hình thang này
+ Nếu MN là đường trung bình của hình thang ABCD thì
Đối xứng qua trục:
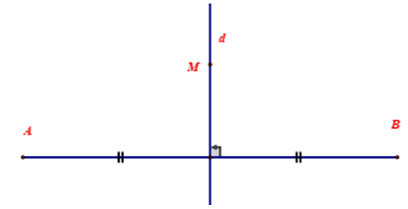
- Hai điểm A và B được gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối A và B.
- Quy tắc: Nếu điểm M nằm trên đường thẳng d, thì điểm đối xứng của M qua d cũng chính là điểm M.
- Hai hình được gọi là đối xứng qua đường thẳng d nếu mọi điểm của hình này đối xứng với một điểm của hình kia qua d, và ngược lại. Đường thẳng d được gọi là trục đối xứng của hai hình đó.
- Nếu hai đoạn thẳng (hoặc góc, tam giác) đối xứng qua một đường thẳng, thì chúng sẽ bằng nhau.
- Đường thẳng d được gọi là trục đối xứng của hình H nếu điểm đối xứng của mọi điểm thuộc H qua d vẫn thuộc hình H. Ta nói hình H có trục đối xứng.
- Đường thẳng đi qua trung điểm của hai đáy trong hình thang cân chính là trục đối xứng của hình thang cân đó.
Hình bình hành:
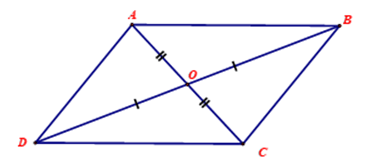
- Hình bình hành là một tứ giác với các cạnh đối diện song song.
- Hình bình hành là một dạng đặc biệt của hình thang (hình bình hành là hình thang với hai cạnh bên song song).
Đối xứng qua tâm:
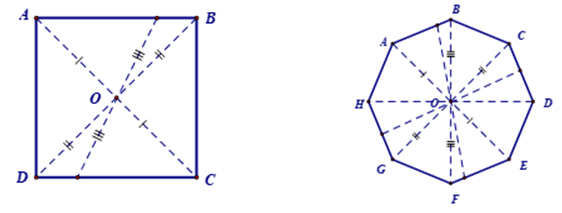
- Hai điểm A và B được coi là đối xứng qua điểm O nếu O là trung điểm của đoạn thẳng nối A và B. (Lưu ý: Điểm đối xứng của điểm O qua chính O cũng là điểm O.)
- Hai hình được gọi là đối xứng qua điểm O nếu mọi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua O và ngược lại. Điểm O là tâm đối xứng của hai hình đó.
- Nếu hai đoạn thẳng (hoặc góc, tam giác) đối xứng qua một điểm thì chúng sẽ bằng nhau.
- Điểm O được gọi là tâm đối xứng của hình H nếu mọi điểm đối xứng của hình H qua O cũng nằm trong hình H. Ta nói hình H có tâm đối xứng.
- Điểm giao nhau của hai đường chéo trong hình bình hành chính là tâm đối xứng của hình bình hành đó.
Hình chữ nhật:
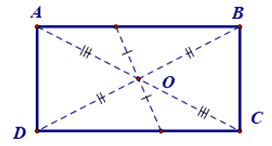
- Hình chữ nhật là một tứ giác có bốn góc vuông.
- Theo định nghĩa về hình chữ nhật, ta có thể thấy rằng hình chữ nhật cũng đồng thời là một hình bình hành và một hình thang cân.
Các đặc điểm:
+ Hình chữ nhật sở hữu toàn bộ các đặc điểm của hình bình hành và hình thang cân.
+ Dựa vào đặc điểm của hình thang cân và hình bình hành: Trong hình chữ nhật, hai đường chéo có độ dài bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Dấu hiệu nhận diện:
+ Một tứ giác có ba góc vuông là hình chữ nhật.
+ Nếu hình thang cân có một góc vuông, thì đó là hình chữ nhật.
+ Một hình bình hành có một góc vuông sẽ là hình chữ nhật.
+ Nếu hình bình hành có hai đường chéo bằng nhau, thì nó là hình chữ nhật.
Hình thoi:
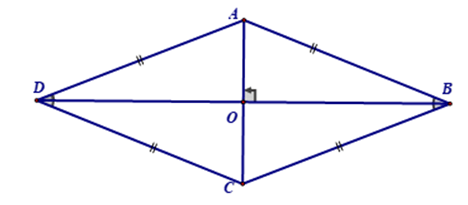
Hình thoi là một tứ giác với bốn cạnh đều nhau và đồng thời là hình bình hành.
- Đặc điểm: Hình thoi mang tất cả các đặc tính của hình bình hành.
ABCD là một hình thoi.
- Dấu hiệu nhận diện:
+ Tứ giác có tất cả bốn cạnh bằng nhau chính là hình thoi.
+ Một hình bình hành với hai cạnh kề bằng nhau sẽ là hình thoi.
+ Hình bình hành có hai đường chéo cắt nhau vuông góc chính là hình thoi.
+ Nếu một đường chéo của hình bình hành là đường phân giác của một góc, thì hình đó là hình thoi.
Hình vuông:
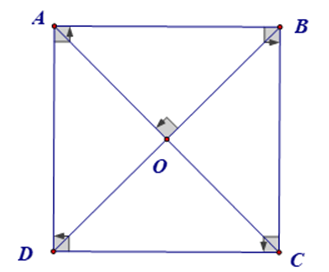
- Hình vuông là tứ giác có bốn góc vuông và tất cả bốn cạnh đều bằng nhau.
- Dựa vào định nghĩa về hình vuông, ta có thể rút ra:
+ Hình vuông là một hình chữ nhật với tất cả bốn cạnh bằng nhau.
+ Hình vuông cũng là một hình thoi với một góc vuông.
+ Vì vậy, hình vuông đồng thời là cả hình chữ nhật và hình thoi.
- Các đặc điểm:
+ Hình vuông mang tất cả các đặc tính của hình chữ nhật và hình thoi.
+ Các đường chéo của hình vuông không chỉ bằng nhau mà còn cắt nhau vuông góc.
- Dấu hiệu nhận diện:
+ Một hình chữ nhật có hai cạnh kề bằng nhau sẽ là hình vuông.
+ Hình vuông là hình chữ nhật với hai đường chéo cắt nhau tạo góc vuông
+ Hình vuông là hình chữ nhật có một đường chéo trùng với đường phân giác của góc
+ Hình vuông là hình thoi có một góc vuông
+ Hình vuông là hình thoi với hai đường chéo bằng nhau
2. Bài tập để củng cố kiến thức
Bài 1: Cho tam giác ABC. Từ trung điểm M của cạnh AB, kẻ đường MP song song với BC và MN song song với AC (P thuộc AC và N thuộc BC).
a) Chứng minh rằng các tứ giác MNCP và BMPN là hình bình hành.
b) Gọi I là giao điểm của MN và BP, Q là giao điểm của MC và PN. Chứng minh rằng IQ bằng 1/2 MP.
c) Xác định điều kiện để tứ giác BMPN trở thành hình chữ nhật trong tam giác ABC.
Bài 2: Cho hình chữ nhật ABCD, với hai đường chéo AC và BD giao nhau tại điểm O.
a) Cho AB = 4cm, BC = 3cm. Tính các độ dài của BD và AO.
b) Vẽ đường AH vuông góc với BD. Đặt M, N, I lần lượt là trung điểm của AH, DH, BC. Chứng minh rằng MN bằng BI.
c) Chứng minh rằng BM song song với IN.
d) Chứng minh rằng góc ANI là góc vuông.
Bài 3: Trong tam giác ABC (AB < AC) có đường cao AH. Xác định M, N, K là các trung điểm của AB, AC, BC.
a) Chứng minh rằng tứ giác BCMN là hình thang.
b) Chứng minh rằng tứ giác AMKN là hình bình hành.
c) Xác định điểm D là điểm đối xứng của H qua M. Chứng minh rằng tứ giác ADBH là hình chữ nhật.
d) Xác định điều kiện để tứ giác AMKN trở thành hình vuông trong tam giác ABC.
Bài 4: Cho tam giác ABC vuông tại A (AB < AC), với đường cao AH. O là trung điểm của BC và D là điểm đối xứng của A qua O.
a) Chứng minh rằng tứ giác ABDC là hình chữ nhật.
b) Trên tia đối của tia HA, đặt điểm E sao cho HE = HA. Chứng minh rằng cả tam giác AED và tam giác BEC đều vuông góc.
c) Gọi M, N lần lượt là hình chiếu của E lên BD và CD, với EM cắt AD tại K. Chứng minh DE bằng DK.
d) Chứng minh rằng ba điểm H, M, N nằm trên cùng một đường thẳng.
3. Phương pháp học và ôn tập Toán lớp 8 hiệu quả.
Chương trình Toán lớp 8 cung cấp nhiều kiến thức nền tảng quan trọng. Học sinh cần nắm vững những kiến thức này để giải quyết các bài tập về hệ phương trình và hình học ở các lớp học cao hơn, đặc biệt là chuẩn bị cho kỳ thi vào lớp 10. Bên cạnh việc ôn tập với tài liệu Tổng hợp kiến thức toán 8, những lưu ý dưới đây sẽ giúp các em học toán 8 hiệu quả hơn.
- Để giải toán lớp 8 một cách chính xác, các em cần củng cố kiến thức từ các lớp học trước. Nếu còn thiếu sót, hãy nhanh chóng bổ sung. Việc học toán khi kiến thức nền tảng chưa vững sẽ gây khó khăn và không đạt hiệu quả cao.
- Tránh lạm dụng sách giải mẫu toán lớp 8. Việc tham khảo quá nhiều sách giải sẽ làm giảm khả năng tư duy toán học và khiến học sinh phụ thuộc vào các cách giải mẫu.
- Học cách sử dụng máy tính cầm tay một cách hợp lý, không nên quá phụ thuộc vào nó trong quá trình giải bài tập.
- Trong quá trình nghe giảng, nếu gặp phần kiến thức chưa rõ, hãy chủ động hỏi giáo viên hoặc bạn bè ngay lập tức. Đảm bảo luôn hiểu và nắm vững kiến thức từ những buổi học đầu tiên.
- Hãy chủ động tìm nhiều cách giải khác nhau cho mỗi bài toán. Tuy nhiên, nên giải bài một cách cẩn thận và đầy đủ từng bước để nắm vững quy trình. Sau khi đã quen thuộc với phương pháp, bạn có thể giải nhanh hơn.
- Bên cạnh việc ôn tập kiến thức toán 8, học sinh cần dành thời gian cho các hoạt động thể thao để rèn luyện sức khỏe. Việc không chăm sóc sức khỏe và học tập khi mệt mỏi sẽ không đạt hiệu quả cao.
