| Một phần của chuỗi bài viết về |
| Cơ học cổ điển |
|---|
Định luật 2 của Newton về chuyển động |
|
|
Các nhánh[hiện] |
|
Động học chất điểm[hiện] |
|
Động lực học chất điểm[hiện] |
|
Năng lượng và Bảo toàn năng lượng[hiện] |
|
Cơ học vật rắn[hiện] |
|
Hệ hạt và Tương tác hạt[hiện] |
|
Dao động cơ và Sóng cơ[hiện] |
|
Các nhà khoa học[hiện] |
|
| Thuyết tương đối rộng |
|---|
|
Dẫn nhập · Lịch sử · Nguyên lý toán học Kiểm chứng |
|
Khái niệm cơ sở[hiện] |
|
Hiệu ứng và hệ quả[hiện] |
|
Phương trình[hiện] |
|
Lý thuyết phát triển[hiện] |
|
Các nghiệm[hiện] |
|
Nhà vật lý[hiện] |
|
Không–thời gian[hiện] |
Trong lĩnh vực vật lý, lực hấp dẫn, hay chính xác hơn là tương tác hấp dẫn, là một hiện tượng tự nhiên khiến mọi vật thể có khối lượng hoặc năng lượng - từ các hành tinh, ngôi sao, thiên hà đến cả ánh sáng - bị hút về nhau. Trên Trái Đất, lực hấp dẫn tạo ra trọng lượng cho các vật thể, và lực hấp dẫn của Mặt Trăng gây ra hiện tượng thủy triều. Nó cũng đóng vai trò quan trọng trong việc hình thành các ngôi sao và tập hợp chúng thành các thiên hà, vì vậy lực hấp dẫn chịu trách nhiệm cho nhiều cấu trúc lớn trong vũ trụ. Lực hấp dẫn có phạm vi vô hạn, mặc dù cường độ của nó giảm dần khi các vật thể cách xa nhau.
Lực hấp dẫn được mô tả rõ ràng nhất bằng lý thuyết tương đối tổng quát của Albert Einstein (được đề xuất vào năm 1915), cho rằng lực hấp dẫn không phải là một lực đơn thuần, mà là kết quả của độ cong của không-thời gian do sự phân bố khối lượng không đồng đều tạo ra. Ví dụ nổi bật về độ cong không-thời gian này là lỗ đen, nơi ngay cả ánh sáng cũng không thể thoát ra khi vượt qua chân trời sự kiện. Tuy nhiên, trong hầu hết các tình huống, lực hấp dẫn có thể được mô tả gần đúng theo định luật vạn vật hấp dẫn của Newton, coi lực hấp dẫn là một lực đơn giản kéo các vật thể lại gần nhau, với cường độ tỷ lệ thuận với sản phẩm khối lượng và tỷ lệ nghịch với bình phương khoảng cách giữa chúng.
Lực hấp dẫn là yếu nhất trong bốn tương tác cơ bản của vật lý, yếu hơn khoảng 10 lần so với tương tác mạnh, yếu hơn 10 lần so với lực điện từ và yếu hơn 10 lần so với tương tác yếu. Do đó, lực hấp dẫn không có ảnh hưởng đáng kể ở cấp độ các hạt hạ nguyên tử. Ngược lại, ở quy mô vĩ mô, lực hấp dẫn lại là tương tác nổi bật, đóng vai trò quan trọng trong việc hình thành, tạo hình và xác định quỹ đạo của các thiên thể.
Trong cơ học cổ điển, lực hấp dẫn được xem như một ngoại lực ảnh hưởng đến các vật thể. Ngược lại, trong thuyết tương đối rộng, lực hấp dẫn là kết quả của sự uốn cong không-thời gian bởi khối lượng, chứ không phải là một lực ngoại lai. Thuyết hấp dẫn lượng tử coi graviton là hạt truyền tải lực hấp dẫn.
Trong Vũ trụ, lực hấp dẫn có thể tồn tại dưới dạng hấp dẫn lượng tử, siêu trọng lực hoặc một điểm kỳ dị hấp dẫn. Giai đoạn này diễn ra trong kỷ nguyên Planck (khoảng 10 giây đầu tiên sau Vũ trụ hình thành) và có thể phát sinh từ trạng thái nguyên thủy như chân không giả, chân không lượng tử hoặc hạt ảo, theo cách chưa rõ. Việc phát triển lý thuyết hấp dẫn lượng tử, để kết hợp lực hấp dẫn với ba tương tác cơ bản khác trong vật lý, đang là một lĩnh vực nghiên cứu hiện tại.
Lịch sử lý thuyết hấp dẫn
Thế giới cổ đại
Triết gia Hy Lạp cổ đại Archimedes đã phát hiện trọng tâm của một hình tam giác. Ông cũng đưa ra nhận định rằng nếu hai vật có trọng lượng bằng nhau nhưng không có trọng tâm chung, thì trọng tâm của hai vật kết nối sẽ nằm trên đường nối giữa hai trọng tâm của chúng.
Vitruvius, kiến trúc sư và kỹ sư La Mã, trong tác phẩm De Architectura, đã khẳng định rằng trọng lực của một vật không phụ thuộc vào khối lượng của nó mà là thuộc về 'bản chất' của vật đó.
Tại Ấn Độ cổ đại, Aryabhata đã lần đầu tiên giải thích lý do tại sao các vật thể không bị ném ra ngoài khi Trái Đất quay. Brahmagupta đã mô tả trọng lực như một lực hấp dẫn và dùng thuật ngữ 'gurutvaakarshan' để chỉ lực này.
Cách mạng khoa học
Lý thuyết hấp dẫn hiện đại bắt đầu từ công trình của Galileo Galilei vào cuối thế kỷ 16 và đầu thế kỷ 17. Trong thí nghiệm nổi tiếng (dù có thể bị ngụy tạo) thả vật từ Tháp nghiêng Pisa, và sau đó là các phép đo chính xác của vật lăn trên mặt phẳng nghiêng, Galileo đã chỉ ra rằng gia tốc trọng trường là giống nhau cho tất cả các vật thể. Đây là sự thay đổi lớn so với quan niệm của Aristotle rằng các vật nặng hơn có gia tốc trọng trường cao hơn. Galileo cho rằng sự cản trở của không khí là lý do khiến các vật thể nhẹ hơn rơi chậm hơn trong khí quyển. Công trình của Galileo đã đặt nền móng cho sự phát triển của thuyết hấp dẫn Newton.
Thuyết hấp dẫn của Newton

Vào năm 1687, Sir Isaac Newton, một nhà toán học người Anh, đã công bố tác phẩm Principia, trong đó ông đưa ra giả thuyết về định luật nghịch đảo bình phương của trọng lực phổ quát. Newton viết: 'Tôi đã suy luận rằng lực giữ các hành tinh trong quỹ đạo của chúng phải tỷ lệ nghịch với bình phương khoảng cách từ các trung tâm mà chúng quay tròn: và do đó so sánh lực cần thiết để giữ Mặt trăng trong quỹ đạo với lực hấp dẫn trên bề mặt Trái Đất và nhận thấy chúng gần như tương đương.' Phương trình như sau:
Trong đó F đại diện cho lực, m1 và m2 là khối lượng của các vật thể tương tác, r là khoảng cách giữa các khối lượng, và G là hằng số hấp dẫn.
Lý thuyết của Newton đã đạt được thành công lớn khi dự đoán sự tồn tại của sao Hải Vương, dựa trên các chuyển động không thể giải thích của sao Thiên Vương bởi các hành tinh khác. Tính toán của John Couch Adams và Urbain Le Verrier đã xác định vị trí chung của hành tinh này, và tính toán của Le Verrier đã dẫn đến phát hiện sao Hải Vương bởi Johann Gottfried Galle.
Sự khác biệt trong quỹ đạo của sao Thủy đã chỉ ra những thiếu sót trong lý thuyết của Newton. Vào cuối thế kỷ 19, các nhà khoa học nhận thấy rằng quỹ đạo của sao Thủy có những nhiễu loạn nhỏ không thể hoàn toàn giải thích bằng lý thuyết của Newton. Các tìm kiếm cho một vật thể gây nhiễu loạn khác (như một hành tinh gần hơn quanh Mặt trời) đều không thành công. Vấn đề này đã được giải quyết vào năm 1915 nhờ thuyết tương đối rộng của Albert Einstein, tính toán sự khác biệt nhỏ trong quỹ đạo của sao Thủy. Sự khác biệt này thể hiện sự gia tăng tốc độ của sao Thủy với chênh lệch 42,98 giây cung mỗi thế kỷ.
Dù lý thuyết của Newton đã được thay thế bởi thuyết tương đối rộng của Albert Einstein, nhưng nhiều phép tính hấp dẫn không liên quan đến thuyết tương đối hiện đại vẫn sử dụng lý thuyết của Newton vì nó đơn giản hơn và cung cấp kết quả đủ chính xác cho hầu hết các ứng dụng có khối lượng, tốc độ và năng lượng nhỏ.
Nguyên lý tương đương
Nguyên lý tương đương, được khám phá bởi nhiều nhà nghiên cứu như Galileo, Loránd Eötvös và Einstein, thể hiện ý tưởng rằng tất cả các vật thể rơi theo cùng một cách và ảnh hưởng của trọng lực không thể phân biệt với các yếu tố của gia tốc và giảm tốc. Cách đơn giản nhất để kiểm tra nguyên lý tương đương yếu là thả hai vật có khối lượng hoặc thành phần khác nhau trong chân không và xem chúng có chạm đất cùng một lúc không. Các thí nghiệm như vậy cho thấy rằng tất cả các vật thể rơi với cùng một tốc độ khi các lực khác (như sức cản không khí và hiệu ứng điện từ) không đáng kể. Các thử nghiệm tinh vi hơn sử dụng cân bằng xoắn của Eötvös và các thí nghiệm vệ tinh như STEP được thiết kế để có kết quả chính xác hơn trong không gian.
Các công thức của nguyên lý tương đương bao gồm:
- Nguyên lý tương đương yếu: Quỹ đạo của một điểm khối lượng trong trường hấp dẫn chỉ phụ thuộc vào vị trí và vận tốc ban đầu của nó, không phụ thuộc vào các thành phần của khối lượng đó. [17]
- Nguyên lý tương đương của Einstein: Kết quả từ bất kỳ thí nghiệm rơi tự do nào trong phòng thí nghiệm, không liên quan đến hấp dẫn, đều không phụ thuộc vào vận tốc và vị trí của phòng thí nghiệm trong không-thời gian. [18]
- Nguyên lý tương đương mạnh bao gồm cả hai điều kiện trên.
Thuyết tương đối rộng
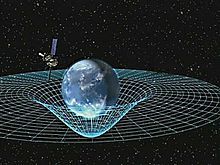
Trong thuyết tương đối rộng, trọng lực được quy cho độ cong của không-thời gian thay vì một lực. Nguyên lý tương đương là nền tảng cho thuyết tương đối rộng, so sánh sự rơi tự do với chuyển động quán tính và mô tả các vật thể quán tính rơi tự do khi gia tốc so với các quan sát viên không quán tính trên mặt đất. Trong vật lý Newton, gia tốc như vậy không thể xảy ra trừ khi ít nhất một vật thể chịu tác động của một lực.
Einstein đã chỉ ra rằng không-thời gian bị cong bởi vật chất, và các vật thể rơi tự do di chuyển theo các đường thẳng cục bộ trong không-thời gian cong, được gọi là trắc địa. Tương tự như định luật chuyển động đầu tiên của Newton, lý thuyết của Einstein cho rằng nếu một lực tác động lên một vật thể, nó sẽ lệch khỏi trắc địa. Ví dụ, chúng ta không theo dõi trắc địa khi đứng vì sức cản của Trái Đất tạo ra một lực hướng lên, làm chúng ta không có quán tính trên mặt đất. Điều này giải thích lý do di chuyển dọc theo trắc địa trong không-thời gian được coi là quán tính.
Einstein đã phát hiện các phương trình trường trong thuyết tương đối rộng, liên kết sự hiện diện của vật chất với độ cong của không-thời gian, và các phương trình này được đặt theo tên ông. Phương trình trường Einstein bao gồm 10 phương trình vi phân đồng thời, phi tuyến tính. Các nghiệm của phương trình này là các thành phần của thang đo hệ số không-thời gian, mô tả hình học của không-thời gian. Các đường trắc địa trong không-thời gian được xác định dựa trên thang đo hệ mét.
Cụ thể
Lực hấp dẫn của Trái Đất
Mỗi hành tinh, bao gồm cả Trái Đất, đều được bao quanh bởi trường hấp dẫn của riêng nó, có thể được lý giải bằng vật lý Newton như là một lực hấp dẫn tác động lên tất cả các vật thể. Đối với hành tinh hình cầu đối xứng, sức mạnh của trường hấp dẫn tại bất kỳ điểm nào trên bề mặt tỷ lệ thuận với khối lượng của hành tinh và tỷ lệ nghịch với bình phương khoảng cách từ tâm của hành tinh.
Độ mạnh của trường hấp dẫn được đo bằng gia tốc mà các vật thể chịu dưới ảnh hưởng của nó. Tốc độ gia tốc của các vật rơi gần bề mặt Trái Đất chỉ thay đổi chút ít tùy thuộc vào vĩ độ, các đặc điểm bề mặt như núi và dãy núi, cũng như có thể do sự biến đổi của mật độ bề mặt. Đối với khối lượng và thước đo, giá trị trọng lực tiêu chuẩn được quy định bởi Cục Trọng lượng và Đo lường Quốc tế theo Hệ thống Đơn vị Quốc tế (SI).
Giá trị này, ký hiệu là g = 9,80665 m/s² (32,1740 ft/s²).
Giá trị tiêu chuẩn 9,80665 m/s² được Ủy ban Quốc tế về Trọng lượng và Đo lường áp dụng từ năm 1901 cho vĩ độ 45°, mặc dù thực tế nó cao hơn khoảng năm phần nghìn. Giá trị này đã được sử dụng trong khí tượng học và một số tiêu chuẩn khí quyển cho vĩ độ 45°, mặc dù nó chính xác hơn cho vĩ độ 45°32'33'.
Nếu sử dụng giá trị chuẩn cho g và không tính đến sức cản của không khí, điều này có nghĩa là một vật rơi tự do gần bề mặt Trái Đất sẽ tăng tốc với vận tốc 9,80665 m/s (32,1740 ft/s hoặc 22 mph) mỗi giây. Do đó, một vật bắt đầu từ trạng thái nghỉ sẽ đạt vận tốc 9,80665 m/s (32,1740 ft/s) sau một giây, khoảng 19,62 m/s (64,4 ft/s) sau hai giây, và cứ thế, tăng thêm 9,80665 m/s (32,1740 ft/s) mỗi giây. Nếu không có sức cản không khí, tất cả các vật thể từ cùng một độ cao sẽ chạm đất cùng một lúc.
Theo Định luật 3 của Newton, Trái Đất cũng phải chịu một lực bằng và ngược chiều với lực mà nó tác dụng lên vật rơi. Điều này có nghĩa là Trái Đất cũng bị kéo về phía vật thể cho đến khi chúng va chạm. Tuy nhiên, vì khối lượng của Trái Đất rất lớn, gia tốc của Trái Đất dưới lực này là không đáng kể so với vật thể. Nếu vật thể không nảy sau khi va chạm, thì lực tiếp xúc giữa vật thể và Trái Đất cân bằng với lực hấp dẫn, ngăn không cho gia tốc tiếp tục. Lực hấp dẫn trên Trái Đất là kết quả của hai lực: (a) Lực hấp dẫn theo định luật vạn vật hấp dẫn của Newton và (b) lực ly tâm do sự quay của Trái Đất. Lực hấp dẫn yếu nhất ở xích đạo do lực ly tâm và khoảng cách xa nhất từ tâm Trái Đất. Lực hấp dẫn thay đổi theo vĩ độ, tăng từ khoảng 9,780 m/s² ở xích đạo đến khoảng 9,832 m/s² ở hai cực.
Phương trình cho vật thể rơi tự do gần bề mặt Trái Đất
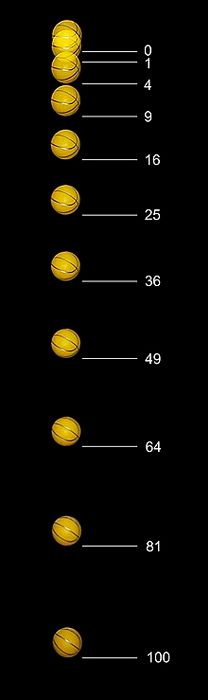
Dưới giả định lực hấp dẫn không thay đổi, định luật vạn vật hấp dẫn của Newton có thể đơn giản hóa thành F = mg, với m là khối lượng của vật thể và g là vectơ không đổi với cường độ trung bình 9,81 m/s² trên Trái Đất. Lực này xuất phát từ khối lượng của đối tượng và gia tốc do trọng lực được xác định bởi g. Một vật đứng yên và được thả rơi tự do dưới tác dụng của trọng lực sẽ di chuyển một khoảng cách tỷ lệ với bình phương của thời gian. Hình ảnh bên phải, kéo dài nửa giây, được ghi lại bằng đèn flash stroboscopic ở tốc độ 20 lần mỗi giây. Trong giây đầu tiên, vật di chuyển một đơn vị khoảng cách (khoảng 12 mm); và tiếp tục giảm 4 đơn vị, 9 đơn vị và cứ thế.
Theo giả định trọng lực không thay đổi, thế năng Ep của một vật thể ở độ cao h được tính bằng E p = mgh (hoặc Ep = Wh, với W là trọng lượng). Công thức này chỉ áp dụng cho các khoảng cách nhỏ h từ bề mặt Trái Đất. Tương tự, công thức chỉ có giá trị cho chiều cao tối đa đạt được của một vật thể ném thẳng đứng với vận tốc ban đầu v trong các trường hợp độ cao nhỏ và vận tốc ban đầu thấp.
Lực hấp dẫn và thiên văn học

Ứng dụng định luật hấp dẫn của Newton đã giúp chúng ta có được nhiều thông tin chi tiết về các hành tinh trong Hệ Mặt trời, khối lượng của Mặt trời và các quasar; thậm chí sự tồn tại của vật chất tối cũng được suy luận từ định luật này. Mặc dù chưa đến tất cả các hành tinh hay Mặt trời, nhưng chúng ta đã biết khối lượng của chúng thông qua định luật hấp dẫn và các đặc tính quỹ đạo đo được. Trong không gian, một vật thể duy trì quỹ đạo của nó nhờ lực hấp dẫn. Các hành tinh quay quanh các ngôi sao, các ngôi sao quay quanh các trung tâm thiên hà, và các thiên hà quay quanh một tâm khối lượng trong các cụm, với quỹ đạo của các cụm trong các siêu sao. Lực hấp dẫn giữa hai vật tỷ lệ thuận với tích khối lượng của chúng và tỷ lệ nghịch với bình phương khoảng cách giữa chúng.
Trọng lực ban đầu (có thể dưới dạng trọng lực lượng tử, siêu trọng lực hoặc một điểm kỳ dị hấp dẫn), cùng với không gian và thời gian, phát triển trong kỷ nguyên Planck (tối đa 10 giây sau khi vũ trụ hình thành), có thể từ một trạng thái nguyên thủy (như chân không giả, chân không lượng tử hoặc hạt ảo), theo một cách hiện chưa biết.
Sóng hấp dẫn

Theo thuyết tương đối rộng, năng lượng có thể được giải phóng khỏi hệ thống qua bức xạ hấp dẫn. Mọi vật thể đang tăng tốc có khả năng làm cong không-thời gian, từ đó bức xạ hấp dẫn được phát tán ra khỏi hệ thống. Các đối tượng như hệ Trái Đất-Mặt trời, cặp sao neutron, và cặp lỗ đen đều có thể tạo ra độ cong trong không-thời gian. Các hệ thống vật lý thiên văn khác, như các vụ nổ siêu tân tinh, cũng có thể mất năng lượng dưới dạng bức xạ hấp dẫn.
Bằng chứng gián tiếp đầu tiên về bức xạ hấp dẫn được cung cấp bởi các phép đo nhị phân của Hulse và Taylor vào năm 1973. Hệ sao này gồm một sao xung và một sao neutron quay quanh nhau. Thời gian quỹ đạo của chúng đã giảm kể từ khi phát hiện đầu tiên, điều này phù hợp với lượng năng lượng bị mất do bức xạ hấp dẫn. Nghiên cứu này đã được trao giải Nobel Vật lý năm 1993.
Bằng chứng trực tiếp đầu tiên về bức xạ hấp dẫn được phát hiện vào ngày 14 tháng 9 năm 2015 bởi các máy dò LIGO. Sóng hấp dẫn phát ra từ vụ va chạm của hai lỗ đen cách Trái Đất 1,3 tỷ năm ánh sáng đã được đo. Quan sát này xác nhận dự đoán lý thuyết của Einstein và các nhà khoa học khác rằng các sóng này thực sự tồn tại. Nó cũng mở ra cơ hội để quan sát và hiểu sâu hơn về lực hấp dẫn và các sự kiện vũ trụ, bao gồm cả Vụ nổ lớn. Các hiện tượng như sao neutron và sự hình thành lỗ đen cũng phát ra bức xạ hấp dẫn có thể đo được. Nghiên cứu này đã được trao giải Nobel Vật lý năm 2017.
Tốc độ của lực hấp dẫn
Vào tháng 12 năm 2012, một nhóm nghiên cứu từ Trung Quốc công bố rằng họ đã đo độ trễ pha của thủy triều Trái Đất trong các mặt trăng tròn và mới, dường như chứng minh rằng tốc độ của lực hấp dẫn bằng tốc độ ánh sáng. Điều này có nghĩa là nếu Mặt trời đột ngột biến mất, Trái Đất sẽ tiếp tục quay quanh nó bình thường trong 8 phút, khoảng thời gian ánh sáng cần để di chuyển quãng đường đó. Phát hiện này đã được công bố trong Bản tin Khoa học Trung Quốc vào tháng 2 năm 2013.
Vào tháng 10 năm 2017, các thiết bị LIGO và Virgo đã phát hiện tín hiệu sóng hấp dẫn đồng thời với các vệ tinh tia gamma và kính viễn vọng quang học từ cùng một hướng. Điều này xác nhận rằng tốc độ của sóng hấp dẫn tương đương với tốc độ ánh sáng.
Các bất thường và khác biệt
Có những quan sát chưa được giải thích đầy đủ, điều này có thể chỉ ra sự cần thiết của một lý thuyết lực hấp dẫn mới hoặc có thể được giải thích bằng các cách khác.
- Các ngôi sao cực nhanh: Trong các thiên hà, các ngôi sao ở vùng ngoại ô di chuyển nhanh hơn so với dự đoán của vật chất bình thường. Tương tự, các thiên hà trong cụm cũng cho thấy mô hình giống vậy. Vật chất tối, tương tác qua trọng lực nhưng không có điện từ, có thể giải thích cho sự khác biệt này. Các sửa đổi đối với động lực học Newton cũng đã được đề xuất.
- Sự bất thường của Flyby: Các tàu vũ trụ đã trải qua gia tốc lớn hơn mong đợi trong quá trình điều khiển trọng lực.
- Tăng tốc mở rộng: Sự mở rộng của không gian có vẻ đang gia tốc. Năng lượng tối được đề xuất để giải thích điều này. Một giải thích khác gần đây là hình học không đồng nhất của không gian (do các cụm thiên hà) và khi tính đến điều này, sự mở rộng không tăng tốc như dự đoán, tuy nhiên kết luận này vẫn còn tranh cãi.
- Sự gia tăng bất thường của đơn vị thiên văn: Các phép đo gần đây cho thấy quỹ đạo của các hành tinh đang mở rộng nhanh hơn nếu chỉ xét đến việc Mặt trời mất khối lượng bằng cách tỏa năng lượng.
- Các photon năng lượng bổ sung: Các photon đi qua các cụm thiên hà thu được năng lượng và sau đó mất đi khi ra ngoài. Sự giãn nở gia tốc của Vũ trụ ngăn các photon trả lại toàn bộ năng lượng, nhưng tính đến điều này từ các photon của bức xạ nền vi sóng vũ trụ cho thấy năng lượng thu được gấp đôi mong đợi. Điều này có thể chỉ ra rằng trọng lực giảm nhanh hơn bình phương nghịch đảo ở một khoảng cách nhất định.
- Các đám mây hydro cực lớn: Các vạch quang phổ của rừng Lyman-alpha cho thấy các đám mây hydro tập trung lại hơn dự kiến và, giống như dòng chảy tối, có thể chỉ ra rằng trọng lực giảm chậm hơn so với bình phương nghịch đảo ở một khoảng cách nhất định.
Các lý thuyết thay thế
Lý thuyết thay thế trong lịch sử
- Thuyết trọng lực của Aristote
- Lý thuyết hấp dẫn của Le Sage (1784), còn được gọi là lực hấp dẫn LeSage, được Georges-Louis Le Sage đề xuất, dựa trên giả thuyết một loại khí nhẹ lấp đầy toàn bộ Vũ trụ.
- Thuyết hấp dẫn của Ritz, Ann. Hóa. Vật lý. 13, 145, (1908) Trang. 267 Điện271, áp dụng động lực học Weber-Gauss cho trọng lực. Tiến bộ cổ điển của perihelia.
- Thuyết hấp dẫn của Nordström (1912, 1913), một trong những đối thủ đầu tiên của thuyết tương đối rộng.
- Lý thuyết Kaluza Klein (1921)
- Lý thuyết hấp dẫn của Whitehead (1922), một đối thủ cạnh tranh ban đầu khác của thuyết tương đối rộng.
Lý thuyết thay thế hiện đại
- Thuyết Brans-Dicke (1961) [51]
- Lực hấp dẫn cảm ứng (1967), một đề xuất của Andrei Sakharov cho rằng thuyết tương đối rộng có thể phát sinh từ các lý thuyết trường lượng tử của vật chất
- Lý thuyết dây (cuối thập niên 1960)
- (R) trọng lực (1970)
- Lý thuyết Horndeski (1974) [52]
- Siêu trọng lực (1976)
- Động lực học Newton đã sửa đổi (MOND) (1981), do Mordehai Milgrom đề xuất, sửa đổi định luật chuyển động thứ hai của Newton cho gia tốc nhỏ [53]
- Lý thuyết vũ trụ tự tạo của lực hấp dẫn (1982) của GA Barber, sửa đổi lý thuyết Brans-Dicke để cho phép tạo ra khối lượng lớn
- Trọng lực lượng tử vòng (1988) của Carlo Rovelli, Lee Smolin và Abhay Ashtekar
- Lý thuyết hấp dẫn không đối xứng (NGT) (1994) của John Moffat
- Trọng lực vô hướng vectơ (TeVeS) (2004), một sửa đổi tương đối tính của MOND của Jacob Bekenstein
- Thuyết Chameleon (2004) của Justin Khoury và Amanda Weltman.
- Lý thuyết Pressuron (2013) của Olivier Minazzoli và Aurélien Hees.
- Trọng lực phù hợp [54]
- Trọng lực như một lực entropic, coi trọng lực phát sinh như một hiện tượng xuất hiện từ khái niệm nhiệt động lực học của entropy.
- Trong lý thuyết chân không siêu lỏng, trọng lực và sự cong của thời gian không gian xuất hiện như một chế độ kích thích tập thể của siêu lỏng nền không tương đối.
