Trong toán học và nghệ thuật, hai đại lượng được gọi là có tỷ số vàng hoặc tỷ lệ vàng nếu tỷ lệ giữa tổng của hai đại lượng với đại lượng lớn hơn bằng tỷ lệ giữa đại lượng lớn hơn với đại lượng nhỏ hơn. Tỷ lệ vàng thường được ký hiệu bằng ký tự (phi) trong bảng chữ cái Hy Lạp, để tôn vinh Phidias, nhà điêu khắc xây dựng đền Parthenon.
Tỷ lệ vàng được biểu diễn như sau:
Phương trình này có nghiệm đại số là một số vô tỷ:
Tỉ lệ vàng có thể được đơn giản hóa thành 1:0,618.
Vào thời kỳ Phục Hưng, nhiều nghệ sĩ và kiến trúc sư đã thiết kế các tác phẩm của họ sao cho gần gũi với tỷ lệ vàng, đặc biệt là trong hình chữ nhật vàng, nơi tỷ lệ giữa cạnh dài và cạnh ngắn chính là tỷ lệ vàng. Các nhà toán học đã nghiên cứu tỷ lệ vàng vì sự độc đáo và những đặc tính thú vị của nó.
Lịch sử
Thời kỳ cổ đại
Nguồn gốc của tỉ lệ vàng vẫn còn là một bí ẩn. Trước đây, người ta cho rằng Vitruvius, một nhà toán học La Mã sống cách đây khoảng 2100 năm, đã phát hiện ra tỉ lệ vàng. Gần đây, các nhà khảo cổ học đã phát hiện các tài liệu liên quan đến tỉ lệ vàng trong các kim tự tháp Ai Cập, cho thấy tỉ lệ vàng đã xuất hiện từ rất lâu, khoảng hàng nghìn năm trước.
Euclid, nhà toán học vĩ đại, đã đề cập đến tỉ lệ vàng trong tác phẩm nổi tiếng của ông, 'Những nguyên tắc cơ bản.' Theo Euclid, điểm I trên đoạn AB được gọi là điểm chia đoạn AB theo tỉ lệ vàng (hay điểm vàng) nếu nó thỏa mãn điều kiện sau:
Đặt:. Giá trị x này chính là tỉ lệ vàng, và điểm I là điểm vàng trên đoạn AB.
Thời kỳ trung đại
Kể từ đó, đã có nhiều phát hiện về sự hiện diện của Tỷ Lệ Vàng trong các hình dạng hình học tự nhiên như hình sao 5 cánh và hình đa giác 10 cạnh, đặc biệt là trong chuỗi số Fibonacci.
Luca Pacioli (1445-1517) đã gọi tỷ lệ vàng là 'tỷ lệ thần thánh' trong tác phẩm Proportione Divina của mình.
Thế kỷ hiện đại
Mark Barr (thế kỷ 20) đã sử dụng ký hiệu chữ cái Hy Lạp phi (φ) để biểu thị tỷ lệ vàng.
Tính toán
| Nhị phân | 1.1001111000110111011... |
| Thập phân | 1.6180339887498948482... |
| Thập lục phân | 1.9E3779B97F4A7C15F39... |
| Đại số | |
| Chuỗi vô hạn |
Hai đại lượng a và b được xem là có tỷ số vàng φ nếu thỏa mãn điều kiện sau:
Bằng cách rút gọn phân số đầu tiên, ta có:
Ta có thể biến đổi phương trình bằng cách thay thế vào phương trình trên:
Khi nhân cả hai vế với φ, chúng ta có
Ta sắp xếp thành phương trình bậc hai như sau
Giá trị của φ sau khi giải phương trình bậc hai trên là
Nghiệm khác của phương trình bậc hai này là , tuy ít được biết đến hơn, nhưng cũng có những đặc điểm tương tự như φ.
Tỉ lệ vàng trong toán học
Tỷ lệ vàng là một số vô tỉ
Chứng minh: giả sử φ là một số hữu tỉ, nghĩa là là một số hữu tỉ, ta có thể chuyển đổi đẳng thức thành , vì φ là số hữu tỉ nên cũng phải là số hữu tỉ, nhưng lại là số vô tỉ, điều này mâu thuẫn với giả thuyết, nên φ phải là số vô tỉ.
Đa thức tối thiểu
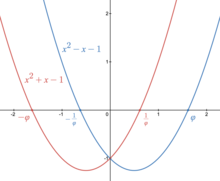
Tỷ lệ vàng đồng thời là một số đại số và cũng là số đại số nguyên. Đa thức tối tiểu của nó là:
Tỷ lệ vàng có liên hệ mật thiết với đa thức
Đa thức này có các nghiệm là và
Các thuộc tính khác
Số φ sở hữu hai đặc điểm nổi bật như sau:
Liên phân số và căn liên tiếp
Số φ có thể được biểu diễn dưới dạng liên phân số và căn liên tiếp như sau:
Ứng dụng của tỉ lệ vàng trong cuộc sống hàng ngày
Kiến trúc học

Các kỳ quan kiến trúc như kim tự tháp Khufu có tỷ lệ cạnh đáy và chiều cao gần bằng 62,66%, trong đó cạnh đáy dài 233m và chiều cao 146m; kim tự tháp Mikerinos có tỷ lệ 61,11%, với cạnh đáy dài 108m và chiều cao 66m. Dù có sự biến đổi qua thời gian, các công trình này vẫn gần với tỷ lệ vàng. Tháp Eiffel có tỷ lệ khoảng 61,36%, với chiều cao phần thân chính là 184,8m và chiều ngang là 300,5m.
Tháp Rùa tại Việt Nam cũng được cho là mang dấu ấn của tỷ lệ vàng.
Những tỉ lệ cơ thể con người


Tỉ lệ vàng hiện diện trong các kích thước cơ thể con người, chẳng hạn như tỷ lệ giữa chiều cao rốn, chiều cao toàn thân, chiều dài cẳng tay, và chiều dài cánh tay,...
Nếu cơ thể bạn đạt được những tỷ lệ sau đây, bạn sẽ có hình dáng rất cân đối và hấp dẫn:
- Tỷ lệ giữa chiều cao và khoảng cách từ đỉnh đầu đến đầu ngón tay bằng
- Tỷ lệ giữa khoảng cách từ đỉnh đầu đến đầu ngón tay và khoảng cách từ đỉnh đầu đến rốn (hoặc cùi chỏ) là
- Tỷ lệ giữa khoảng cách từ đỉnh đầu đến rốn (hoặc cùi chỏ) và khoảng cách từ đỉnh đầu đến ngực là
- Tỷ lệ giữa khoảng cách từ đỉnh đầu đến rốn (hoặc cùi chỏ) và chiều rộng đôi vai là
- Tỷ lệ giữa khoảng cách từ đỉnh đầu đến rốn (hoặc cùi chỏ) và chiều dài cẳng tay là
- Tỷ lệ giữa khoảng cách từ đỉnh đầu đến rốn (hoặc cùi chỏ) và chiều dài xương ống quyển là
- Tỷ lệ giữa khoảng cách từ đỉnh đầu đến ngực và khoảng cách từ đỉnh đầu đến gốc sọ là
- Tỷ lệ giữa khoảng cách từ đỉnh đầu đến ngực và chiều rộng của bụng là
- Tỷ lệ giữa chiều dài của cẳng tay và chiều dài bàn tay là
- Tỷ lệ giữa khoảng cách từ vai đến các đầu ngón tay và từ khuỷu tay đến các đầu ngón tay là
- Tỷ lệ giữa khoảng cách từ hông đến mặt đất và từ đầu gối đến mặt đất là
- Đặt độ dài từ rốn đến đỉnh đầu là x và độ dài từ rốn đến chân là y. Nếu độ dài một cánh tay là a, và tỉ lệ x/y = a/(x+y) = 1/φ = Ф = 0.618033..., thì đó là hình thể của các siêu mẫu lý tưởng.
Trong lĩnh vực tôn giáo
Hà Đồ, Lạc Thư và Bát Quái là ba sơ đồ cổ xưa, có nguồn gốc từ các bộ lạc phía Nam sông Dương Tử (nơi khởi nguồn của người Việt cổ). Mỗi sơ đồ đã được truyền bá và sử dụng cho nhiều mục đích khác nhau.
Phục Hy đã dựa vào Hà Đồ để phát triển Tiên thiên Bát quái, trong khi Chu Văn Vương căn cứ vào Lạc Thư để xây dựng Hậu thiên Bát quái. Những sơ đồ này chứa đựng tri thức của người xưa về vũ trụ.
Trong Phật giáo, ký hiệu chữ Vạn tượng trưng cho lòng từ bi. Đạo giáo có biểu tượng Thái cực, còn Dịch học có Bát quái.
Tuy nhiên, đây chưa phải là toàn bộ. Văn hóa phương Đông chủ yếu có Đạo gia và Phật gia. Đạo gia dùng biểu tượng Thái Cực, trong khi Phật gia dùng chữ Vạn (卍). Những biểu tượng này đều phản ánh quan niệm vũ trụ của hai trường phái này và có liên quan đến Hà Đồ và Lạc Thư.
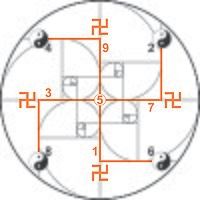
Lạc Thư được cấu thành từ các số lẻ (tổng số là 9), trong đó ẩn chứa biểu tượng chữ Vạn (卍); Ngược lại, Hà Đồ bao gồm các số chẵn (tổng số là 10), chứa biểu tượng Thái Cực. Như vậy, chữ Vạn (卍) đại diện cho số lẻ, và Thái Cực đại diện cho số chẵn.
Thay số lẻ bằng chữ Vạn (卍) và số chẵn bằng Thái Cực để tạo thành một ma trận.
